费马(分割)定理及其推广

北京市首都师范大学附属回龙观育新学校(102208) 牛文政

北京市昌平区大东流中学(102211) 王素文

三百多年前费马(Pierre de Fermat，1601-1665)提出了一个这样的问题：

费马(分割) 定理如图1， 矩形ABCD 的边长AB :以AB 为直径在矩形外作半圆，在半圆上任取一点P，连结PC,PD 分别交AB于E,F，那么AE2+BF2=AB2.

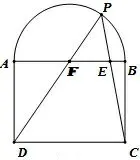
图1

费马提出这个问题后，欧拉(Euler，1707－1783)、西姆松首先完成证明.

1.文献综述

R·A·Johnson 先生在文[l]中给出了一个漂亮的“福地法”证明，尚强先生在文[2]中给出一个代数证法，较冗长繁杂.文[3]对文[2]的代数证法进行改进，使其较原证法简洁易懂.文[4]在文[3]的基础上，给出了更简捷的代数证明.

文[5]用代数配合几何的方法给出了引申1，并用几何画板验证了引申2：

引申1ABCD 是任意矩形，以AB 为直径在矩形外作半圆，在半圆上任取一点P，连结PC,PD 分别交AB 于E、F，那么

引申2如图2，3，4，矩形ABCD 的边长AB :AD =2，以AB 为直径在矩形内作半圆，在半圆上任取一点P，连结PC,PD 分别交AB 于E、F，那么AE2+BF2=AB2.

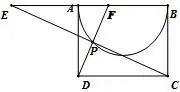
图2

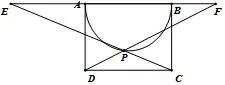
图3

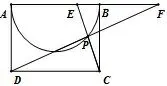
图4

文[4]的改进很有意义，基本上明确了这个问题的代数结构.文[5]的研究是先从几何方法入手，转向代数方法，从代数上给出了为何费马(分割)定理中矩形边长之比是不过，文[5]的作者没有意识到，在引申1 中，对任意的矩形ABCD，若以AB 为直径在矩形内作半圆，引申1 的结论是可以由文[1]的前文直接证明，其过程字母都不用变，只是图形的位置有所变化(可参照图2，3，4)，而用几何画板只能进行验证.

文[6]的代数配合几何证法，相当于文[5]的引申1 的证明.而相对于文[6]来说，文[7]的简证相对简单些，却使人“仍感证明过程不太简明”[8].文[8-9]的平面几何证法主要运用相似与比例性质证明，相对简明些，却失去了费马分割定理的本质，不如文[3-5]中的代数方法深刻.

文[6]的解析几何证法，由于没有注意到图形的对称性，所以略显冗繁.文[8-9]的解析证法基本一致，都是设点E、F的坐标，用三点共线整体代入证明的，这种证明实际上也是脱胎于文[3-5]的代数方法.

在文[3-9]的对费马(分割)定理的证明与引申中，有用平面几何方法的，有用代数方法解决的，还有两者结合的，我们仿佛看到： 这个问题的解决过程，有从传统的欧氏几何方向向解析几何方向过渡的影子.那么，作为解析几何的创始人之一的费马，是用什么方法得到这个定理的呢?

和R.笛卡尔同时或较早，费马已得到解析几何的要旨.他在《平面与立体轨迹引论》(开始于1629年，1636年前完成;“立体轨迹”指不能用尺规作出的曲线，与现在的含义不同)一文中明确指出方程可以描述曲线，并通过方程的研究推断曲线的性质.因此，他和笛卡尔分享创立解析几何的荣誉.被誉为“业余数学家之王的”费马虽年近三十才认真注意数学，但成果累累.他性情淡泊，为人谦逊，对著作无意发表.去世后，很多论述遗留在旧纸堆里，或书页的空白处，或在给朋友的书信中.他儿子的S.费马将这些汇集成书，共两卷，在图卢兹出版(1679年).包括最有名的“费马大定理”及本定理等等在内，由于后来找不到费马的证明，后人才陆续地补上相关的证明.[10]由于费马是解析几何的创始人之一，因此，我们有理由猜想，费马是应用解析几何方法来证明这个问题的.

2.费马(分割)定理的推广

由于圆可以看成是特殊的椭圆，本文将对此问题进行推广，并采用解析几何的方法来解决.

问题1如图5，6，7，8，四边形ABCD 为矩形，在以AB为椭圆的一个轴(长轴或短轴)的椭圆(或以AB 为直径的圆)上任取一点P， 直线PC,PD 分别交直线AB 于E,F，如果AE2+BF2= λAB2(λ ＞0).那么矩形ABCD 的边长AB :AD 为何值?

图5

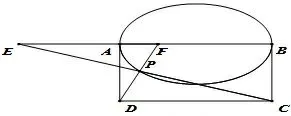
图6

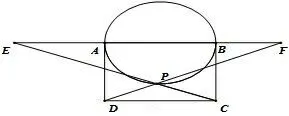
图7

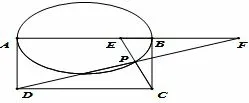
图8

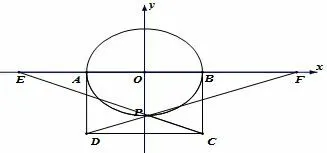
图9

分析以AB 的中点O 坐标原点， AB 为x 轴， 建立直角坐标系(如图9)， 为了使问题具有一般性， 设曲线Γ 的方程为则有A(-m,0)， B(m,0)，显然， 当m = n ＞0 时， 椭圆退化为圆.设C(m,-km)，D(-m,-km)，其中k ＞0，则有设F (x1,0)，E(x2,0)，P (x0,y0)，因为点P 在曲线Γ 上，所以(x0+m,y0+km)，(x0-x1)(y0+km) =(y0+km0)， 由对称性，有所以

如果AE2+ BF2= λAB2= 4λm2， 那么， 对任意的y0∈[-n,n]，都有：

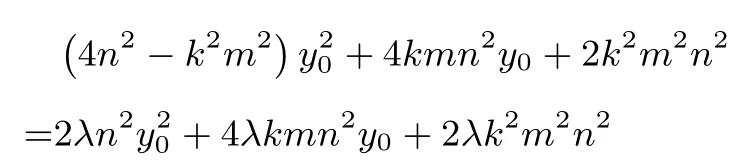
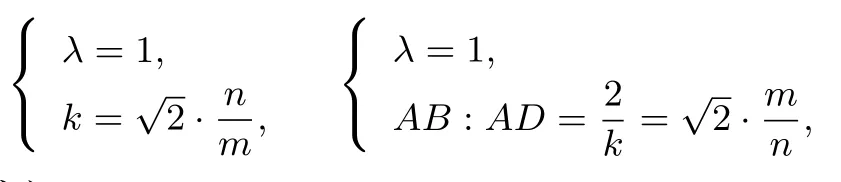
恒成立.

于是，我们得到：

椭圆(或圆)分割定理矩形ABCD 的边长AB :AD =在以AB 为椭圆的一个轴(长轴或短轴，长为m;另一个轴长为n;当m = n ＞0 时，椭圆退化为圆)的椭圆(或圆)上任取一点P， 直线PC,PD 分别交直线AB 于E,F，那么AE2+BF2=AB2.

椭圆(或圆) 分割逆定理四边形ABCD 为矩形， 在以AB 为椭圆的一个轴(长轴或短轴， 长为m; 另一个轴长为n; 当m = n 时， 椭圆退化为圆) 的椭圆(或圆)上任取一点P， 直线PC,PD 分别交直线AB 于E,F，如果AE2+ BF2= AB2， 则有矩形ABCD 的边长

文[5]的引申2 及文[7]的引申是上述定理的特例.关于这个两个定理是否可以推广到双曲线与抛物线的情形，这里留给读者思考.

问题2对于文[5]的引申1，将圆变成椭圆，结论是否依然成立呢?

分析对于任意矩形ABCD，由问题1 的分析，知

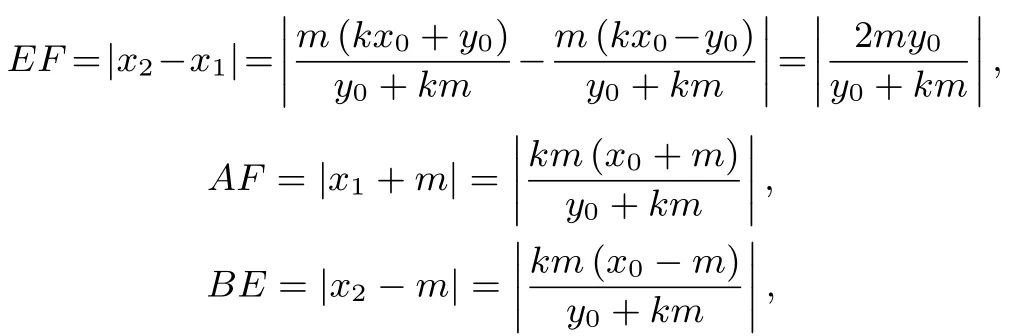
于是，我们得到：

椭圆(或圆) 分割比例定理四边形ABCD 是任意矩形，在以AB 为椭圆的一个轴(长轴或短轴，长为m;另一个轴长为n; 当m = n ＞0 时， 椭圆退化为圆)的椭圆(或圆)上任取一点P，直线PC,PD 分别交直线AB 于E,F，那么

椭圆(或圆) 分割比例理逆定理四边形ABCD 是矩形，在以AB 为椭圆的一个轴(长轴或短轴，长为m;另一个轴长为n; 当m = n ＞0 时， 椭圆退化为圆)的椭圆(或圆)上任取一点P，直线PC,PD 分别交直线AB 于E,F，如果那么

在这里我们溯本回源，运用费马与R.笛卡尔创立的解析几何思想方法，将费马(分割)推广并证明，再一次体会了解析几何的用代数方法来解决几何问题的魅力.

我们换一个角度来看这个问题.将椭圆在y 轴方向“拉长”(或“缩短”)到倍得到圆x2+y2= m2，根据圆中的费马(分割)定理成立的条件，再按比例在y 轴方向“缩短”(或“拉长”)回去，就得到了椭圆分割定理.研究图形在变换中有哪些性质不变，研究保持性质不变的所有那些变换，这是著名数学家克莱茵在著名的“爱尔兰根纲领”中所阐述的几何学最重要的思想.以上利用“伸缩变换”将圆与椭圆相互转化，就是利用“爱尔兰根纲领”的数学思想解决问题的一个例子.