Nonlinear Degenerate Anisotropic Elliptic Equations with Variable Exponents and L1 Data

KHELIFI Hichemand MOKHTARI Fares

1Department of Mathematics and Informatics,University of Algiers,Algiers,Algeria.2 Street Didouche Mourad Algiers.

2Applied Mathematics Laboratory,Badji Mokhtar University-Annaba B.P.12,Algeria.

Abstract.This paper is devoted to the study of a nonlinear anisotropic elliptic equation with degenerate coercivity,lower order term and L1 datum in appropriate anisotropic variable exponents Sobolev spaces. We obtain the existence of distributional solutions.

Key Words:Sobolev spaces with variable exponents;anisotropic equations;elliptic equations;L1 data.

1 Introduction

In this paper we prove the existence of solutions to the nonlinear anisotropic degenerate elliptic equations with variable exponents,of the type

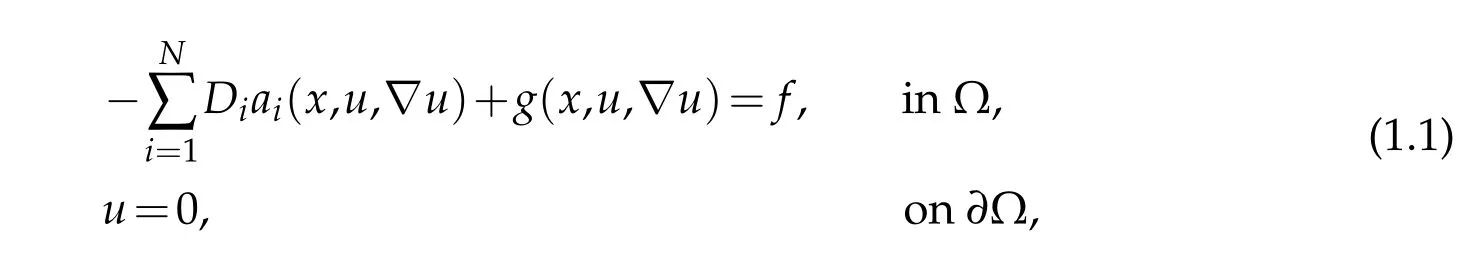
where Ω⊆RN(N ≥3)is a bounded domain with smooth boundary∂Ω and the righthan d sidefinL1(Ω),We suppose thatai:Ω×R×RN →R,i=1,...,Nare Carathéodory functions such that for almost everyxin Ω and for every(σ,ξ)∈R×RNthe following assumptions are satisfied for alli=1,...,N

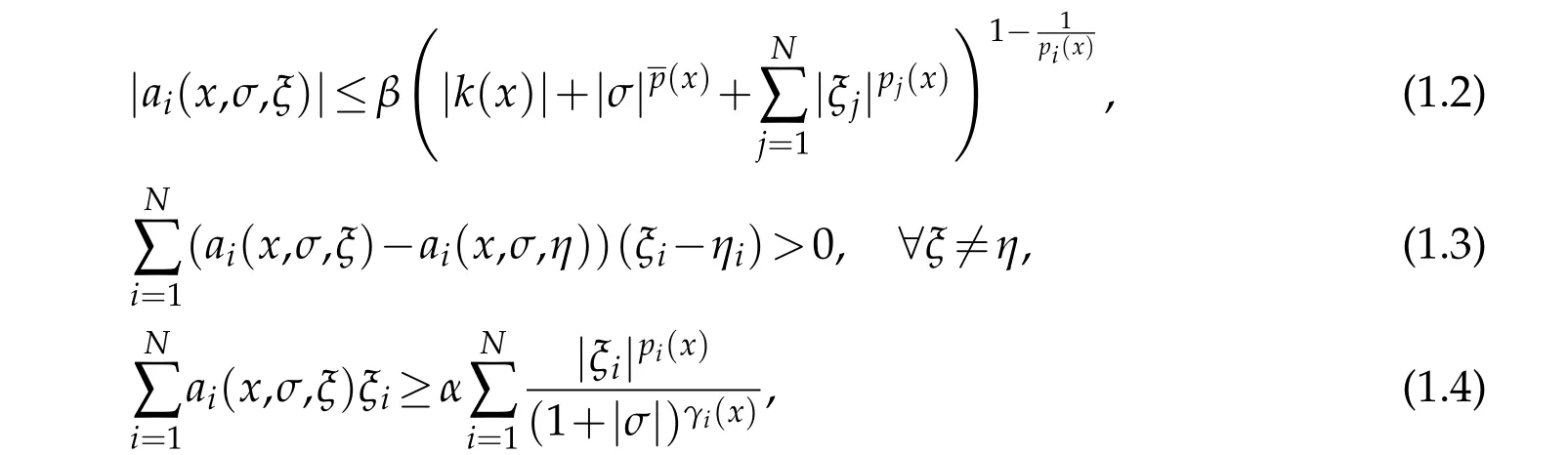
whereβ ＞0,α ＞0,and(1,+∞)are continuous functions andis such that

We introduce the function

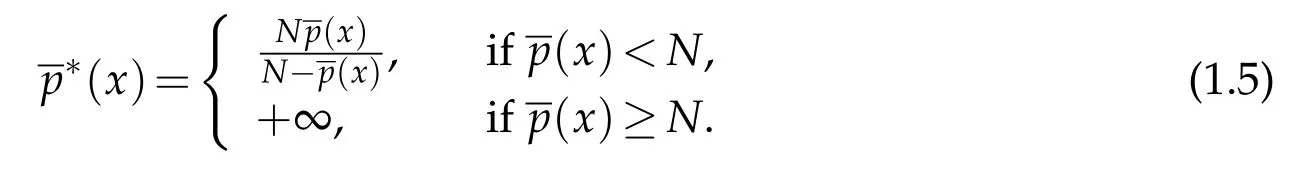
The nonlinear termg:Ω×R×RN →R is a Carathéodory function such that for a.e.x∈Ω and all(σ,ξ)∈R×RN,we have

whereb:R+→R+is a continuous and increasing function with finite values,c ∈L1(Ω)and∃ρ＞0 such that:

In[1],the authors obtain the existence of renormalized and entropy solutions for the nonlinear elliptic equation with degenerate coercivity of the type

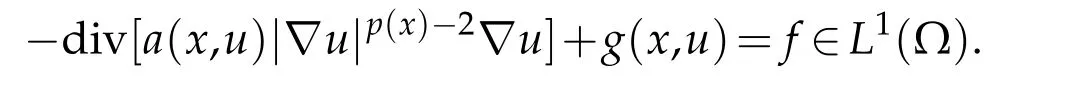
Forg ≡0 andf ∈Lm(·)(Ω),withm(x)≥m-≥1,equation of the from(1.1)have been widely studied in[2],where the authors obtain some existence and regularity results for the solutions.Ifg≡|u|s(x)-1u,

andf ∈Lm(Ω),withm ≥1,existence and regularity results of distributional solutions have been proved in[3].

As far as the existence results for our problem(1.1)there are three difficulties associated with this kind of problems.Firstly,from hypothesis(1.2),the operator

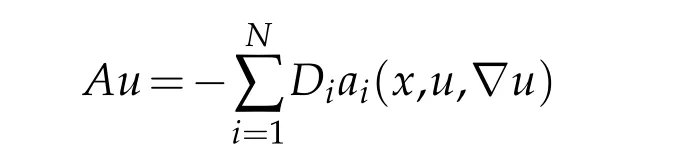
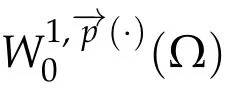
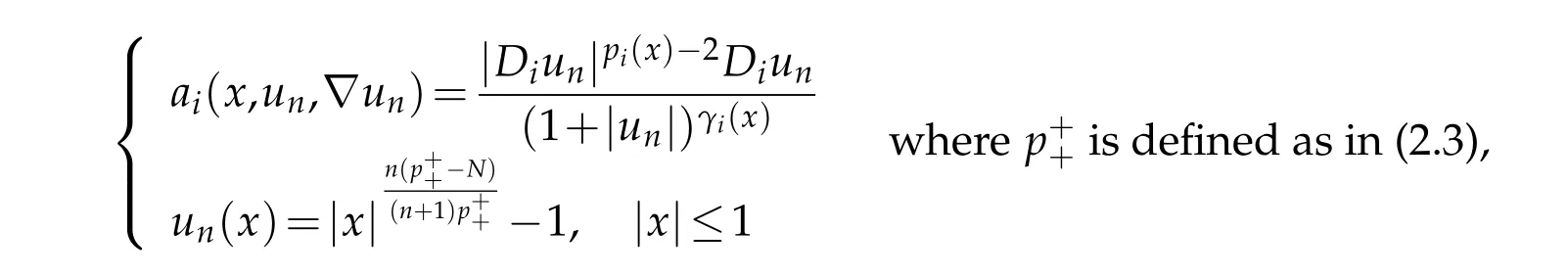
the operatorAis not coercive.Because,iftends to infinity then

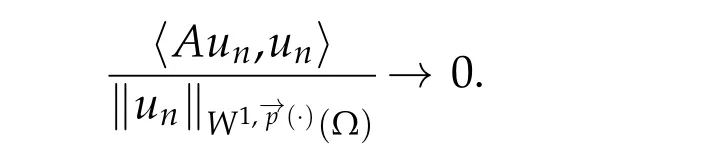
So,the classical methods used in order to prove the existence of a solution for(1.1)cannot be applied. The second difficulty is represented in the fact thatg(x,u,∇u)can not be defined frominto its dual,but fromintoL1(Ω). The third difficulty appears when we give a variable exponential growth condition(1.2)forai. The operatorApossesses more complicated nonlinearities;thus,some techniques used in the constant exponent case cannot be carried out for the variable exponent case.For more recent results for elliptic and parabolic case,see the papers[4–8]and references therein.

The paper is organized as follows.In Section 2,we present results on the Lebesgue and Sobolev spaces with variable exponents both for the isotropic and the anisotropic cases,and state the main results.The proof of the main result will be presented in Section 3.We start by giving an existence result for an approximate problem associated with(1.1).The second part of Section 3 is devoted to proving the main existence result by using a priori estimates and then passing to the limit in the approximate problem.

2 Preliminaries and statement of the main result

2.1 Preliminaries

In this sub-section,we recall some facts on anisotropic spaces with variable exponents and we give some of their properties.For further details on the Lebesgue-Sobolev spaces with variable exponents,we refer to[9–11]and references therein.Let Ω be a bounded open subset of RN(N ≥2),we denote

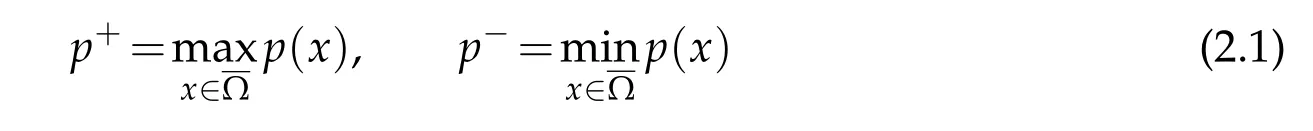
and

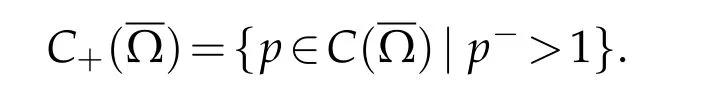
LetWe define the space

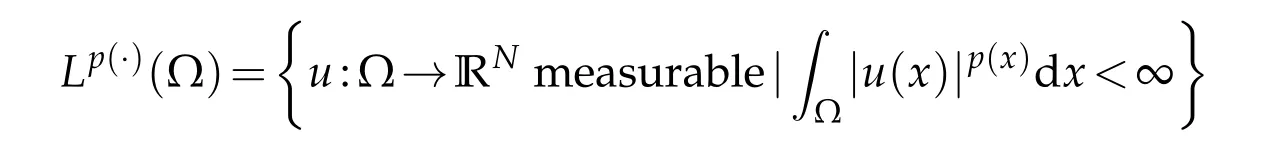
then the expression

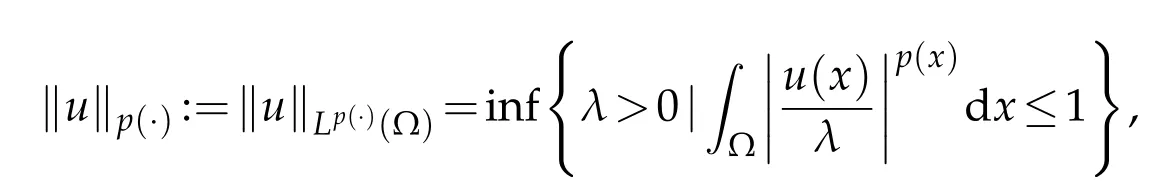
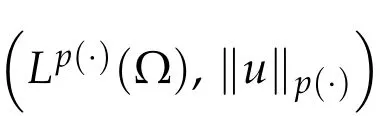
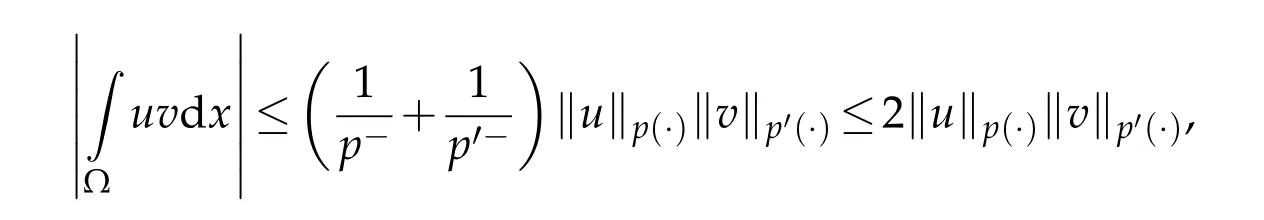
holds true.We define the variable exponents Sobolev spaces by

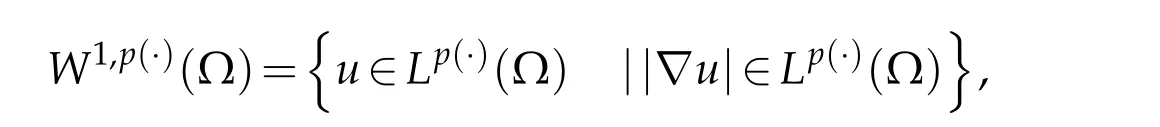
which is a Banach space equipped with the following norm

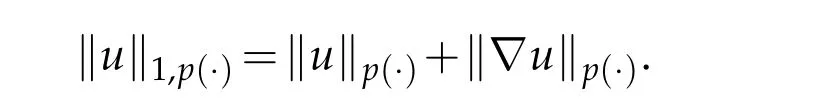
Next,we defineas the closure ofinW1,p(·)(Ω). Finally,we introduce a natural generalization of the variable exponents Sobolev spacesthat will enable us to study with sufficient accuracy problem(1.1).Letwhereare continuous functions.We introduce the anisotropic variable exponents Sobolev spaces

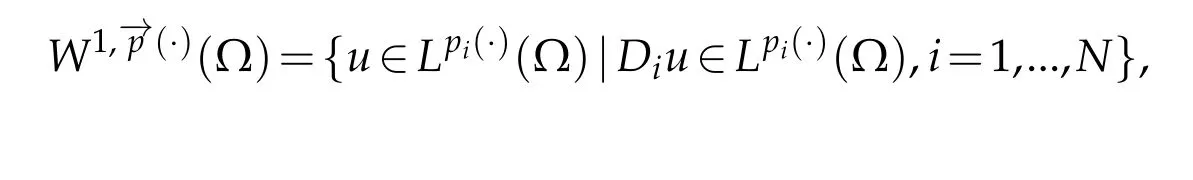
with respect to the norm

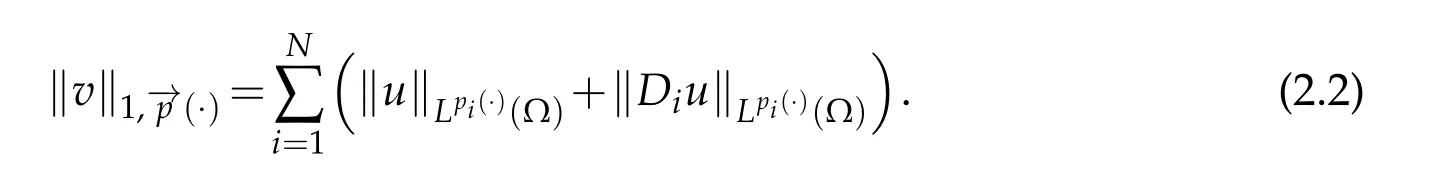
We introduce the following notationas

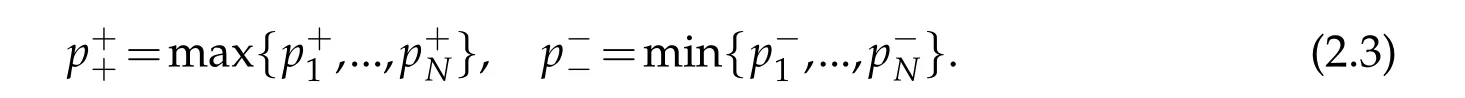
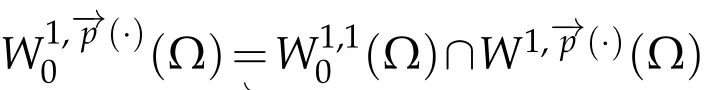
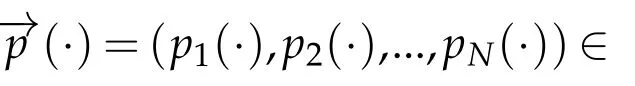
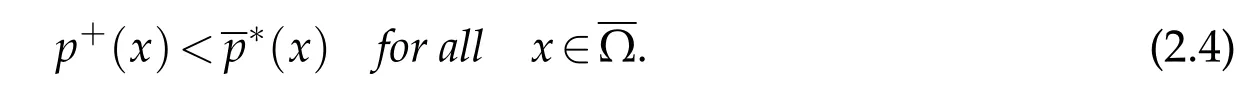
Then

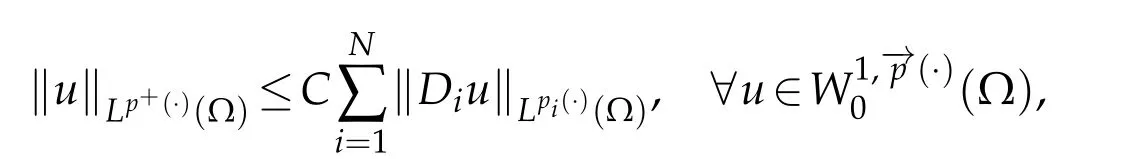
where p+is defined as in(2.1)(1.5),and C is a positive constant independent of u.Thusis an equivalent norm on

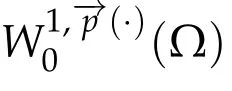
Proof.Put

Thanks to(Proposition 2.1 in[3]),we have

Using the convexity of the applicationwe obtain

We will use through the paper,the truncation functionTkat heightk(k ＞0),that isTk(s):=max{-k,min{k,s}}.

Lemma 2.1([12]).Let g∈Lp(·)(Ω)and gn∈Lp(·)(Ω)with‖gn‖p(·)≤C.If gn(x)→g(x)almost everywhere inΩ,then gn ⇀g in Lp(·)(Ω).

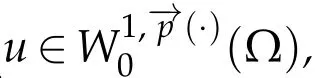
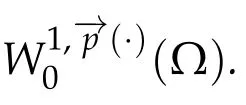
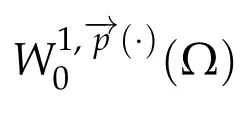
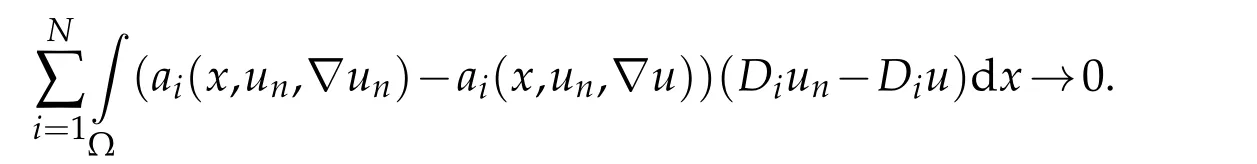
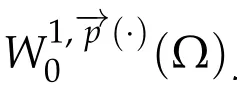
2.2 Statement of main result

We will extend the notion of distributional solution,see[12,13],to problem(1.1)as follows:

Definition 2.1.Let f ∈L1(Ω)a measurable function u is said to be solution in the sense of distributions to the problem(1.1),if

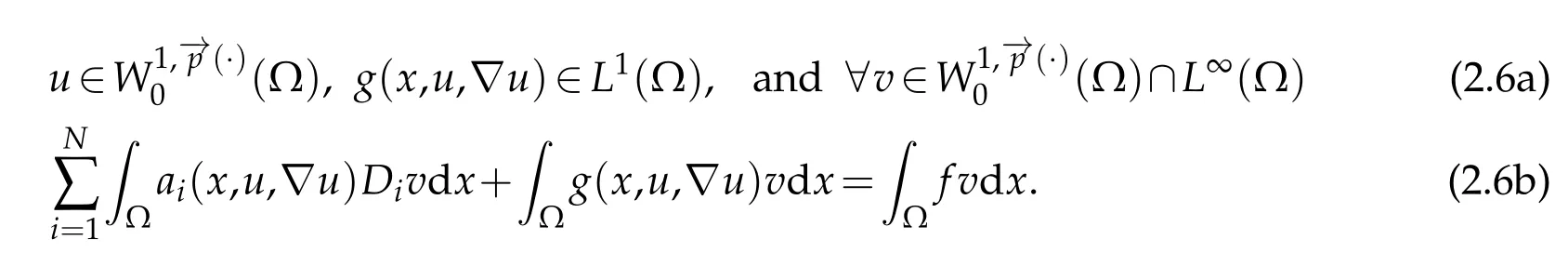
Our main result is as follows

Theorem 2.2.Let f ∈L1(Ω).Assume(1.2)-(1.8)and(2.4).Then problem(1.1)has at least one solution in the sense of distributions.

3 Proof of the main result

3.1 Approximate solution

Let(fn)nbe a sequence inL∞(Ω)such thatfn →finL1(Ω)with|fn|≤|f|(for examplefn=Tn(f))and we consider the approximate problem

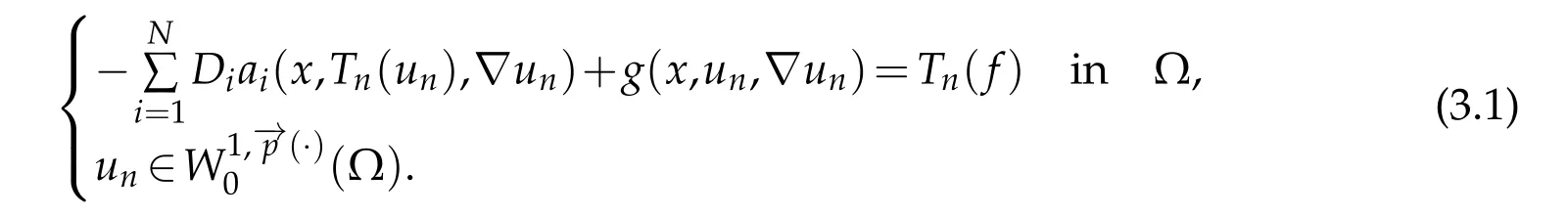
Lemma 3.1.Let f ∈L1(Ω).Assume(1.2)-(1.8)and(2.4).Then,problem(3.1)has at least one solution in the sense of distributions.

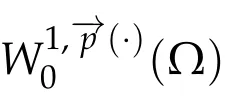
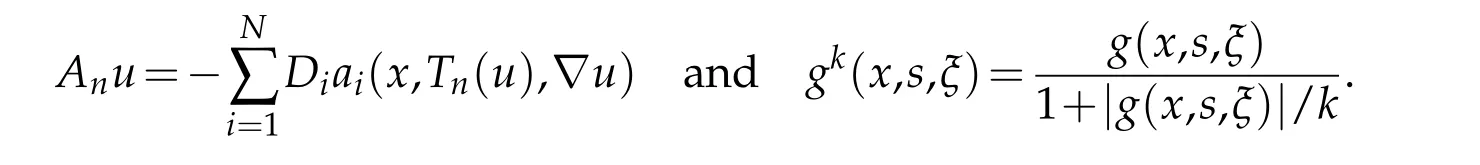
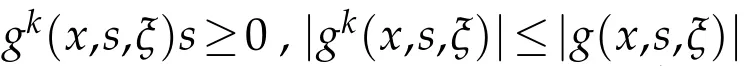
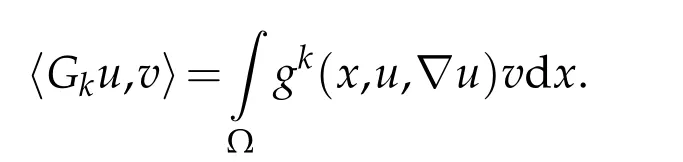
Consider the following problem

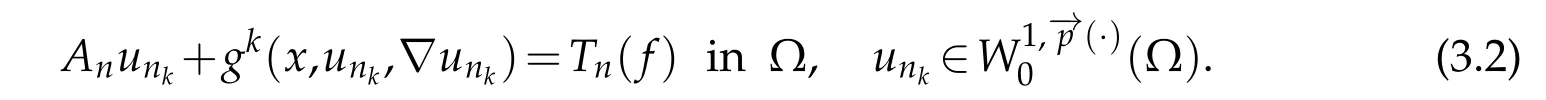
Lemma 3.2.Let f ∈L1(Ω).Assume that(1.2)-(1.8)and(2.4)hold,then the problem(3.2)has at least one solution unk in the sense of distributions.

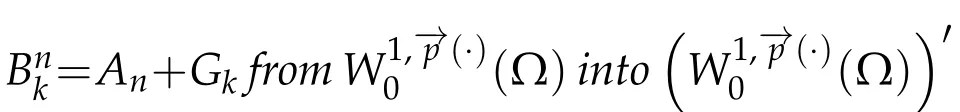
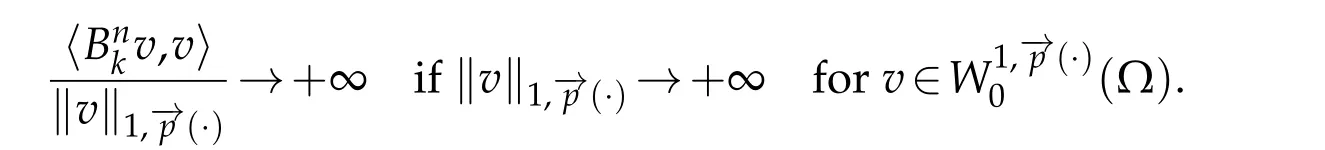
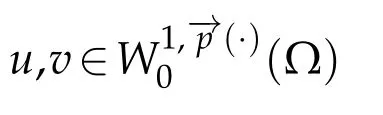
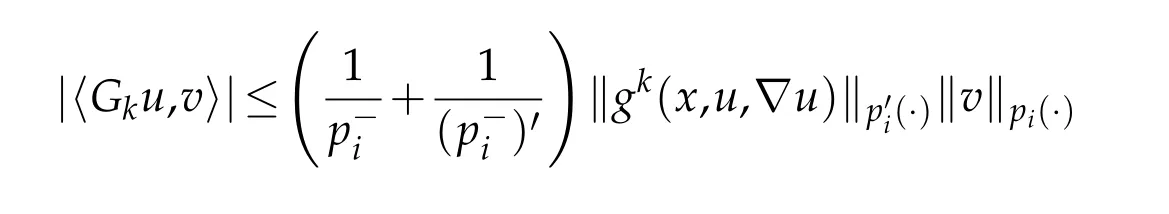
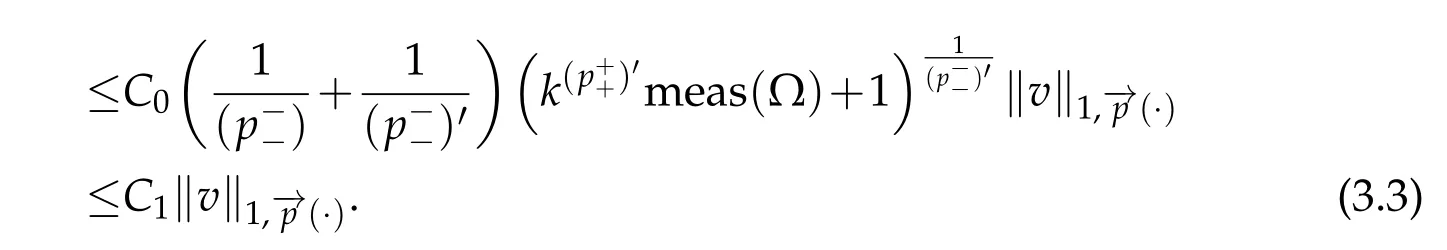
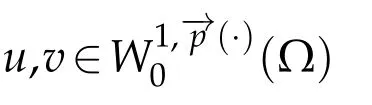
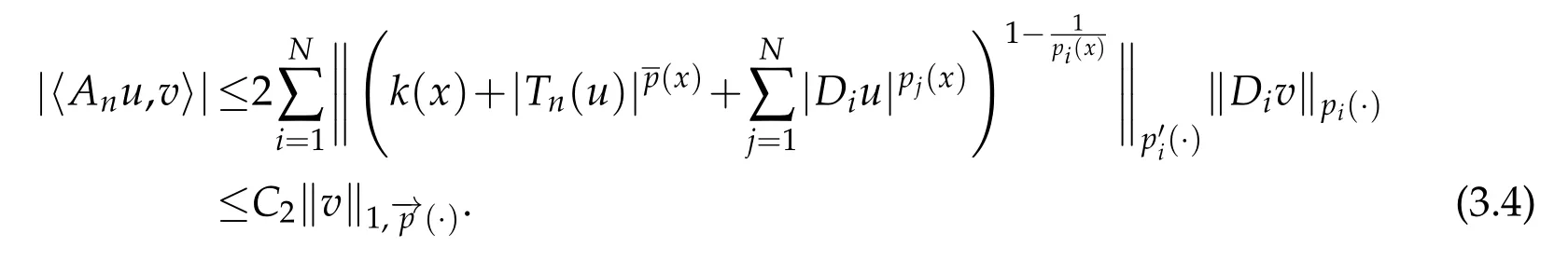
Then by using(3.3)and(3.4)we conclude thatis bounded.For the coercivity,by using(1.4),(1.7),and(2.5),we get

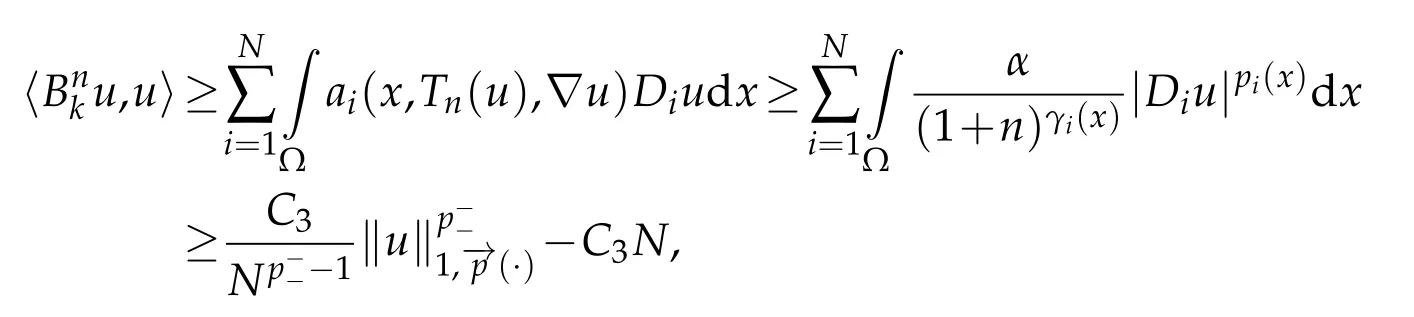
then

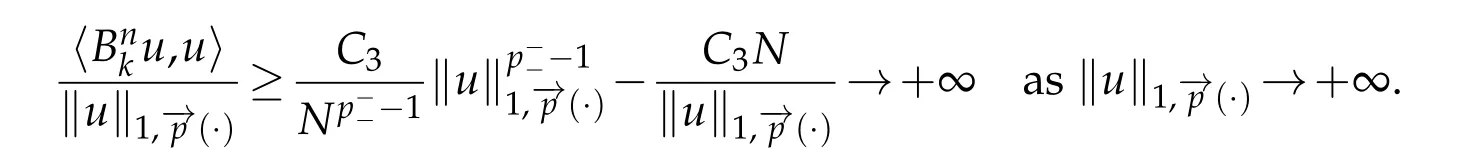
It remains to show thatis pseudo-monotone.Let(um)mbe a sequence insuch that

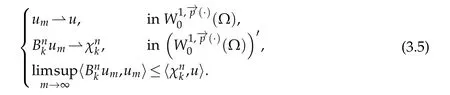
We will prove that

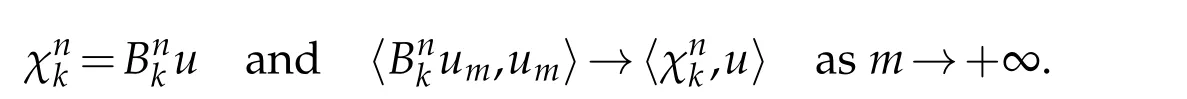
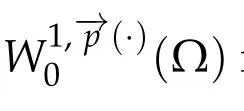
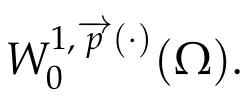
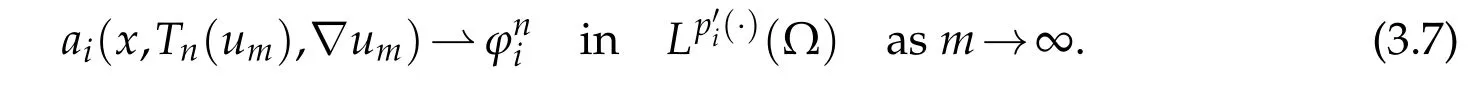
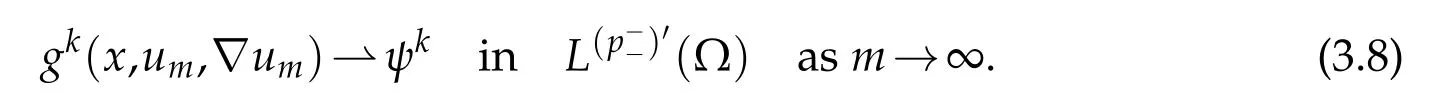
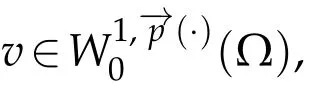
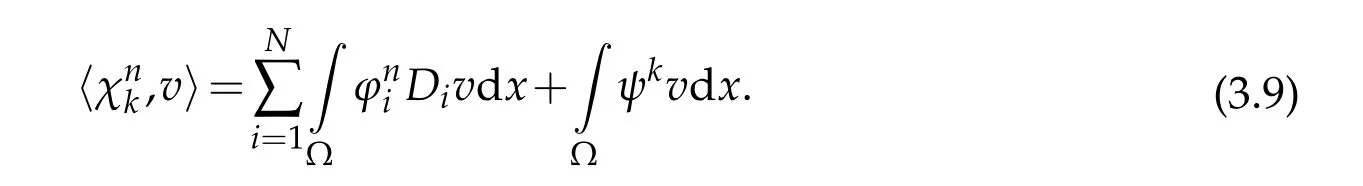
Using(3.5),(3.8),(3.9),and thatum →uinwe have

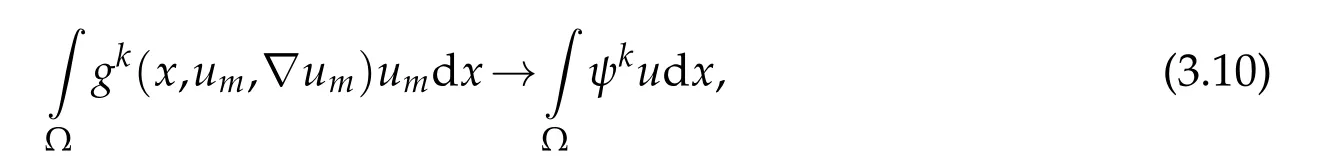
therefore,thanks to(3.5),(3.9),and(3.10),we write

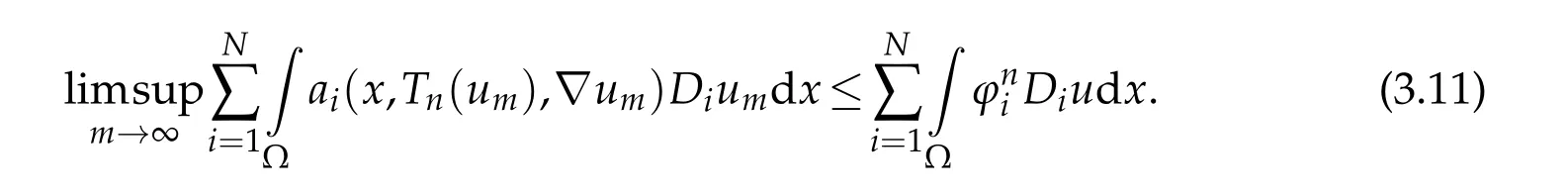
On the other hand,by(1.3),we obtain

在刑事诉讼过程中，检察机关天生拥有比被告人更为强大的公诉权，处于绝对的优势地位。如果检察机关的这种天生的权力不受到外部程序控制的话很容易被滥用。庭前会议制度拥有对公诉权进行司法审查与控制的功能，能够有效地防止检察机关滥用公诉权，可以把一些不符合起诉条件的案件排除在审判程序之外，对进入审判程序的案件起到一个筛选和过滤的功能。

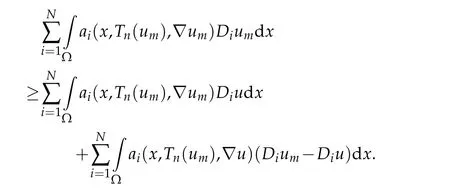
In view of Lebesgue dominated convergence theorem and(3.6),we have

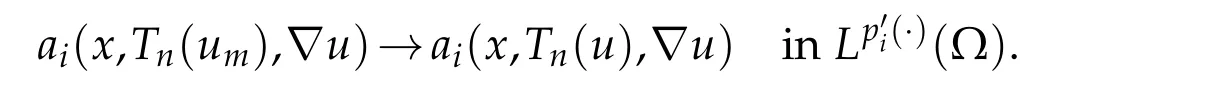
By(3.7)and(3.5),we get

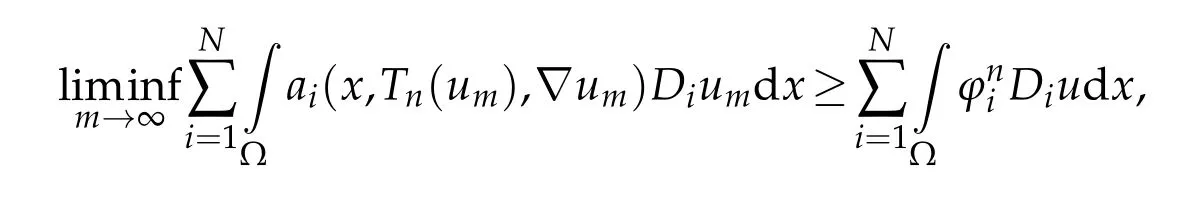
this implies,thanks to(3.11),that

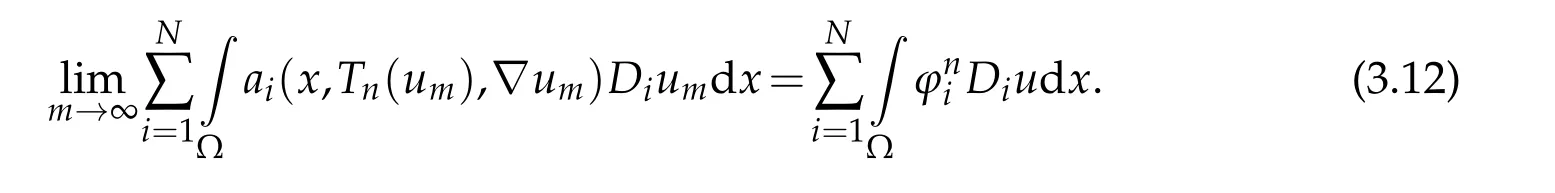
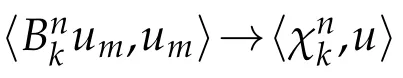
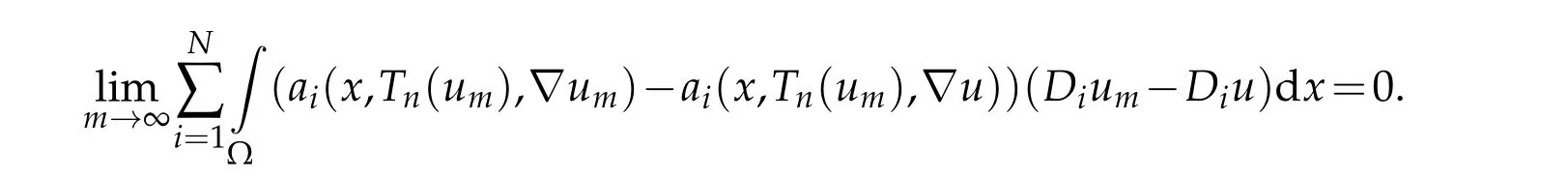
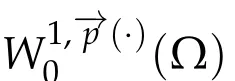
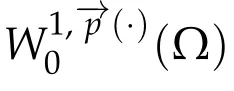
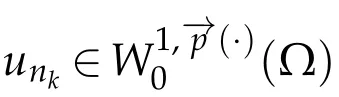
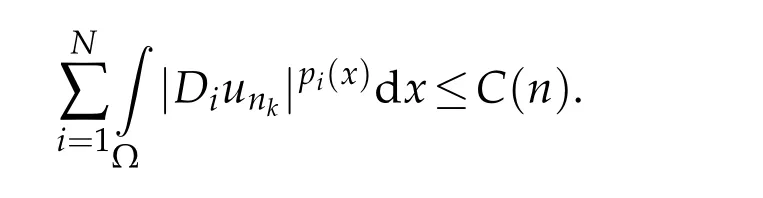
Proof.The proof uses the same technique as in(Lemma 4.1 of[3])and is omited here.

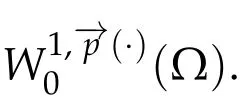
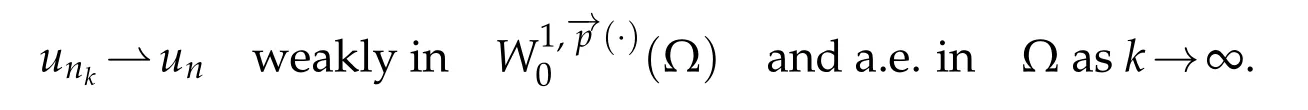
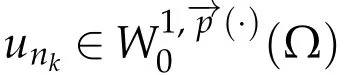
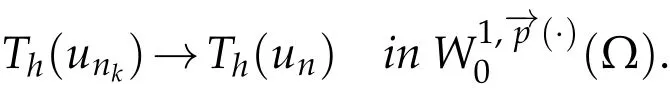
Proof.It is similar to the proof of Theorem 4.2 of[13].

3.2 A priori estimates

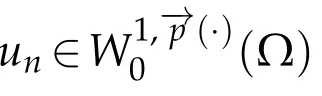
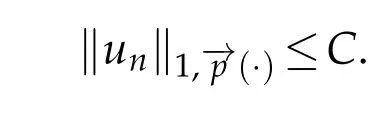
Proof.Leth＞0.TakingTh(un)as a test function in(3.1),then

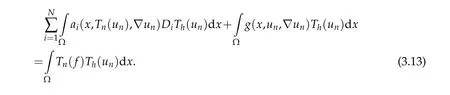
By dropping the nonnegative term in(3.13),(1.7),and(1.4)we get

then

Consequently,

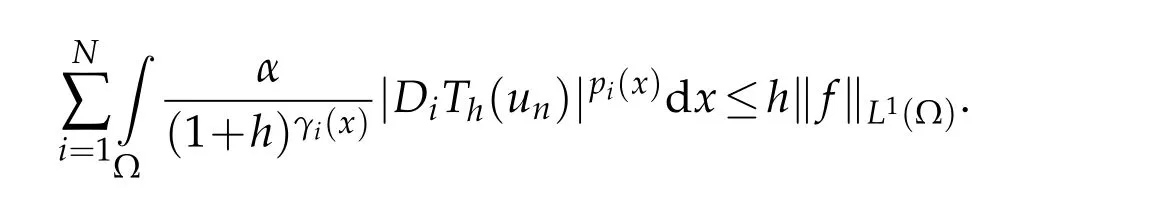
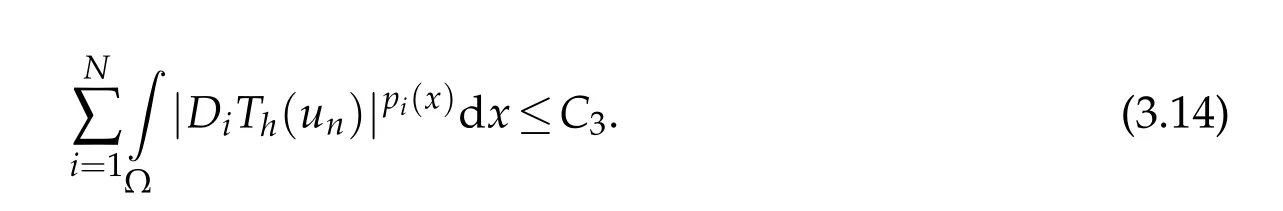
TakingTh(un)as a test function in(3.1),and dropping the first nonnegative term in the left-hand side,we obtain

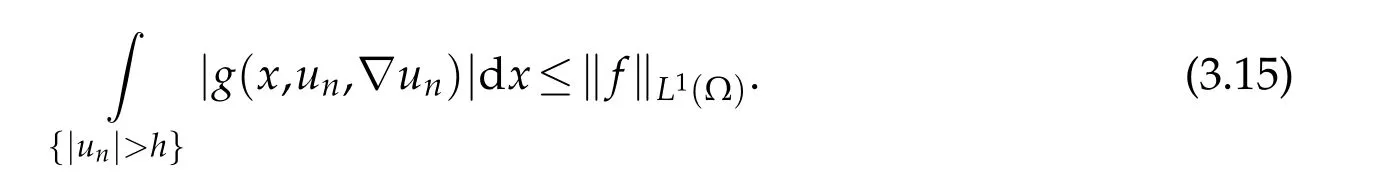
By combining(1.8),(3.14)and(3.15),forh=ρ,we deduce that

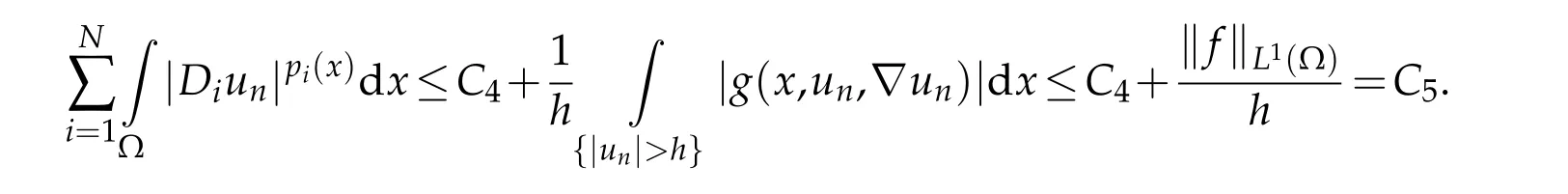
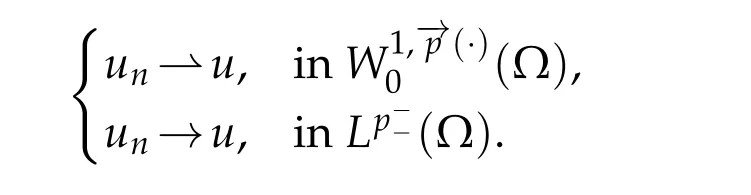
This ends the proof of Lemma 3.6.

3.3 The strong convergence of the truncation

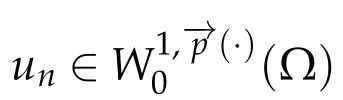
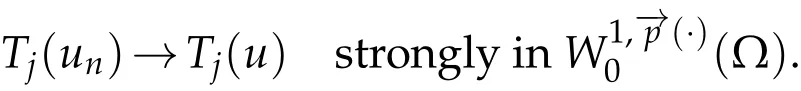
Proof.Leth ≥j ＞0 andwn=T2j(un-Th(un)+Tj(un)-Tj(u)).We setφj(s)=s·exp(δs2),whereδ=(l(j)/(2α))2,l(j)=b(j)(1+|j|)γ++,and

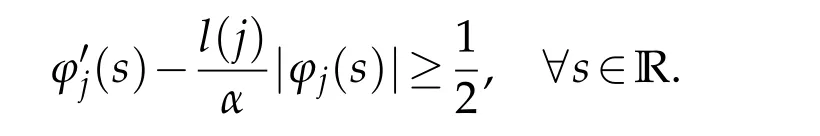
LetM=4j+h.SinceDiwn=0 on{|un|＞M}andφj(wn)has the same sign asunon the set{|un|＞j}(indeed,ifun ＞jthenun-Th(un)≥0 andTj(un)-Tj(u)≥0,it follows thatwn ≥0).Similarly,we show thatwn ≤0 on the set{un ＜-j}.

By takingφj(wn)as a test function in(3.1),we obtain

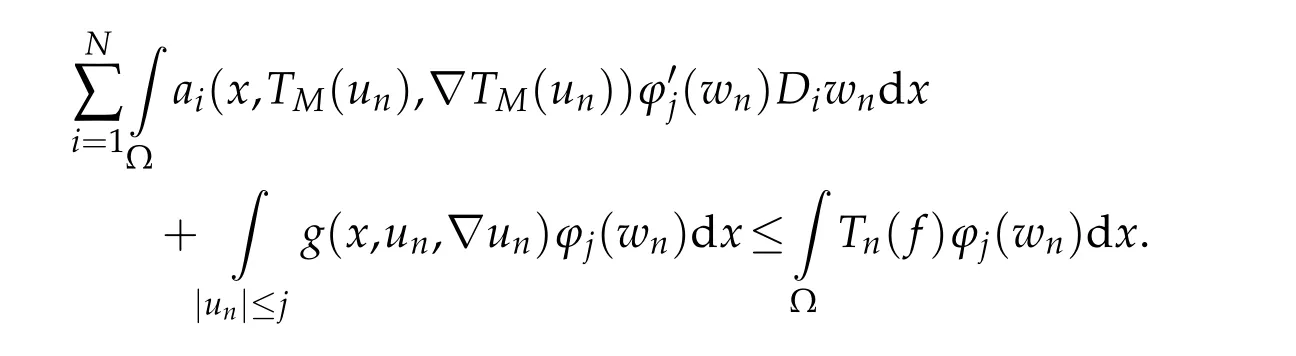
Takingyn=un-Th(un)+Tk(un)-Tk(u),we have

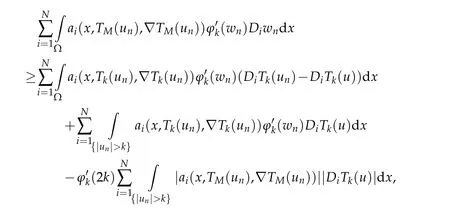
that is equivalent to

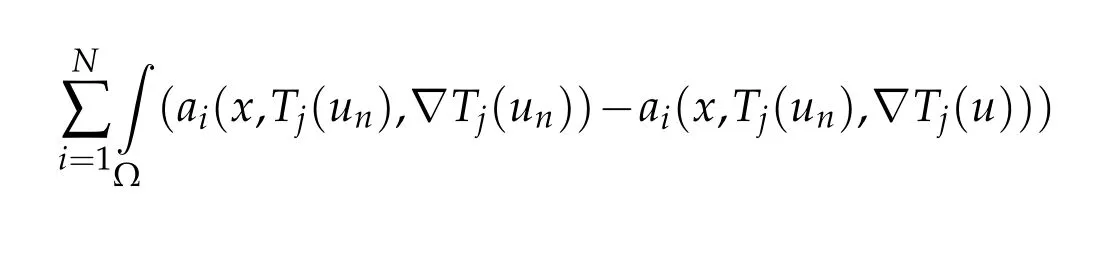
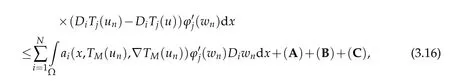
where

Arguing as in[13],we can prove that

By(3.16)and(3.17)we conclude that

Using(3.18)and arguing as in[13],we get

Thanks to(3.18)and(3.19),we obtain

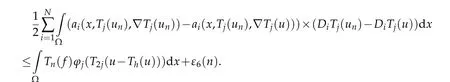
Then by lettinghtends to infinity in the previous inequality,we get

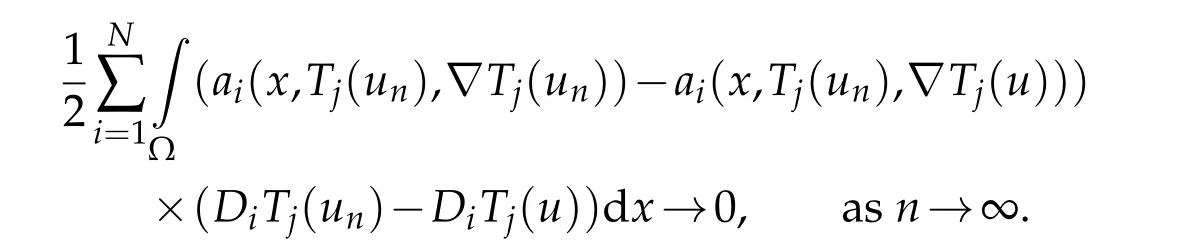
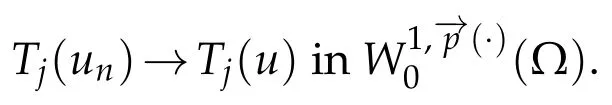
Thanks to Lemma 2.2,we obtain

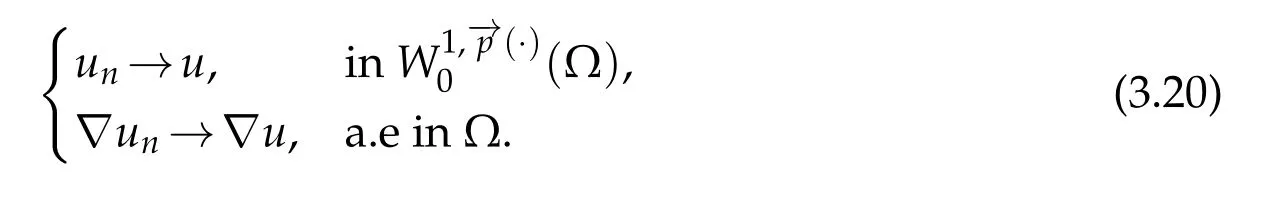
3.4 The equi-integrability of g(x,un,∇un)and passage to the limit

Thanks to(3.20),we have

Using that(ai(x,un,∇un))nis bounded in,and Lemma 2.1,we obtain

Now,letEbe a measurable subset of Ω.For allm＞0,we have by using(1.6)

Since(DiTm(un))nconverges strongly inthen for allε＞0,there existsδ＞0 such thatmeas(E)＜δand

On the other hand,usingT1(un-Tm-1(un))as a test function in(3.1)form＞1,we obtain

there existsm0＞0 such that

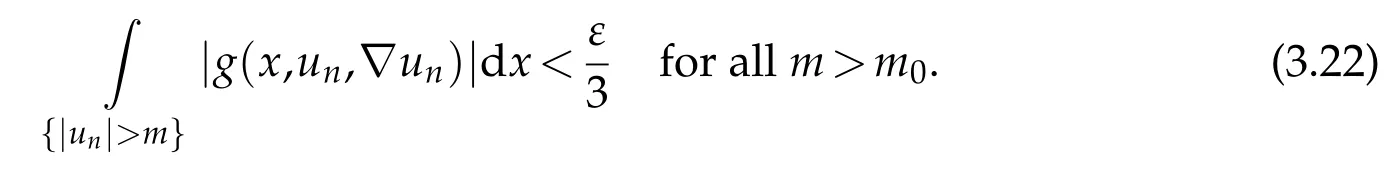
Using(3.21)and(3.22),we deduce the equi-integrability ofg(x,un,∇un).In view of Vitali’s theorem,we obtain

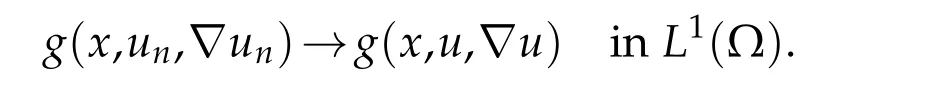
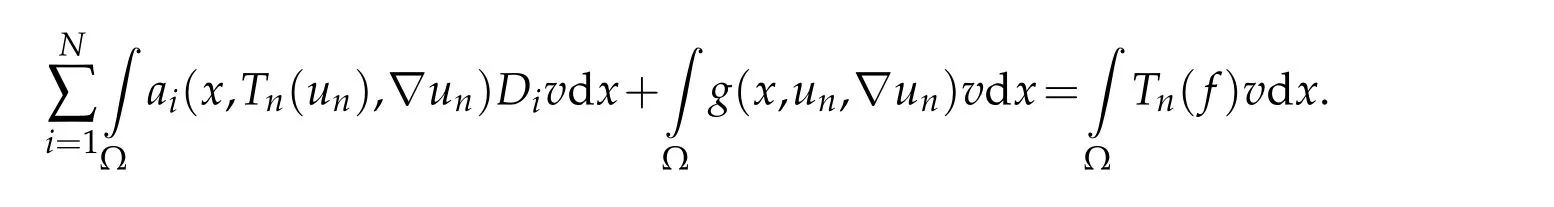
Lettingn →+∞,we can easily pass to the limit in this equation,to see that this last integral identity is true foruinstead ofun.This proves Theorem(2.2).

Example 3.1.As a prototype example,we consider the model problem

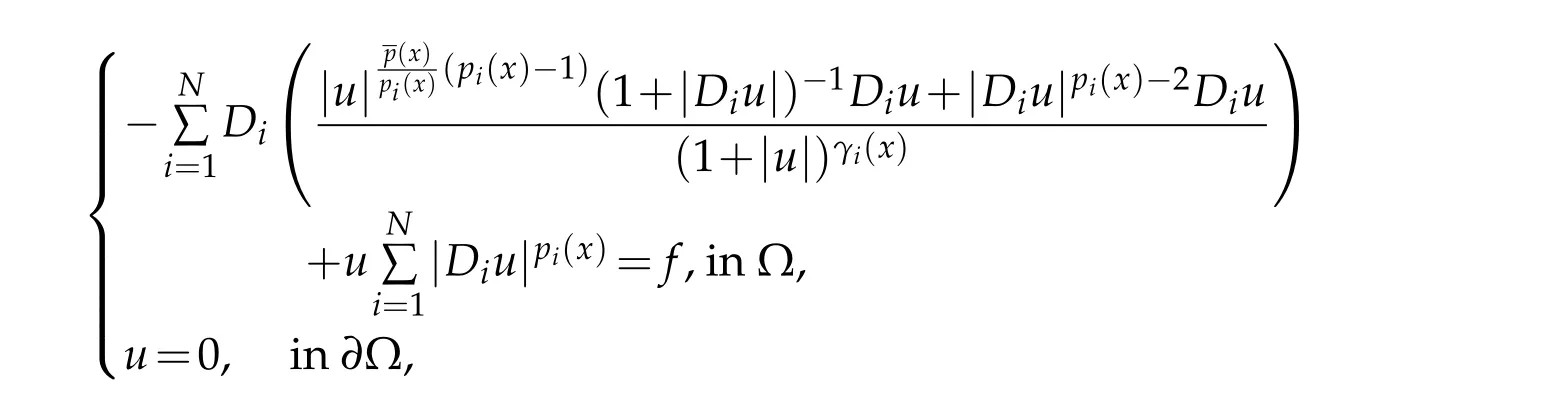
wheref ∈L1(Ω)andas in Theorem 2.2.

Acknowledgments

The authors would like to thank the referees for the useful comments and suggestions that substantially helped improving the quality of the paper.