Alloying and magnetic disordering effects on phase stability of Co2Y Ga(Y =Cr,V,and Ni)alloys:A first-principles study

Chun-Mei Li(李春梅), Shun-Jie Yang(杨顺杰), and Jin-Ping Zhou(周金萍)

College of Physics Science and Technology,Shenyang Normal University,Shenyang 110034,China

Keywords: first-principles, martensitic transformation, elastic modulus, magnetic ordering, shape memory alloys

1. Introduction

Several Co2-based Heusler alloys(with the stoichiometric composition X2YZ) such as Co—Ni—Ga,[1,2]Co2Cr(Ga,Si),[3]Co2Cr(Al,Si),[4]Co—V—Ga,[5—9]and Co—V—Si[10,11]recently have attracted a lot of research due to their extrordinary shape memory effect. This is because they possess the reversible martensitic transformation (MT) from theL21phase (facecentered-cubic,fcc,space groupFm¯3m)to the so-calledD022phase (body-centered-tetragonal, bct, space groupI4/mmm),described clearly in Ref.[12]although in some compositions,other related structures,such as the inverse Heusler(L21)[13,14]and the disorderedB2cubic phases,[2,15]and the orthorhombic and monoclinic martensite,[16]may also coexist. Among them, Co2Cr(Ga,Si) alloys can also occur withL21—D022—L21successive transitions upon cooling from the paramagnetic (PM) state to the ferromagnetic (FM) state,[3]showing an abnormal behavior of reentrant martensitic transformation(RMT) fromD022toL21. Some PM state of Co—V—Si alloys can even exhibit their shape memory effect up to about 700°C,[10]higher than the MT temperatures (TM) measured in most shape memory alloys. Compared to the traditional Ni—Mn—Ga alloys,these Co2-based shape memory alloys also possess relatively good mechanical property, processability,and corrosion resistance.[10,17]They therefore have a broad prospect for applications in the area of biomedicine, automotive,aerospace,and chemistry industry.

Similar to the traditional Ni—Mn—Ga alloys,the reversible MT behavior of these Co2-based shape memory alloys is highly composition-dependent. With respect to the composition,TMchanges from 250 K to 500 K in Co—V—Ga alloys,[5,6]and in Co—Ni—Ga alloys it even varies from 100 K up to 800 K.[18,19]The phenomenon of RMT fromD022toL21was clearly observed only in some Co2Cr(Ga,Si) alloys,[3,20]TMfor the normal MT ofL21—D022and that for the RMT change oppositely against the composition. Correspondingly,in these alloys the entropy difference between theL21andD022phases has been confirmed to be positive during the RMT but negative in the normal MT,[3,20]and during the two phase transitions, an inverse temperature dependence of superelastic stress[12,20]as well as electric resistivity[3]was also found in Co49.7Cr28.3Ga11Si11alloy. Exploring the alloying effect on the thermodynamic properties and phase stabilities of these Co2YGa(Y=Cr,V,and Ni)Heusler alloys and then trying to find out their physical mechanisms are critical to design them with good shape memory effect.However,until now,their true story is still not deeply understood.

There are several plausible quantities to connect the composition andTMof Ni—Mn—Ga alloys, such as the number of valence electrons per atom (e/a),[21—23]the energy difference between the cubic austenite and the tetragonal martensite(ΔEAM),[24]the tetragonal shear modulus of the parent phase(C′=(C11-C12)/2),[25,26]and the tetragonality of the martensite(|1-c/a|).[27,28]Generally,TMincreases with the increase ofe/a,ΔEAM,and|1-c/a|,whereas decreases with increasingC′. The established correlation betweenTMande/ais also followed by the most Co2YGa(Y=Cr,V,and Ni)-based alloys.[3,6,18,19]Nevertheless,the relationships ofTM～ΔEAM,TM～|1-c/a|,andTM～C′have never been examined.In addition,similar to Ni—Mn—In alloys,[29]the excessive Mn atoms on the In sites are FM coupling with those on their own sites in theL21phase, whereas in the tetragonalD022martensite they turn out to be anti-ferromagnetic (AFM) coupling with each other,in Co2Cr(Ga,Si)alloys the RMT occurs at the FM state whereas the normal MT happens at the PM state.[3,20]The magnetic ordering therefore may also be associated with the phase stability of these Co2-based alloys at finite temperatures. Furthermore, the MT fromL21to tetragonal pase in Ni—Mn—Ga can be traced to the Jahn—Teller distortion and Fermi surface nesting at the electronic structure level.[30,31]This electronic origination as well as the alloying and magnetic ordering effects on the MT also needs to be ascertained in these Co2-based shape memory alloys.

In this paper, we systematically investigate both the alloying and magnetic disordering effects on the thermodynamic properties and phase stabilities of theL21andD022phases of Co2YGa (Y=Cr, V, and Ni) Heusler alloys, and then try to find out the physical mechanisms driving their compositiondependent MT. In order to have a better comparison among the three groups of alloys,the other complicated structures are neglected in both the austenite and martensite. Though for the FMY=Ni alloy,the inverse Heusler structure[13]is also found to be lower than theL21structure in energy about 0.23 mRy from our calculations. However, the latter structure corresponds to the ground state of bothY=Cr and V alloys,and the MT ofL21—D022can be found in Co2NiGa alloy as well.[13]The rest of the paper is arranged as follows: In Section 2,we describe the first-principles method used and the calculation details. In Section 3, the site occupation, equilibrium properties, elastic property, and phase stability of nine groups of off-stoichiometric alloys as well as the three stoichiometric ones are presented at both the FM and PM states, the alloying and magnetic ordering effects on these properties are explored,and the mechanism driving the composition-dependent MT of these alloys is discussed together with their calculated electronic structure.Finally,we summarize the main results of this work in Section 4.

2. Methods and calculation details

Based on density-functional theory(DFT),the employed first-principles solver is the exact muffin-tin orbitals(EMTO)method,[32—35]in combination with the optimized overlapping muffin-tin approximation for the effective potential[32,36]and the full-charge density technique for the total energy.[35,37]This approach is then suitable to accurately describe the total energy change with respect to anisotropic lattice distortions.In addition,within the EMTO method,the single-electron Kohn—Shan equations are solved by using Green’s function technique and the substitutional disorder is treated using the coherent potential approximation (CPA).[38—40]Our main motivation for choosing this method is that it is flexible enough to describe both the atomic disorders and magnetic disorders in the Co2YGa (Y=Cr, V, and Ni)-based alloys. In a number of previous studies,[41—45]the accuracy of the EMTO-CPA method for the equation of state and elastic properties of metals and disordered alloys has been demonstrated.

For the present application,the EMTO basis sets include s, p, d, and f components, and the scalar-relativistic and softcore approximations are adopted. The Green function is calculated for 32 complex energy points distributed exponentially on a semicircular contour. As pointed out in Refs.[32,35,36],the EMTO results can be improved by optimizing the overlapping potential spheres. Here, after a careful potential optimization, we set the muffin-tin radii (RComt) and atomic radii(RCows)of the atoms on the Co sublattice beingRComt=0.95RwsandRCows= 1.10Rws, respectively, and keep those of atoms on the other sublattices equal toRws(Wigner—Seitz radius of the Voronoi polyhedron around each site). In the one-center expansion of the full-charge density, the number of components is truncated at 10. Thee/aratio is calculated with Co-3d74s2,Cr-3d54s1,V-3d34s2,Ni-3d84s2,and Ga-4s24p1. The electronic exchange-correlation potential is described with the generalized gradient approximation by Perdew, Burke, and Ernzerhof.[46]The Brillouin zone is sampled by a 17×17×17 uniformk-point mesh without smearing technique for both the cubic and tetragonal structures.

The equilibrium lattice parameters (aandc/a) and the bulk modulus(B)of both theL21andD022phases(described clearly in Ref. [12]) are first determined by fitting the calculated total energies (E) versus volume (nine data points) to a Morse function.[47]Here thec/aratio of the tetragonal structure is defined by means of the equivalent fct (face-centeredtetragonal) unit cell and then, whenc/a= 1 the tetragonal structure right means theL21structure. At the fixed equilibrium volumeV,the elastic constants of a single crystal can be derived by straining the lattice and then calculating the second derivative of the total energy ΔEto the strainδ. The lattice deformations and corresponding mathematical formula for the calculation of the elastic constants in both the cubic and tetragonal structures may be found in Ref. [48]. Throughout the present work, in order to get good fitting coefficients, six strains fromδ=0 to 0.05 with intervals of 0.01 are used to calculate the total energies. The corresponding polycrystalline elastic constants are estimated by means of the Hill average method.[32]

The temperature-dependent magnetism is evaluated with the performance of Uppsala Atomistic Spin Dynamics (UppASD)program.[49—53]Within this method,the itinerant electron system is mapped to an effective classical Heisenberg model,disordering degreeyis named as the magnetic disordering degree,which is connected with the temperature-dependent normalized magnetic moment (M/M0≈1-2y, withMandM0the magnetic moments at any temperatureTand 0 K,respectively).

In our calculations, the periodic box size is kept to 10×10×10 unit cells. The time-step for solving the above differential Eq. (2) is 10-16s, and the number of the time steps is taken as 10000. Theαis set 0.01. The 0 KJijincludes the exchange interactions between the atoms within the tenth nearest neighbors. They are calculated using the magnetic force theorem[54,55]implemented in the EMTO program.[35]The magnetic excitations gradually transform the FM magnetic moment into the PM (described by the disordered local magnetic-moment model,[56]DLM) magnetic moment over a temperature interval of Curie temperatureTC. During this process,with the partially disordered local magnetic-moment(PDLM) model,[57,58]the Co2YGa system may be described as a(Co↑2Y↑)1-y(Co↓2Y↓)yGa pseudoalloy. Here, the magnetic

whereBi=-∂H/∂miis the so-called effective field experienced by each atomi,γis the gyromagnetic ratio,andbi(t)is a stochastic magnetic field with a Gaussian distribution with respect to temperatureT. The magnitude ofbi(t)is related to the damping parameterα,which eventually brings the system into thermal equilibrium.With the solvedmifrom Eq.(2),the magnetic moment of the system(M)is then calculated from

3. Results and discussions

3.1. Equilibrium properties of the austenite

3.1.1. The standard stoichiometric alloys

Table 1 compares the equilibrium properties of theL21phase of Co2YGa(Y=Cr,V,and Ni)alloys with the available experimental and theoretical results.

It is clear that at the FM state, the presenta,B, total magnetic moment(μtot),and magnetic moments on Co(μCo),Y(μY), and Ga (μGa) atoms of the three alloys are in good agreement with their previous theoretical ones.[2,13,62,63,66—68]For Co2CrGa and Co2VGa alloys, theaandμtotvalues are also in line with their experimental data.[59—61,64,65]Since the atomic radii of Cr, V, and Ni are about 1.85 °A, 1.92 °A, and 1.62 °A,respectively,aof Co2VGa is the largest whereas that of Co2NiGa is the smallest. As is expected,aof the two alloys becomes smaller at the PM state(shown in the parentheses). However,in the PM Co2CrGa alloy,it becomes slightly larger,being consistent with our previous result.[44]It may be attributed that in the alloy, the Co, Cr, and Ga atoms are arranged much more closely together due to their stronger interactions at the ground FM state than the high temperature PM one.Bis shown in softening for all the three alloys with the PM ordering.

As listed in Table 1,μCoturns out to be different in the three FM cubic alloys, and among them theμYvalues also have big changes. As a result,μtotof Co2CrGa alloy is the largest whereas that of Co2VGa is the smallest. As shown in Fig. 1, the critical temperature, at whichM/M0gets close to 0 andχreaches the maximum, thus decreases withYvarying from Cr to Ni and then to V. Their estimatedTCvalues are about 474 K,422 K,and 347 K,respectively, also in line with the available experimental data[61,65]in Table 1. Above results ensure the accuracy of the present EMTO and UppASD calculations of these Co2-based Heusler alloys.

Table 1. Equilibrium lattice parameter (a), bulk modulus (B), total magnetic moment (μtot), magnetic moments on Co (μCo),Y (μY), and Ga (μGa)atoms,and Curie temperature(TC)of the FM L21-Co2YGa(Y =Cr,V,and Ni)alloys are in comparison with the experimental and theoretical data from Refs.[2,13,59—68]. For comparison,a and B of the three alloys with the PM ordering are also given in the parentheses.

Fig. 1. Temperature dependence of the normalized magnetic moment(M/M0, with M and M0 being the magnetic moment at any temperature T and 0 K,respectively)and magnetic susceptibility(χ)of the FM L21-Co2YGa(Y =Cr,V,and Ni)alloys.

3.1.2. The off-stoichiometric alloys

For the off-stoichiometric Co2YGa (Y=Cr, V, and Ni)alloys, we first determine their site preference by comparing the free energies (F) per atom of an alloy with different site occupations at their equilibrium volume. The lower theFis,the more stable the corresponding site configuration is. Here,Fis calculated by taking both the electronic total energyEand the chemical mixing entropy into account,expressed as

wherexiis the composition at each of the four sublattices,kBis the Boltzmann constant,andT=300 K.We consider the three types of compositions: Co-rich (Co2.1Y0.9Ga, Co2.1YGa0.9,and Co2.1Y0.95Ga0.95),Y-rich(Co1.9Y1.1Ga,Co2Y1.1Ga0.9,and Co1.95Y1.1Ga0.95), and Ga-rich (Co1.9YGa1.1, Co2Y0.9Ga1.1,and Co1.95Y0.95Ga1.1) alloys. For each composition, the normal occupancy (the excessive atom evenly occupying all the sites of the deficient atoms)and the abnormal occupancy(the excessive atom occupying solely the site of one of the other two atoms,and then the replaced atoms moving to the sublattice of the left deficient atom)are considered.

In Table 2, the relative electronic total energy (ΔEand ΔE′, for the spin-polarized and nonspin-polarized compositions, respectively, with the same spin-polarized equilibrium lattice constants)as well as free energy(ΔF)of each alloy to that of the alloy with the normal site configuration is shown.For each alloy, the difference between ΔEand ΔFwith the same site-occupation configuration is very small at 300 K.Then, around the room temperature, the mixing entropy cannot change the relative stability of the site occupations such that comparing the electronic energy is actually sufficient to determine the stable site occupancy.

For the Co-rich alloys withY=V and Ni, they always possess the lowest ΔEwhen the excessive Co atom is in the normal site, i.e., evenly occupies the sites of the deficient atoms, whereas these alloys withY=Cr are the most stablewhen the excessive Co atom occupies the Cr sublattice no matter whether Cr is deficient or not. TheY-rich alloys withY=Cr and V possess the smallest ΔEwhen the excessiveYatom takes the normal site as well, whereas when it occupies the Co sublattice these alloys withY=Ni turn out to be the most stable. The Ga-rich alloys always have the lowest energy when the excessive Ga atom occupies theYsublattice no matter whetherYis deficient or not. Therefore, it is concluded that in these off-stoichiometric alloys, the excessive Co atom favors theYsublattice in theY=Cr alloys,and the excessiveYatom prefers the Co site in theY=Ni alloys, whereas the excessive Ga atom always tends to take theYsublattice.

Table 2. Relative electronic total energy (ΔE and ΔE′, calculated with and without spin-polarization, in mRy) and free energy (ΔF, in mRy) of the off-stoichiometric L21-Co2YGa (Y =Cr, V, and Ni) alloys to those of these alloys with normal site occupancy configuration, at temperature of 300 K.ΔE and ΔE′ are evaluated with the same spin-polarized equilibrium lattice constants. Also presented in the table are the total magnetic moments(μtot,in μB)of these FM alloys with different configurations.

Listed in Table 2 are alsoμtotvalues of these offstoichiometric alloys with different site occupations. Examining the local magnetic moments on each sublattices (not shown in the table), we find that bothμCoandμYchange when Co andYare on the different sublattices. Here,μYcorresponding to theYatom on the Co sublattice is even antiferromagnetic coupling with that to theYatom on its own site whenY=Cr and V.Therefore,μtotof each alloy changes with different site-occupation configurations. Obviously, the site occupancy of these off-stoichiometric Co2YGa alloys is controlled by the complex interaction between the chemical and magnetic effects. In Table 2, it is seen that ΔEgenerally differs dramatically from ΔE′,indicating that the magnetic effect on the site occupancy should be very strong. In some groups ofY- and Co-rich alloys, the magnetic effect even alters the stability sequence of the site occupations. Calculated without polarization, instead of being the normal site, the excessive Co atom changes to take the Ga sublattice in theY=V alloys,and the excessiveYatom changes to occupy the Co site in theY=Cr alloys. In these off-stoichiometric alloys,the magnetic effect seems to stabilize the normal site-occupation configuration. Contrarily, in theY=Cr alloys the excessive Co atom is nevertheless found going back to the normal site from nonspin-polarized calculations.The magnetic effect is complicated and composition dependent.It is noted thtatμGais much small and almost negligible.Calculated with and without spinpolarization,the determined stable site-occupation configurations are the same in each Ga-rich alloy.

With the determined stable site-occupation configuration, we calculate the equilibrium properties of the nine groups of off-stoichiometric alloys: Co2Y(Ga1-xCox) and Co2Y(Ga1-xYx)(Y=Cr,V,and Ni),Co2(Y1-xCox)Ga(Y=Cr and V), and (Co1-0.5xNi0.5x)2NiGa (Co2(Ni1+xCo-x)Ga) alloys (x= 0.05, 0.10, 0.15, and 0.20), since in these alloys with increasingxthee/aratio increases and the MT is then hoped to be promoted. As shown in Table 3, it is found thataof Co2Y(Ga1-xCox) alloys always decreases with increasingxdue to the atomic radius of Co (1.67 °A) being much smaller than that of Ga (1.81 °A). Following Vegard’law[69]as well,aof Co2(Cr1-xCox)Ga, Co2(V1-xCox)Ga,and Co2Ni(Ga1-xNix) alloys decreases with the increase ofxwhereas that of Co2V(Ga1-xVx) increases withx. Both Co2Cr(Ga1-xCrx) and (Co1-0.5xNi0.5x)2NiGa alloys are exceptions, where withxincreasing from 0 to 0.2,achanges no more than 0.0025 °A,since the atomic radii of Cr(1.85 °A)and Co (1.67 °A) are similar to those of Ga (1.81 °A) and Ni(1.62 °A),respectively. The calculated trends ofB～xare contrary to those ofa～xin most groups of these alloys except for Co2Cr(Ga1-xCox), Co2(Cr1-xCox)Ga, and Co2V(Ga1-xVx),where the trends ofB～xanda～xtend to be the same.In (Co1-0.5xNi0.5x)2NiGa alloys, due toμNi(～0.15μB) being much smaller thanμCo(～1.07μB),μtotdecreases with the Ni addition. In all the other alloys, nevertheless,μtotalways increases withxbecause there the local magnetic moment of the doped atom is always larger than that of the replaced atom.Even in Co2(Cr1-xCox)Ga alloys, on the same Cr sublatticeμCo(～1.75μB) is also larger thanμCr(～1.50μB), although the latter(～1.57μB)is almost twice the former(～0.75μB)in the FML21-Co2CrGa alloy.

Table 3. Equilibrium lattice parameter(a,in °A),bulk modulus(B,in GPa),and total magnetic moment(μtot,in μB)of nine groups of off-stoichiometric Co2YGa(Y =Cr,V,and Ni)alloys with the FM L21 phase: Co2Y(Ga1-xCox)and Co2Y(Ga1-xYx)(Y =Cr,V,and Ni),and Co2(Y1-±xCo±x)Ga(+for Y =Cr and V and—for Y =Ni). Four compositions of x=0.05,0.10,0.15,and 0.20 are calculated for each group of alloys.

3.2. Martensitic transformation

3.2.1. The stoichiometric alloys with the FM ordering

Figure 2 shows the electronic total energiesEof the FM Co2YGa (Y=Cr, V and Ni) alloys as a function ofc/aandrws. At the ground FM state,Eof the three stoichiometric alloys shows two minima: one is atc/a= 1, meaning theL21parent phase, and another one is aroundc/a=1.25 forY=Cr, V and nearc/a=1.40 forY=Ni, corresponding to the tetragonalD022phase. In comparison, for both Co2CrGa and Co2VGa alloys,theL21phase is lower than the tetragonal one in energy,meaning that the two stoichiometric alloys can not occur with the MT even at 0 K.Then,the FM cubic phase corresponds to their ground state. For Co2NiGa alloy, nevertheless, the energy of the obtainedD022structure is lower than that of theL21structure. At low temperatures,it can occur with the MT and possess theD022martensite. The estimated equilibriumV,c/a,B,andμtotvalues of the martensitic Co2NiGa alloy at the FM state are about 11.594 °A3, 1.3835,181.1 GPa, and 2.85μB, respectively,in good agreement with the previous theoretical results(11.57 °A3,1.41,180 GPa,and 2.92μB,respectively).[13]

Fig.2. Electronic total energy(E,in Ry)contours of the FM Co2YGa(Y =Cr, V, and Ni) alloys as a function of the tetragonal lattice ratio(c/a)and the Wigner—Seitz radius(rws).

3.2.2. Magnetic disordering effect

In order to investigate the magnetic ordering effect on the MT of Co2YGa(Y=Cr,V and Ni)alloys,with the fixed equilibriumVat the FML21phase,we calculate their relative electronic total energies ΔEto theL21phase change with respect toc/aat the different magnetic disordering degreeyvalues.Their obtained trends of ΔE～c/achange againstyare shown in Fig. 3. In eachy, we can find two energy minima as well in all the three alloys. The one atc/a=1 means the cubicL21phase,whereas another one abovec/a=1 corresponds to the tetragonalD022phase. In Co2NiGa alloy,with a negative value ΔEof the tetragonal phase(c/a～1.30—1.40)decreases with increasingy, indicating that the magnetic disordering further promotes the occurrence of the MT. In Co2CrGa and Co2VGa alloys,ΔEof the obtainedD022phase(c/a～1.20—1.30)also becomes lower and lower with the increase ofy,and wheny=0.2 it changes from positive to negative. The critical value ofy=0.2 meansM/M0=0.6. As seen from Fig. 1,in the two alloys it corresponds toT=390 K and 250 K,respectively. There, before transiting to the PM state, the two stoichiometric alloys thus have already been able to occur with the MT and possess the tetragonalD022phase.Therefore,contrary to the traditional Ni—Mn—Ga alloys,[70]where during the heating process at low temperatures, the cubic parent phase gets relatively more and more stable,in Co2CrGa and Co2VGa alloys the tetragonalD022martensite gradually changes to be stabilized instead with increasingTdue to the magnetic excitations. The magnetic and structural transitions tend to couple each other there,meaning that the metamagnetic MT[5]is also confirmed in the two stoichiometric compositions.

Fig. 3. Relative electronic total energy (ΔE) of Co2YGa (Y =Cr, V and Ni) alloys to that of their L21 structure change with respect to the tetragonal lattice distortion (c/a), calculated at the different magnetic disordering degree(y,0 ≤y ≤0.5).

From Fig. 3, it is also noted that withyincreasing from 0 to 0.5, ΔEof the tetragonal martensite decreases about 3.6 mRy and 2.5 mRy in Co2CrGa and Co2VGa alloys,respectively,but merely less than 0.5 mRy in Co2NiGa alloy. In fact,with the increase ofy,μtotof both theL21andD022phases decreases whereas theirEvalues increase. It is thus obvious that in eachy ＞0, the increase of the energy of the parent phase is higher than that of the tetragonal martensite in the three alloys,and in comparison,the magnetic disordering effect on the relative stability of theD022martensite is more dominant in Co2CrGa and Co2VGa alloys. This result could be attributed to thec/a-dependentμtotof the three FM(i.e.,y=0)alloys.Described in Fig.4,in the FM Co2NiGa alloy,theμtotvalues corresponding toc/a=1 and 1.40(2.6μBand 2.8μB,respectively)are almost comparable and in the alloy, the energy increases of the austenite and martensite in eachy ＞0 are then induced by a similar decrease of theirμtot.However,in the FM Co2CrGa and Co2VGa alloys,μtotof theL21phase is much larger than that of the tetragonal phase (c/a ≈1.20—1.25),about 1.5μB—1.6μB. There, in each ofy ＞0 the decrease ofμtotis therefore relatively much more in the austenite. It consequently further accelerates the energy increase of the phase relative to the tetragonal martensite in the two magnetic disordered alloys. In Co2VGa alloy,μtotpossesses a large value in Fig.4 only whenc/a=1 and 1.05,about 1.82μBand 1.48μB,respectively. For the otherc/avalues, the Co and V atoms change to be almost non-spin-polarized as well as the Ga atom,and thereμtotis then close to 0. It indicates that the MT ofL21—D022and the magnetic transition in the alloy may couple each other.

Fig.4. Total magnetic moments(μtot)per unit cell of the FM Co2YGa(Y =Cr,V and Ni)alloys versus the tetragonal lattice distortion(c/a).

At the PM state, Co2YGa (Y=Cr, V and Ni) alloys are all stabilized by theD022martensite. The estimatedV,c/a,andBvalues are about 11.686 °A3,1.2307,and 194.1 GPa for Co2CrGa,11.864 °A3,1.2228,and 206.6 GPa for Co2VGa,and 11.526 °A3,1.3509,and 175.6 GPa for Co2NiGa,respectively.In comparison with theL21parent phase, bothμCoandμYof the tetragonalD022phase in their absolute values greatly decrease in the former two alloys but slightly increase in the last one as well as those of the three FM alloys. As a result,due to the magnetovolume effect:[71]the increase of the local magnetic moment of a system generally corresponding to the expansion of its volume,upon the MT theVvalues of the three PM alloys change about-1.0%,-1.1%, and 0.2%, respectively, whereas theirBvalues vary about 9.2%, 12.3%,and-1.8%, respectively. For the martensitic Co2NiGa alloy with the PM ordering,Vandc/aare slightly smaller whereasBbecomes larger than the corresponding FM alloy.

3.2.3. Alloying effect

We further investigate the alloying effect on the MT in the off-stoichiometric Co2YGa (Y= Cr, V and Ni) alloys. Since as well as Ni—Mn—Ga,TMof the most Co2-based shape memory alloys was also found to increase withe/a,[3,6,18,19]the nine groups of alloys with highere/aratio than their stoichiometric compositions shown in Table 3 are considered here. In Fig. 5, their curves of ΔE～c/achanging with respect toxare shown with the energy of the FML21structure (c/a= 1) taken as reference at both the FM and PM states. It is found that in each group of Ga-non-deficient Co2(Cr1-xCox)Ga, Co2(V1-xCox)Ga, and(Co1-0.5xNi0.5x)2NiGa alloys (Figs. 5(c), 5(f), and 5(i)), the curve of ΔE～c/achanges very small withxincreasing from 0 to 0.2 at the two magnetic states. The alloying effect on their MT then seems to be negligible in the studied composition range. In the FM state of Co2Y(Ga1-xCox) and Co2Y(Ga1-xYx) alloys withY=V (Figs. 5(d) and 5(e)) and Ni(Figs.5(g)and 5(h)),with increasingx,ΔEof the obtained tetragonal structure abovec/a=1 becomes lower and lower.Its value aroundc/a=1.25 then changes from positive to negative in the two groups ofY=V alloys whenxincreases up to 0.2 and 0.4,respectively. As well as all the FMY=Ni alloys, these FM Co2V(Ga1-xCox) and Co2V(Ga1-xVx) alloys withx ≥0.2 andx ≥0.4,respectively,then also have the MT behavior at 0 K.With increasingx,thec/aratio of theirD022structure tends to slightly increase withx(i.e.,e/a).

In the FM Ga-deficient alloys withY= Cr (Figs. 5(a)and 5(b)),the obtained tetragonal structure aroundc/a=1.25 tends to possess a higher and higher ΔEvalue with increasingx. This means that,in these alloys,increasing thee/aratio by replacing the Ga atoms with Co and Cr atoms favors theL21parent phase getting more and more stable instead, and then further suppresses the MT. However, it promotes the RMT fromD022toL21there at low temperatures. Correspondingly,TMfor their RMT then tends to decrease with increasingx(e/a)since the energy barrier between the two phases becomes lager and larger with Co and Cr doping. The established contrary trends ofTM～xfor the MT at the PM state and the RMT at the FM state are in good agreement with those measured in the Co2Cr(GaSi)shape memory alloys.[3]

Fig.5. Relative electronic total energies(ΔE)of the FM and PM Co2Y(Ga1-xCox)and Co2Y(Ga1-xYx)(Y =Cr,V,and Ni),Co2(Y1-xCox)Ga(Y =Cr and V),and(Co1-0.5xNi0.5x)2NiGa alloys versus the tetragonal lattice distortion(c/a). Here,the electronic energy of the FM L21 structure(c/a=1)is taken as reference for each alloy. The range of concentration x is 0 ≤x ≤0.4 for Co2V(Ga1-xVx)and 0 ≤x ≤0.2 for the other groups of alloys.

At the PM state, ΔEof each alloy corresponding to theD022structure is always lower than that to theL21one in Fig. 5, and then all these PM off-stoichiometric alloys can occur with the MT as well. In the Ga-deficient Co2Y(Ga1-xCox) and Co2Y(Ga1-xYx) alloys, with increasingx(i.e.,e/a),thec/aratio of the tetragonal martensite slightly increases, whereas ΔEcorresponding to the structure gradually becomes lower and lower than that to theL21structure.Then,theD022phase becomes more and more stable than theL21phase with Co andYdoping. This indicates that in these PM alloys,the MT is promoted with the increase ofe/a,corresponding to the increase of theirTMwithe/a.It is also noted that in all theseY=Cr and V alloys,ΔEof theD022structure corresponding to the PM state is always not much higher than that to the FM one, and in some compositions they are even similar. It indicates the low magnetization and magnetic excitation energy of their tetragonal phase. The MT ofL21—D022therefore should tend to couple with the magnetic or metamagnetic transition in theseY=Cr and V alloys.

3.3. Elastic properties

3.3.1. The standard stoichiometric alloys

Table 4 lists the calculated static elastic constants of the stoichiometric Co2YGa (Y= Cr, V and Ni) alloys with the austenitic and martensitic phases,in comparison with the previous theoretical results.[2,45,72]It is shown that in the FML21phase of the three alloys, the presentC11is slightly smaller butC12becomes slightly larger than our previous results calculated with the normal settings ofRmtandRws(i.e.,RmtandRwson all the sublattices are equal toRws).[45]As a result,their estimatedC′values as well asC44are smaller than those corresponding to the previous EMTO calculations.[45]However,it is clear that with the optimizedRComtandRCows(RComt=0.95RwsandRCows=1.10Rws), the evaluated shear elastic constantC′andC44are closer to those resulted from the first-principles full potential calculations shown in Table 4,[2,72]confirming again the accuracy of our present EMTO calculations.

The magnetic excitations gradually transform the system from the FM state to the PM one. Correspondingly, the elastic constants of Co2YGa (Y=Cr, V, and Ni) alloys can be assumed to change against the magnetic disordering degreeyincreasing from 0 to 0.5. Here, with the equilibrium volume at the FM state(y=0),C′,C44and the elastic anisotropy(A)of the threeL21alloys are then especially calculated at the differentyvalues. As shown in Fig.6,with increasingy,bothC′andC44of theY=Cr and V alloys decrease whereas for theY=Ni alloy,C′decreases andC44increases withy. The evaluatedAvalues of the three alloys all gradually increase with the increase ofy. This result indicates that in the three alloys,the magnetic disordering tends to soften the tetragonal shear elastic constantC′and then increase their elastic anisotropyA. Described in Table 4, when the FM state transiting to the PM one,C′decreases to 62.1% andAincreases to 1.6 times for Co2NiGa, for Co2CrGaC′decreases to 7.7% andAincreases to 10.7 times,and for Co2VGaC′even becomes negative. Thus,the magnetic disordering decreases the mechanical stability of theL21parent phase, which nevertheless favors the tetragonal lattice deformations and then promotes the MT in the three stoichiometric alloys.

Table 4. Single crystal elastic constants (in GPa), tetragonal shear elastic constant (C′ =(C11-C12)/2 and Cs =C11+C12+2C33-4C13, for the cubic and tetragonal structures, respectively, in GPa), shear modulus (G, in GPa), Young modulus (E, in GPa), Debye temperature (Θ, in K), elastic anisotropy(A),and the ratio of the shear and bulk modulus(G/B)of the FM and PM Co2YGa(Y =Cr,V,and Ni)alloys with the L21 and D022 phases,in comparison with those of theoretical ones taken from Refs.[2,45,72].

The stability criteria for tetragonal crystals areC11＞|C12|,C33＞0,C44＞0,C66＞0,C11+C33-2C13＞0, andCs(=C11+C12+2C33-4C13)＞0. From our calculations shown in Table 4, the elastic constants of the tetragonal alloys all satisfy the above conditions. It indicates that at 0 K,the tetragonal martensite is energetically and mechanically stabilized in the PM Co2CrGa and Co2VGa alloys, as well as in both the FM and PM Co2NiGa alloys. For the FMD022-Co2NiGa alloy,the present elastic constants seem to be comparable with those theoretical ones of the FML10-CoNiGa alloy.[16]

The plastic property of a material has been related to the ratio of the shear and bulk modulus (G/B). A high value ofG/B(greater than～0.57)generally means the inherent crystalline brittleness(ICB)of a bulk material. From Table 4,we find that theG/Bvalues of these stoichiometric alloys are all below this critical value and hence their ICB is low. In comparison with the FM ordering, the PM ordering also tends to decrease theG/Bratio of these cubic alloys.However,the MT seems to increase the ICB of these alloys. In both the FM and PM Co2NiGa and PM Co2CrGa alloys, theG/Bratio of the martensite is always larger than that of the austenite.

3.3.2. The off-stoichiometric alloys

Figure 7 showsC′,C44, andAvalues of the FM and PML21phase of the studied nine groups of off-stoichiometric Co2YGa(Y=Cr,V and Ni)alloys change with respect to the compositionx. For all the Ga-deficient Co2Y(Ga1-xCox)and Co2Y(Ga1-xYx)alloys,bothC′andC44decrease with increasingx(i.e.,e/a)at the PM state,whereas theirAvalues of theseY=V(Figs.7(d),7(e),and 7(f))and Ni(Figs.7(g),7(h),and 7(i)) alloys increase withx. For theY=Cr (Figs. 7(a), 7(b),and 7(c))alloys with the PM ordering,Ahas not been shown in Fig.7(c)since theirC′values are negative.Thex-dependentC′as well asAof these PM Ga-deficient alloys indicates that theirL21parent phase gets mechanically more and more unstable with the increase ofe/aratio,which nevertheless favors the tetragonal lattice deformations. At the FM state, bothC′andC44decrease with the increase ofxin these Ga-deficientY=V alloys whereas in the correspondingY=Ni alloys,C′decreases butC44increases withx. As a result,Aof all theseY=V and Ni alloys increases withxas well. Similar to their corresponding PM alloys, with the increase ofe/aratio,C′softens whereasAenhances, promoting the MT fromL21toD022. Correspondingly,as shown in Fig.5,with increasingxthe tetragonal phase of all these PM Ga-deficient alloys and the FM ones withoutY=Cr gets relatively lower and lower in energy in comparison with theL21parent phase.

For the FML21phase of Co2Cr(Ga1-xCox) and Co2Cr(Ga1-xCrx) alloys, with increasingxbothC′andC44increase whereasAdecreases. In these alloys, theL21parent phase gets mechanically more and more stable instead with the increase ofe/aratio, contrary to their correspondingY=V and Ni alloys. Correspondingly, as shown in Figs. 5(a) and 5(b), respectively, upon tetragonal lattice distortions, the cubicL21phase of the two groups of Ga-deficientY=Cr alloys becomes lower and lower in energy with increasingxin comparison with the obtained tetragonal phase,promoting the RMT fromD022toL21.

Fig.7. Shear elastic constants(C′ and C44)and elastic anisotropy(A)of the FM and PM L21 phase of Co2Y(Ga1-xCox)and Co2Y(Ga1-xYx)(Y =Cr,V and Ni),Co2(Y1-xCox)Ga(Y =Cr and V),and(Co1-0.5xNi0.5x)2NiGa alloys versus the composition x(0 ≤x ≤0.2).

For both the FM and PML21phases of Co2(Y1-xCox)Ga(Y=Cr and V) and (Co1-0.5xNi0.5x)2NiGa alloys, the evaluated trends ofC′～x,C44～x, andA～xare in line with those of their corresponding Ga-deficient alloys. In comparison, nevertheless, withxincreasing from 0 to 0.2, the variations ofC′andAare relatively smaller in each group of these Ga-non-deficient alloys. Then, the alloying effect on their elastic stabilities should be not as significant as it on those of the corresponding Ga-deficient alloys. Similarly, their curves of ΔE～c/aat both the magnetic states also have not a big change withxincreasing from 0 to 0.2 in Figs.5(c),5(f),and 5(i).Therefore,in these studied Ga-deficient Co2Y(Ga1-xCox)and Co2Y(Ga1-xYx)alloys,the composition dependence of the MT is closely related with their composition-dependentC′andAvalues: the increase of thee/aratio generally corresponds to the decrease ofC′but the increase ofA,which promotes the occurrence of the MT but suppresses the RMT behavior.

3.4. Electronic structure

To understand the atomistic origin of the phase stability of these studied Co2YGa-based Heusler alloys, we compare the total density of states (DOS)of their stoichiometric compositions with both the FM and PML21andD022phases. As shown in Figs.8(a)and 8(e),respectively,in the FML21phase of Co2CrGa and Co2VGa alloys,around the Fermi level there is a big peak in the majority (spin-up) DOS, while there is a deep band gap in the minority (spin-down) DOS, indicating that the two alloys exhibit a nearly half-metallic behavior in the FM cubic phase. As seen from the local DOS of Co (Figs. 8(b) and (f)), Cr and V (Figs. 8(c) and 8(g)), and Ga(Figs.8(d)and 8(h))atoms, it is clear that the big peak is contributed mainly by the degenerated Co d and Cr d (V d)electronic states,whereas the deep band gap originates mainly from the overlapping of the orbits between Co d and Ga p as well as Cr d(V d)and Ga p,i.e.,the strong covalent hybridization between them around the Fermi level.

Upon tetragonal distortions,the degenerated Co d and Cr d(V d)states dominating the big peak around the Fermi level split and there, these states may shift to lower or higher energy levels. Then,in the FMD022phase the big peak becomes smaller in Co2CrGa and it even disappears in Co2VGa. The redistribution of the majority DOS has nevertheless no great influence on the stability of the system.However,in the minority DOS, the deep band gap around the Fermi level becomes shallower in the two FM tetragonal alloys,since there the Co d and Cr d (V d) states increase upon tetragonal distortions.It indicates that in the FMD022phase, the covalent banding between Co and Ga as well as Cr(V)and Ga weakens,and the stability of the system then beomces worse. The calculated tetragonal shear elastic constantC′of the FML21phase of the two alloys are thus with very large values. With Co and Cr(V) substituting for Ga, this electronic structure mechanism should beomce more and more dominant, further suppressing the tetragonal lattice deformations. In the Ga-deficient Co2Cr(Ga1-xCox) and Co2Cr(Ga1-xCrx) alloys with the FM ordering(Figs.5(a)and 5(b),respectively),the calculated relative electronic energy ΔEof the tetragonalD022phase is thus higher and higher with increasingx, whereasC′of theL21phase increases butAdecreases withx(Figs.7(a)and 7(c),respectively). In all theseY=Cr alloys,the FML21phase is the ground state.

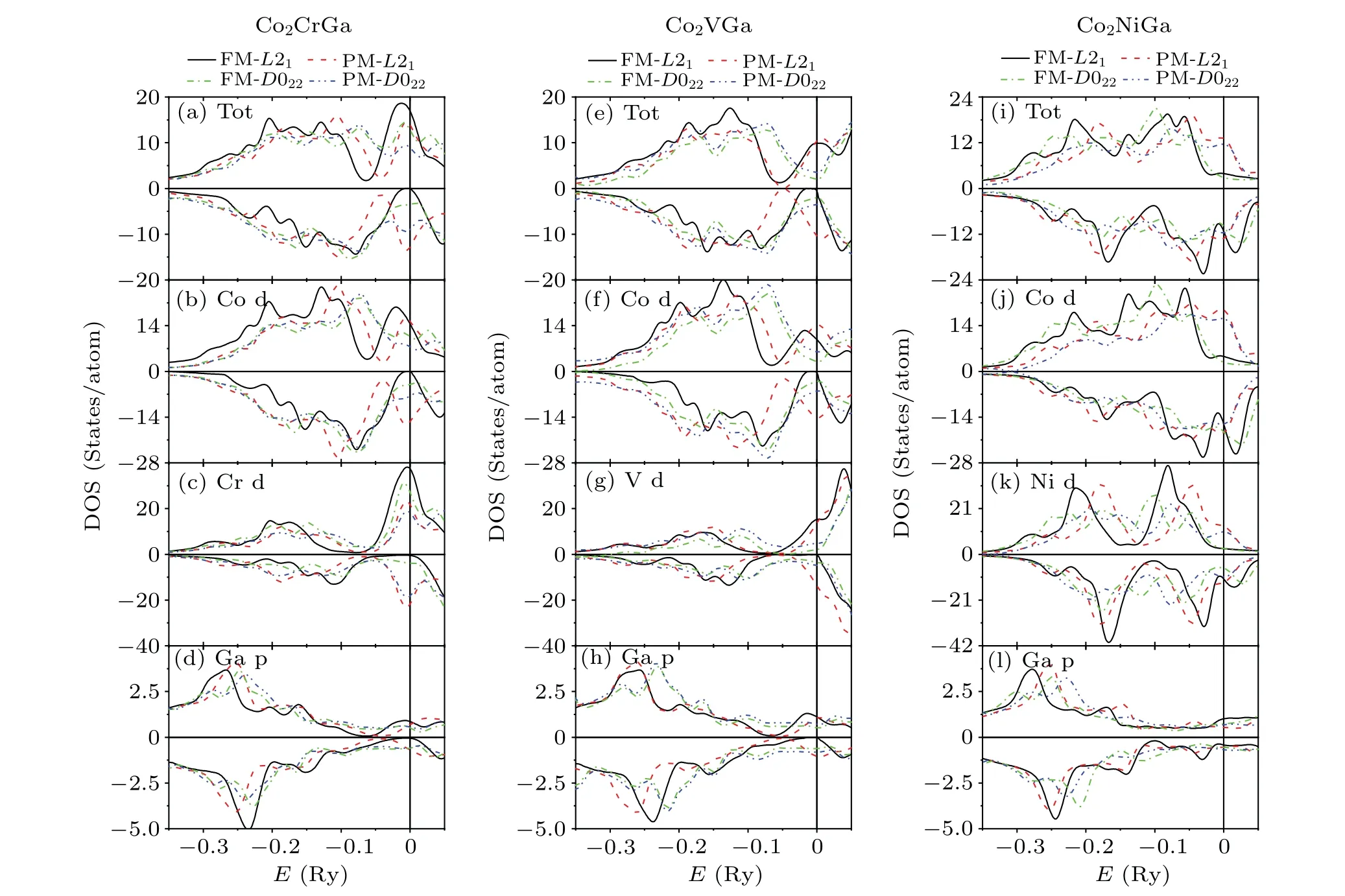
Fig.8. Total electronic density of states(DOS)[(a),(e),and(i)]and local DOS corresponding to Co[(b),(f),and(j)],Y [(c),(g),and(k)],and Ga[(d),(h),and(l)]of Co2YGa(Y =Cr,V and Ni)alloys with both the FM and PM L21 and D022 phases. The vertical lines indicate the Fermi level.

Unlike Co2CrGa alloy where the valley of the band gap is almost right at the Fermi level, in the FML21phase of Co2VGa alloy, the right sides of the band gap for Co d and Vd and then that for the total DOS are very close to the Fermi level.Consequently,upon tetragonal distortions,there some of the Co d and V d states (dominated by the former) shift near below the Fermi level. Then, the band gap in the total DOS of the alloy becomes shallower but wider at the same time in the FMD022phase. Replacing Ga with Co and V in Co2VGa alloy,the widening of the band gap should also become more and more significant as well as its getting shallow upon tetragonal distortions. However, contrary to the latter, the former indicates the covalent banding between Co and Ga as well as Cr and Ga getting stronger and stronger, and then ΔEof theD022phase becomes lower and lower with Co and V doping.It favorsC′of theL21phase decreasing butAincreasing withxin Co2V(Ga1-xCox)and Co2V(Ga1-xVx)alloys. Obviously,since in comparison with the correspondingY= Cr alloys,the contrary trends of ΔE～x(Figs. 5(d) and 5(e)),C′～x(Fig. 7(d)), andA～x(Fig. 7(f)) are estimated in these FMY=V alloys,upon tetragonal distortions the widening of the band gap is confirmed to have more and more dominant role on the phase stability than its getting shallow with Co and V doping in these alloys. Moreover, in comparison, the Co-doping should more favor this electronic structure mechanism, since upon tetragonal distortions the DOS change of Co d seems to be slightly larger than that of V d around the band gap in Co2VGa alloy. In eachx,C′is therefore relatively lower in the Co-doped alloys in Fig. 7(d) and shown in Fig. 5(d), whenxgoes up to 0.2,Co2V(Ga1-xCox)alloys turn out to possess the MT behavior,whereas Co2V(Ga1-xVx)alloys can occur with the MT untilx ≥0.4 in Fig. 5(e). Only in the two groups of Ga-deficientY=V alloys withx ＜0.2 andx ＜0.4, respectively,the FML21phase corresponds the ground state.

As shown in Fig. 8(i), in the FML21-Co2NiGa alloy,there are both majority and minority DOS located around the Fermi level,showing the metallic property of the alloy. Moreover, around the Fermi level in the minority DOS of the alloy, there is a pseudogap contributed by the overlapping of the orbits between Co d and Ga p as well as Ni d and Ga p.Upon tetragonal distortions, the pseudogap corresponding to Ni d becomes deeper and wider, and that for Co d becomes slightly shallower but wider. As a result, the pseudogap in the total DOS becomes wider in the FMD022phase, indicating the stronger covalent banding between Co and Ga as well as Ni and Ga, and then the more stability of the system.Thus,in Co2NiGa alloy the FM tetragonal phase corresponds to the ground state. This phase should further become relatively more and more stable with Co and Ni substituting for Ga and in comparison, the Ni-doping has a greater influence on its relative stability. Similarly, in eachx, the evaluatedC′value of the Ni-doped alloys (Fig. 5(g)) is also smaller than that of the Co-doped alloys(Fig.5(h)).

At the PM state,there is a big peak just right at the Fermi level in theL21phase of all the three stoichiometric alloys,dominated by the Co d andYd states. Similar to Ni—Mn—Ga alloys, this big peak results in the instability of the cubic parent phase due to the Jahn—Teller effect.[30,31]Upon tetragonal distortions, these Co d andYd states around the Fermi level split, and there the peak in the total DOS then beomces smaller. Since the decrease of the states just right at the Fermi level lowers the energy of the system, the tetragonalD022phase is thus stabilized in all the three PM alloys. With Co andYsubstituting for Ga,this electronic structure mechanism becomes more and more effective. Then, in all the Gadeficient alloys with the PM ordering,with Co andYdoping,C′of theL21phase decreases whereasAincreases and upon tetragonal distortions,theD022phase becomes relatively more and more stable.

4. Summary

Using the first-principles EMTO-CPA method, we have systematically investigated the alloying and magnetic disordering effects on the site occupation, equilibrium properties,elastic property,and phase stability ofL21-andD022-Co2YGa(Y=Cr,V,and Ni)Heusler alloys. The main results are summarized as follows:

(1)At the ground FM state, both Co2CrGa and Co2VGa alloys possess theL21structure whereas Co2NiGa alloy is stabilized by theD022martensite. At the PM state, all the three stoichiometric alloys can show the martensitic transformation(MT) behavior and then have the tetragonal structure. Their evaluated crystal structure and lattice parameters,μtotandTCvalues,and elastic constants for both the austenite and martensite are in good agreement with the experimental and theoretical results.

(2) For the three stoichiometric alloys, with increasing the magnetic disordering degreey, theirC′of theL21phase decreases butAincreases,and upon tetragonal distortions the cubic phase becomes relatively more and more unstable. Fory ≥0.2,Co2CrGa and Co2VGa alloys thus can show the MT fromL21toD022as well. In comparison with Co2NiGa, in the two alloys the magnetic disordering effect on the relative stability of theD022phase is more dominant since at their FM state,μtotof theL21phase is much larger than that of theD022phase,which further accelerates the energy increase of the former relative to the latter in eachy ＞0.

(3)In off-stoichiometric alloys,the site preference is controlled by both the alloying and magnetic effects. From spinpolarized calculations,the excessive Ga atom always tends to take theYsublattice, whereas the excessive Co atom favors theYsite whenY=Cr,and the excessiveYatom prefers the Co site whenY=Ni. Calculated without spin-polarization,instead of being the normal site,the excessiveYatom changes to take the Co site whenY=Cr and the excessive Co atom changes to occupy the Ga site whenY=V, whereas in theY=Cr alloys,the excessive Co atom goes back to the normal site.

(4) In the Ga-deficient Co2Y(Ga1-xCox) and Co2Y(Ga1-xYx) alloys with the PM ordering, with increasingx(i.e,e/a),C′of theL21phase decreases butAincreases,whereas the relative electronic energy ΔEof theD022phase becomes lower and lower, which corresponds toTMincreasing withe/a. The same trends ofC′～x,A～x, ΔE～xare also found in these FMY=V and Ni alloys, resulting that the two groups ofY=V alloys withx ≥0.2 and 0.4,respectively,can occur with the MT also at the FM state. However,in the corresponding FMY=Cr alloys, their contrary trends are established, indicating that with the increase ofe/a, the RMT fromD022toL21is promoted and thenTMfor the RMT should decrease.

(5) Thex-dependent MT in Co2Y(Ga1-xCox) and Co2Y(Ga1-xYx)alloys is finally well explained by means of the Jahn—Teller effect at the PM state.At the FM state,it may originate from the competition between the austenite and martensite about their strength of the covalent banding between Co and Ga as well asYand Ga. With increasingx, it becomes relatively stronger and stronger in the austenite for theY=Cr alloys but in the martensite for theY=V and Ni alloys,which consequently promotes the RMT for the former alloys but the MT for the latter ones.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 12174269, 11674233 and 51301176), the China Postdoctoral Science Foundation(Grant Nos. 2013M530133 and 2014T70264), and the Natural Science Foundation of Liaoning Province, China (Grant Nos.2019-MS-287 and L201602672).