四面体十二点球定理推广研究的进展*

曾建国

(赣南师范大学 数学与计算机科学学院,江西 赣州 341000)

0 引言

人们将三角形九点圆定理推广至垂心四面体中,得到垂心四面体的两类“十二点球定理”.

第1类十二点球定理是法国数学家普鲁海(Prouhet)于1863年发现的.

命题1[1]垂心四面体中,垂心到四面体各顶点的连线的第1个三等分点、四面体各面的垂心和重心,共12点共球,其球心为外心与垂心连线的第2个三等分点,半径为四面体外接球半径的三分之一.

第2类十二点球定理是法国数学家坦佩莱(Temperley)与莱维(Lévy)于1881年发现的.

命题2[1]垂心四面体中,每个侧面三角形的三条高的垂足、6条棱的中点共12点共球,球心是四面体的重心.

20世纪末,随着垂心四面体的两类十二点球定理先后被国内研究者重新发现[2-3],人们又开始尝试将十二点球定理从垂心四面体推广至一般四面体中,并取得了可喜的进展.本文首先对四面体的十二点球定理的推广研究历程作一回顾,介绍近年来取得的研究成果,然后在此基础上对有关结论作进一步推广.

1 四面体的欧拉球面

到目前为止,对于四面体十二点球定理所作的推广研究,一般都是对四面体第1类十二点球定理(命题1)进行推广.这方面的研究工作主要是熊曾润教授完成的.2005年,熊曾润教授率先对垂心四面体十二点球定理进行了推广研究,建立了一般四面体的欧拉球概念并得到一般四面体中的12点共球(欧拉球)定理.以下约定:以点O为球心、长度R为半径的球面记作S(O,R).

定义1[4-5]设四面体A1A2A3A4的外接球面为S(O,R),若点W满足

(1)

则点W称为四面体A1A2A3A4的伪垂心;以线段OW的中点E为球心、R/2为半径的球面,称为四面体A1A2A3A4的欧拉球面,记作S(E,R/2).

其中,点E的向量表示为

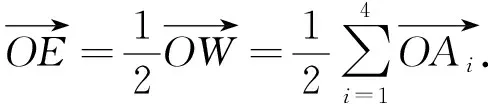
(2)

定义2[6]设四面体A1A2A3A4的外接球面为S(O,R),点Ej满足

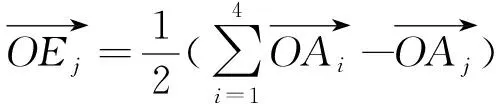
(3)

则以Ej为球心、R/2为半径的球面,称为侧面Δj的欧拉球面,记作S(Ej,R/2)(j=1,2,3,4).

根据上述定义,有

定理1[6]设四面体A1A2A3A4的外接球面为S(O,R),其伪垂心为W,则四面体A1A2A3A4的欧拉球面必通过12个特殊点,即:各顶点Aj与伪垂心W连线的中点Mj(j=1,2,3,4);各侧面Δj的欧拉球心Ej(j=1,2,3,4);过点Ej作直线与直线AjW垂直相交的垂足Dj(j=1,2,3,4).

2009年,熊曾润教授在全国第七届初等数学研究学术交流会(2009,深圳)发表了令人叹为观止的“四面体36点共球定理”,引起国内学者的广泛关注.熊教授在他的论文中还将这个定理称为“中国36点球定理”[6],可见熊教授对他的这一成果的钟爱程度.

图1

定理2[6-7]设四面体A1A2A3A4的外接球面为S(O,R),其伪垂心为W,其侧面Δj的欧拉球心为Ej,过点Ej作直线与直线AjW垂直相交于Dj,且设此直线交球面S(O,R)于Bj、Cj两点(如图1),则ΔAjBjCj的九点圆必在四面体A1A2A3A4的欧拉球面S(E,R/2)上(j=1,2,3,4).

在定理2中,由于每个三角形的九点圆通过9个特殊点,因此这个定理告诉我们:四面体的欧拉球面通过4×9=36个特殊点.

2 四面体的k+1号球面

继四面体欧拉球面概念及性质的提出后,熊曾润教授将命题1与定理1中的十二点球又统一推广至四面体的k+1号球面.

熊教授首先建立了四面体的k号心及四面体的k+1号球面概念.

定义3[8]设四面体A1A2A3A4的外心为O,对于任一给定的正整数k,顶点Aj所对的侧面记作Δj(j=1,2,3,4),

(4)

则称P为四面体A1A2A3A4(关于点O)的k号心.

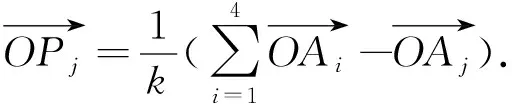
(5)

则称Pj为四面体A1A2A3A4的侧面Δj(关于点O)的k号心.

根据上述定义,可以推得

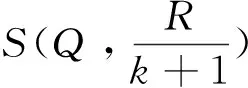
容易验证:在定理3中令k=1即得定理1.

在定理3中令k=2就得

推论1设P为四面体A1A2A3A4的2号心(欧拉球心),则四面体A1A2A3A4的3号球面S(Q,R/3)必通过12个特殊点,即:PAj的第1个三等分点Mj(即PMj∶MjAj=1∶2,j=1,2,3,4);各侧面Δj的3号心Qj(即Δj的重心,j=1,2,3,4);过点Qj作直线与直线AjP垂直相交的垂足Hj(j=1,2,3,4).

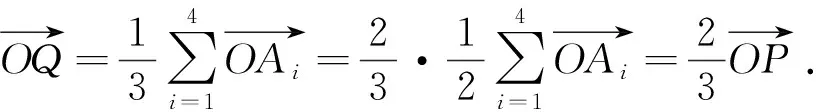
由此可知,命题1、定理1都是定理3的特例,而定理3是命题1与定理1的统一推广.

按照前文定义的概念(定义4)来表述,定理3实质上已将四面体12点共球性质从四面体的2号球面(定理1)和3号球面(推论1)推广至四面体的k+1号球面.这似乎应该算是垂心四面体第1类十二点共球定理的“终极”推广!其实不然,熊曾润教授还将定理3作了进一步的推广.

熊曾润教授将四面体的k号心、k+1号球面概念推广至更一般化的四面体的“广义k号心”“广义k+1号球面”,即

定义5[10]设四面体A1A2A3A4的外接球面为S(O,R),H是异于外心O的任一给定的点,对于任一给定的正整数k

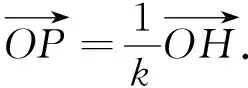
(6)

则称P为四面体A1A2A3A4的广义k号心.

(7)

根据上述定义,可得

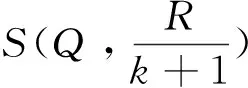
熊曾润先生对十二点球定理的推广研究进程层层递进、不断打破原有的思维限制,不愧为是数学创新研究的经典范例.

3 四面体的20点共球定理

对于垂心四面体第1类12点共球定理的推广研究还有其他方式,这里也作一介绍.

2010年,耿恒考得到了一般四面体20点共球定理.原文的表述是

命题3[11]四面体各面三角形的重心、经过顶点与垂心注1的外接球的弦被垂心分成的两条线段的三等分点(靠近垂心)、经过垂心且垂直于一个面的外接球的弦被垂心分成的两条线段的三等分点(靠近垂心),这20个点共球,其半径等于外接球半径的1/3,球心是重心与垂心连线的三等分点(靠近重心).

注1命题3中所说四面体的“垂心”其实就是四面体的欧拉球心,也被称为四面体的蒙日(Monge)点(详见文[1]).

因此,命题3实质上是在推论1中共球12点的基础上增加了另外8个点(见命题3′).为进一步推广命题3的结论,我们先证明命题3与下面的命题3′等价.

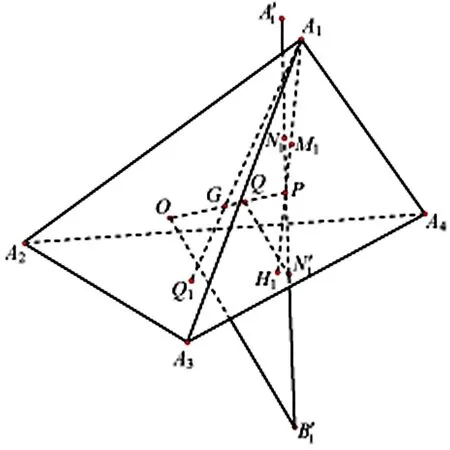
图2

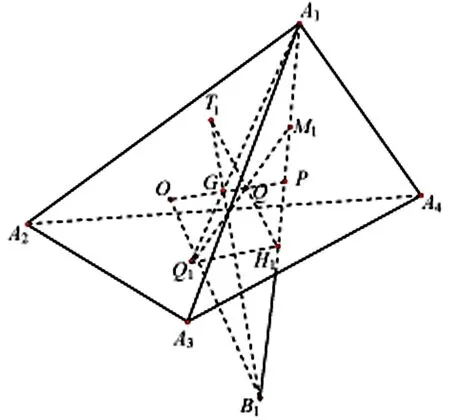
图3

证明根据推论1,只需证命题3'中新增的8个点在球面S(Q,R/3)上.

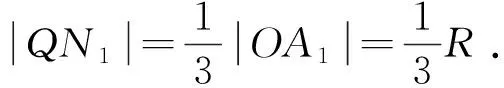
为了说明命题3′与命题3等价,还需证明命题3′中点Hj是四面体外接球过Aj、P的弦被P分成的两线段之一(例如图3中线段PB1)的三等分点(靠近P).

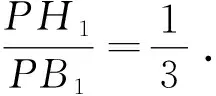
根据定理3知,H1在球面S(Q,R/3)上,即|QH1|=1/3R.

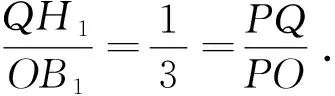
由此可知,命题3′可推广为更一般的(证略).

4 四面体的32点共球定理

在四面体的3号球面S(Q,R/3)上,还可以继续挖掘出其他的特殊点.

定理6设P、Q、G分别为四面体A1A2A3A4的欧拉球心、3号心、重心,直线AjP与四面体外接球面的另一交点为Bj,PBj的三等分点(靠近P)为Hj(j=1,2,3,4).则直线HjQ与BjG的交点Tj(j=1,2,3,4)在四面体A1A2A3A4的3号球面S(Q,R/3)上.

证明如图3,设H1是PB1的三等分点(靠近P),直线H1Q与B1G的交点T1.欲证T1在球面S(Q,R/3)上,只需证|QT1|=1/3R.

根据前面(命题3′)的证明知QH1∥OB1,则ΔQGT1～ΔOGB1.

证明根据前面诸命题知,Mj与各侧面Δj的重心Qj均在3号球面S(Q,R/3)上,且QjMj是该球面的直径(j=1,2,3,4).

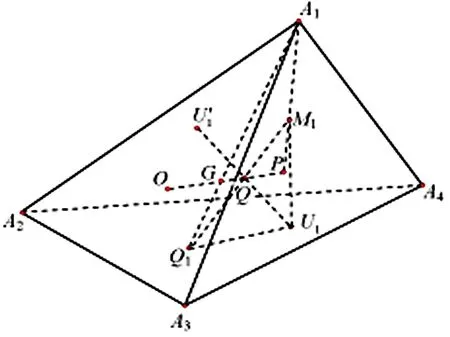
图4

如果在命题3′的共球20点的基础上再加上定理6、定理7中的12个点,就得下面的四面体32点共球定理.

定理8(四面体32点共球定理)设P、Q、G分别为四面体A1A2A3A4的欧拉球心、3号心、重心,则四面体A1A2A3A4的3号球面S(Q,R/3)必通过32个特殊点,即:

5 后续研究的问题与课题

对四面体第1类十二点球定理还可以作进一步的推广研究工作.一方面,可以仿效定理3、定理4那样,将定理6-8(及命题3′、命题4)进一步推广至四面体的k+1号球面.有兴趣的读者可以尝试.

另一方面,对已有结论进一步推广至高维空间也是很有意义的.例如,文献[12]已将“另类的十二点球定理”(即本文定理7中“Mj、Qj、Uj(j=1,2,3,4)在3号球面S(Q,R、3)上”)推广至n维单形中;已开展的其他高维推广研究工作还有:将四面体中的结论推广至球内接多面体[13]、或推广至n维单形[14-15]、n维共球有限点集中[16-18].

而垂心四面体第2类十二点球定理是否可以进一步推广则有待于人们继续探索研究.