基于负刚度惯容型非线性能量汇的整星振动抑制*

高原 张振 方勃

(沈阳航空航天大学 航空宇航学院, 沈阳 110136)

引言

目前,国际上将总质量介于1kg至10kg之间的卫星称为纳米卫星,总质量介于11kg至100kg的卫星称为微卫星[1,2].1990年5月,美国使用“侦察兵”火箭发射了两颗6.8kg的“多路通信卫星”.自此,诸多卫星产业大国争相开展了对微小卫星的开发研究[3-5].

航天器在发射过程中会受到来自结构内部和外界环境的各种形式的振动干扰,强烈的振动会导致航天器中电子设备仪器的性能失效从而不能正常工作,甚至会破坏航天器结构,造成巨大损失.因此,改善航天器的振动环境是提高卫星发射安全性和可靠性的关键[6].卫星隔振最早是由美国CSA公司应空军研究室要求在1993年开展了对整星隔振器的研究[7,8].Johnson在1996年提出被动整星控制平台,并取得很好减振效果[9].王晓雷等人在被动隔振的基础上加入主动控制,改进系统的低频隔振性能,实现全频带隔振[10].

非线性能量汇(Nonlinear energy sink)最早是由Vakakis在2001年提出[11].NES具有吸振频带宽、快速高效的能量转移等显著优点[12-16].常见的非线性能量汇主要有:杠杆式非线性能量汇、轨道式非线性能量汇、限幅式非线性能量汇等.这些研究表明非线性能量汇具有广泛的应用前景.

惯容器最早是由Smith在2002年提出[17].惯容器具有两个连接终端,与质量都可以作为惯性元件,但与质量不同的是,惯容器可以提供比其质量大得多的惯性系数且可以调节.将惯容器集成到非线性能量汇中可以适当地增强其减振效果,然而带有惯容器的非线性能量汇仍有质量大的缺陷[18].非线性能量汇中的质量块可以完全用惯容器替代,这种新型惯容型非线性能量汇几乎不引入附加质量,克服了传统非线性能量汇的大质量缺陷,且具有更高的减振性能[19].

负刚度最早是由英国工程师Molyneux在1957年提出[20].Molyneux使用两个横向弹簧元件形成了负刚度结构.而后大部分学者基于负刚度理论,将负刚度弹簧元件与正刚度弹簧元件相结合形成具有高静态低动态刚度特性的准零刚度隔振器[21,22].引入负刚度元件可以强化减振器的减振效果.Wu等[23]提出了一种新型负刚度磁弹簧(MS-NS)隔振器,并与没有负刚度磁弹簧的隔振器进行比较,实验结果表明,带有负刚度磁弹簧隔振器可以降低系统固有频率并减小共振幅值,实现更好的减振效果.Zhou等[24]提出了一种应用于浮板轨道的负刚度动力吸振器(NSDVA)并与传统的Voigt型动力吸振器相比,带有负刚度的动力吸振器具有更好的减振效果.

本文提出了一种带有负刚度的惯容型非线性能量汇应用于整星系统的振动抑制.同时,比较了不同激励幅值下,负刚度惯容型非线性能量汇、惯容型非线性能量汇和正刚度惯容型非线性能量汇的减振效果,讨论了负刚度元件对减振性能的影响.基于牛顿第二定律推导出耦合系统的动力学方程.应用谐波平衡法得到系统稳态响应的近似解析解,并通过Runge-Kutta法得到系统的数值解验证解析解的正确性.此外,讨论了负刚度惯容型非线性能量汇的参数对其减振效果的影响.本项研究将促进和拓宽负刚度和惯容型非线性能量汇的实际工程应用.

1 负刚度惯容型非线性能量汇组合减振系 统动力学建模

图1为耦合负刚度惯容型非线性能量汇的整星振动系统,其中整星系统简化为二自由度线性振子[25].图中,m1,c1和k1分别为卫星的质量,阻尼和线性刚度.m2,c2和k2分别为卫星适配器的质量,阻尼和线性刚度.b为惯容器惯性质量,其两终端的作用力与两终端的相对加速度成正比.惯容器的惯性质量远远大于其自身重量,因此数学建模过程中,惯容器的质量可以忽略不计[17].c3为负刚度惯容型非线性能量汇的阻尼.负刚度惯容型非线性能量汇的负刚度和立方非线性刚度由两个预压缩的横向线性弹簧实现.k3为横向弹簧刚度值,L0为弹簧初始长度.系统处于静平衡时,横向弹簧处于水平位置,此时弹簧长度为LH.x1,x2和x3分别为卫星,卫星适配器和惯容器的位移.系统的外激励为谐波位移激励xe=Acos(ωt),其中,A和ω分别为位移激励的幅值和频率.

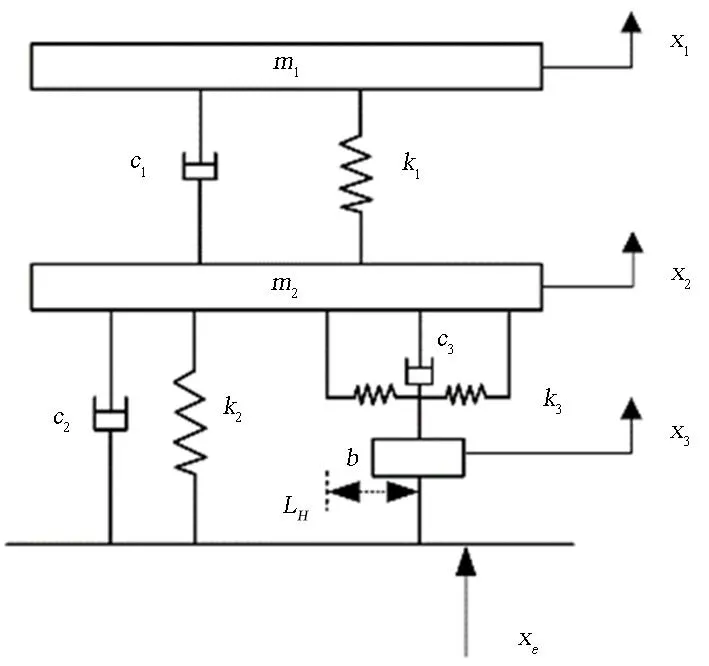
图1 耦合负刚度惯容型非线性能量汇的整星振动系统Fig.1 Whole-spacecraft vibration system coupled with negative stiffness inertial nonlinear energy sink

横向弹簧在垂直方向上的非线性弹性力F推导如下:

(1)

由泰勒公式展开可得:

(2)

(3)

非线性弹性力F与位移差(x2-x3)的精确关系曲线和泰勒展开近似关系曲线如图2所示.从图中可以看出,在泰勒展开项数为三阶的时候,就可以满足对精度的需求.

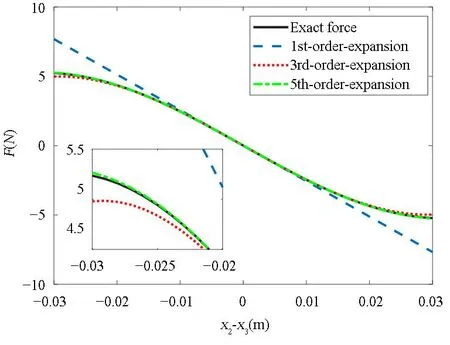
图2 非线性弹性力泰勒级数展开曲线Fig.2 Nonlinear elastic force Taylor series expansion curve

由牛顿第二定律推导出耦合负刚度惯容型非线性能量汇的整星系统的动力学方程为

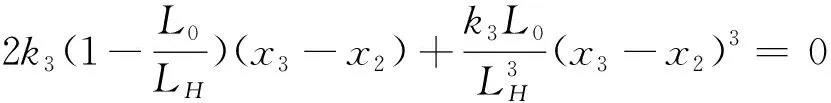
(4)

经过无量纲化处理,可得:

(5)

无量纲变量和参数为

(6)

2 稳态幅频响应

2.1 谐波平衡方法求解

由于系统方程中只包含立方非线性项,故而只考虑奇次谐波项,忽略偶次谐波项的影响.基于谐波平衡方法,设整星系统的稳态响应位移解的形式为

b1,2i+1·sin[(2·i+1)·Ω·τ]}

b2,2i+1·sin[(2·i+1)·Ω·τ]}

b3,2i+1·sin[(2·i+1)·Ω·τ]}

(7)

谐波平衡方法为近似解析方法,其假设解取的谐波阶数越多,得到的近似解析解就越精确.然而,阶数过多,得到的系数方程就会越多,从而使得计算量大大增加.在这里,以一阶谐波假设解为例给出求解过程.令i=0,则式(7)将变为

u1=a11cos(Ωτ)+b11sin(Ωτ)

u2=a21cos(Ωτ)+b21sin(Ωτ)

u3=a31cos(Ωτ)+b31sin(Ωτ)

(8)

将式(8)代入式(7)中,整理谐波系数方程组可得到一组非线性代数方程组.

(9)

-Ωξ1b11+Ωξ1b21-Ω2a21λ2+Ωξ2b21+

Ωξ1a11-Ωξ1a21-Ω2b21λ2-Ωξ2a21+

b21β2+b21α-b31α-b11+b21-

(10)

(11)

求解代数方程组可以得到谐波系数的常数值.将所得到的值代入到谐波假设解,可以得到位移的时域响应.通过提取不同激励频率下位移时域响应的幅值,可以得到位移的幅频响应曲线.

2.2 数值验证

考虑到非线性能量汇中采用的是立方非线性,因此,谐波平衡假设解只保留1阶和3阶谐波,忽略偶次和高阶谐波的影响.由Runge-Kutta数值方法求得系统的时间历程,时间步长设置为一个周期T的0.01倍.然后从时间历程中的稳态响应部分提取出系统的响应幅值.控制激励频率正向增大和反向减小,通过打点的方式,可以得到数值解的正向和反向扫频幅频响应曲线,用以验证谐波平衡解的精确性.

系统仿真参数如表1所示.图3(a)、图3(b)分别为位移激励A为0.0018m时的耦合负刚度惯容型非线性能量汇的整星系统的一阶主共振和二阶主共振的解析解与数值解对比.从图中可以看出解析解和数值解的对比具有较好的重合度.

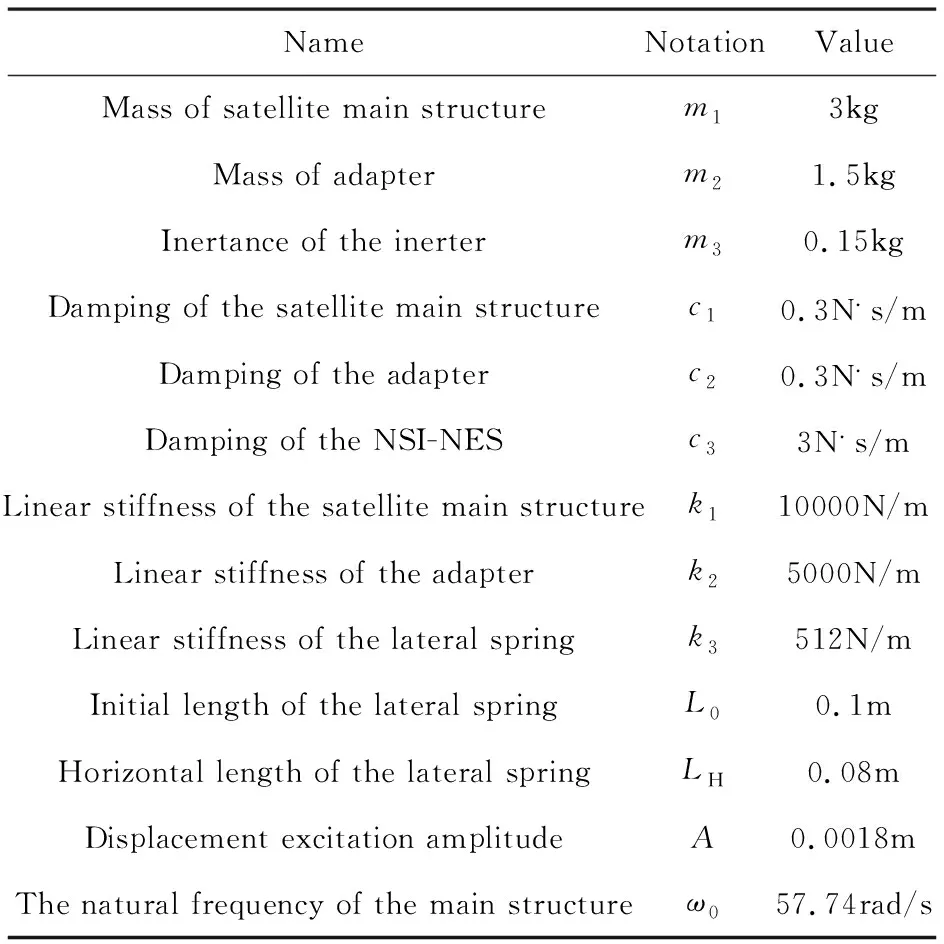
表1 系统量纲参数

(a)一阶主共振

3 减振性能比较

本节对比研究负刚度惯容型非线性能量汇(NSI-NES)、正刚度惯容型非线性能量汇(PSI-NES)和惯容型非线性能量汇(I-NES)的减振性能.

未控系统位移响应的最大幅值记为Au,控制系统的位移响应的最大幅值记为Ac,控制系统的最大幅值减少百分比为

(12)

相同质量下,激励幅值为A=0.0014m 、A=0.0016m、A=0.0018m时的负刚度惯容型非线性能量汇、惯容型非线性能量汇和正刚度惯容型非线性能量汇的减振效果分别如图4～图6所示.其中,图(a)、图(b)分别为耦合负刚度惯容型非线性能量汇、惯容型非线性能量汇、正刚度惯容型非线性能量汇的整星系统一阶主共振和二阶主共振的减振效果的对比图.

图4 励幅值A=0.0014m时减振效果:(a)一阶主共振;(b)二阶主共振Fig.4 Vibration damping effect when excitation amplitude A=0.0014 (a) First-order primary resonance;(b) Second-order primary resonance

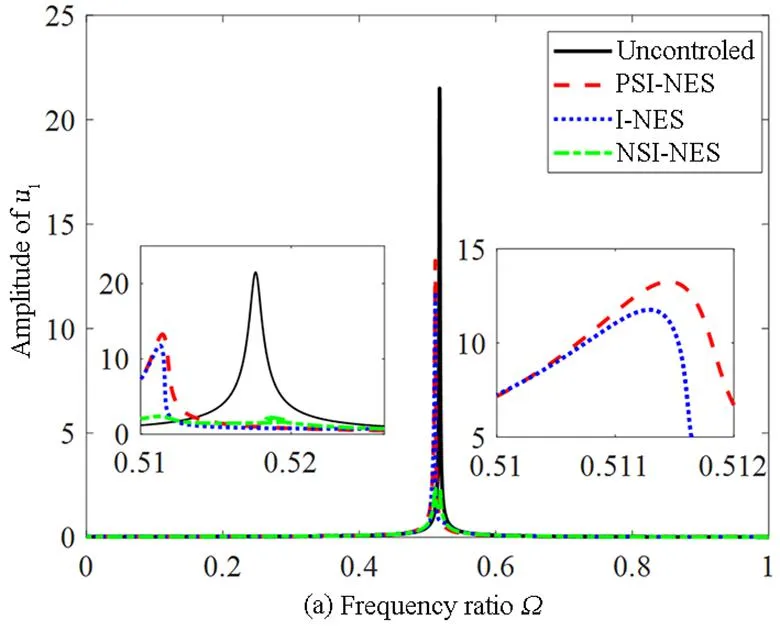
图5 励幅值A=0.0016m时减振效果:(a)一阶主共振;(b)二阶主共振Fig.5 Vibration damping effect when excitation amplitude A=0.0016m: (a) First-order primary resonance;(b) Second-order primary resonance

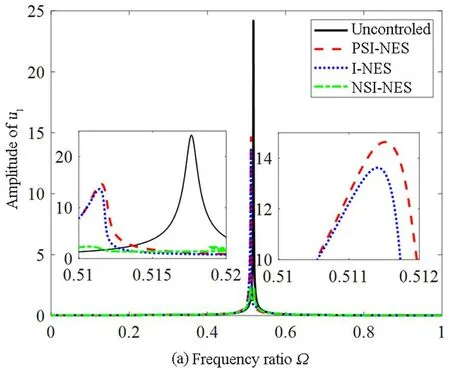
图6 励幅值A=0.0018m时减振效果:(a)一阶主共振;(b)二阶主共振Fig.6 Vibration damping effect when excitation amplitude A=0.0018m: (a) First-order primary resonance;(b) Second-order primary resonance

激励幅值A为0.0014 m时,负刚度惯容型非线性能量汇的减振百分比达到了87.86%,而在相同情况下的惯容型非线性能量汇的减振百分比则为48.35%,正刚度惯容型非线性能量汇的减振百分比为43.3%.在一阶主共振中,激励幅值A为0.0016m时,负刚度惯容型非线性能量汇的减振百分比达到了89.08%,而在相同情况下的惯容型非线性能量汇的减振百分比则为45.4%,正刚度惯容型非线性能量汇的减振百分比却为39.6%.激励幅值A为0.0018m时,负刚度惯容型非线性能量汇的减振百分比达到了90.72%,而在相同情况下的惯容型非线性能量汇的减振百分比则为43.6%,正刚度惯容型非线性能量汇的减振百分比却为40.3%.通过对比可以发现,在相同激励幅值下,一阶主共振中的负刚度惯容型非线性能量汇的减振效果要远优越于惯容型非线性能量汇和正刚度惯容型非线性能量汇.

激励幅值增大,一阶主共振中的负刚度惯容型非线性能量汇和正刚度惯容型非线性能量汇的减振效果越好.随着激励幅值的增大,一阶主共振中的惯容型非线性能量汇的减振效果,先降低后增高.从图4(b)、5(b)、6(b)中可以看出,在二阶主共振中,三者的减振性能都达到较好减振效果,也可以看出在二阶主共振中,正刚度惯容型非线性能量汇的减振效果要略高于惯容型非线性能量汇,惯容型非线性能量汇的减振效果要略高于负刚度惯容型非线性能量汇.综合考虑,随着激励幅值的增大,负刚度惯容型非线性能量汇的减振效果要优于惯容型非线性能量汇和正刚度惯容型非线性能量汇.

4 负刚度惯容型非线性能量汇的参数影响

4.1 惯性质量的影响

惯性质量对主系统幅频响应曲线的影响如图7所示.从图7中可以看出,随着惯性质量值的增大,主结构一阶和二阶幅频响应曲线的峰值均呈现出减小趋势,最后归于平稳.

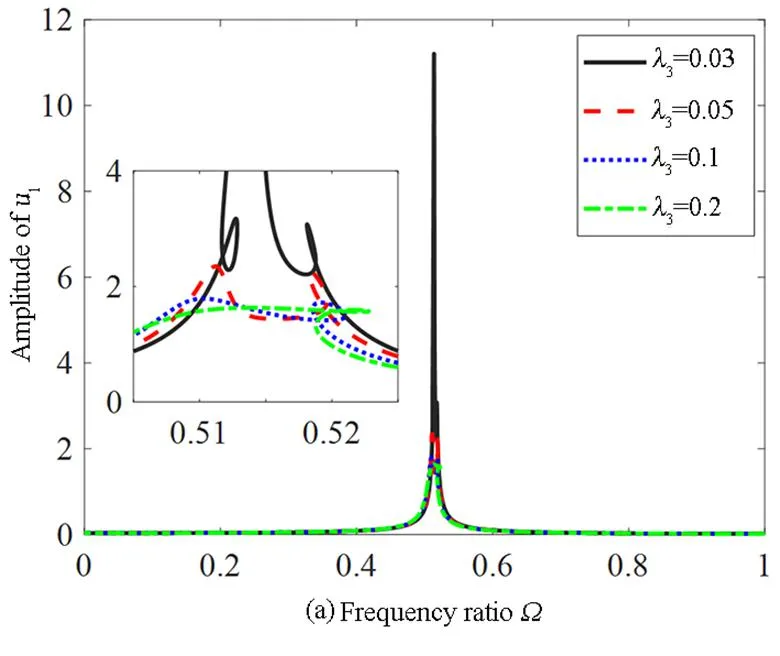
图7 不同惯性质量下整星系统的幅频响应曲线:(a)一阶主共振;(b)二阶主共振Fig.7 Amplitude-frequency response curves of whole-spacecraft system under different inertial masses (a) First-order primary resonance;(b) Second-order primary resonance

4.2 负刚度的影响

负刚度对主系统幅频响应曲线的影响如图8所示.在确保立方非线性刚度值不变的情况下,负刚度值可通过同时调节横向弹簧水平长度值LH和弹簧线性刚度值k3来进行改变.

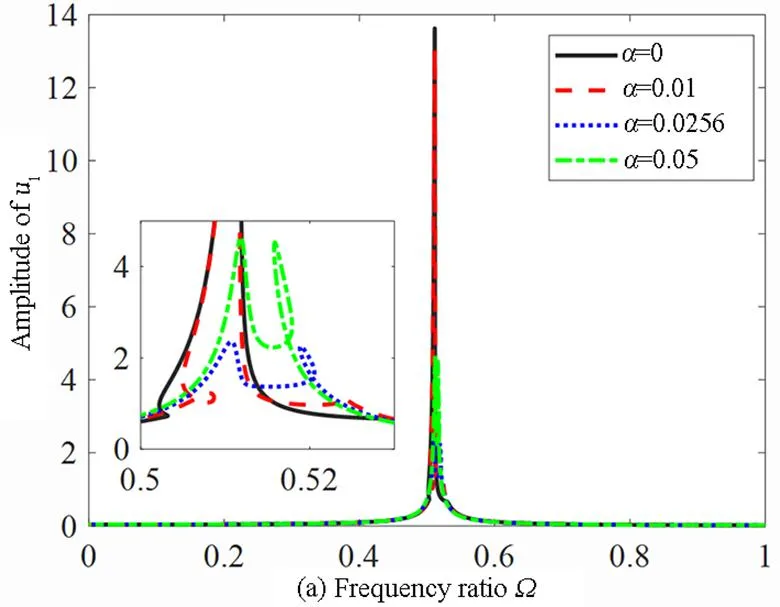
图8 不同负刚度下整星系统的幅频响应曲线:(a)一阶主共振;(b)二阶主共振Fig.8 Amplitude-frequency response curves of whole-spacecraft system under different negative stiffnesses (a) First-order primary resonance;(b) Second-order primary resonance

从图8(a)中可以看出,在一阶主共振中,当负刚度的值为0(L0=LH)时,系统的幅频响应的峰值最大.随着负刚度绝对值的增大,主结构幅频响应曲线的峰值呈现出先减小后增大的趋势.在α从0到-0.0256的区间,主结构位移有极为明显的骤降趋势.从图8(a)也可以看出负刚度存在一个最优值使得主结构幅频响应曲线的峰值最小.当负刚度α≈-0.0256时,主结构幅频响应曲线的峰值最小.从图8(b)中可以看出,在二阶主共振中,随着负刚度绝对值的增大,主结构幅频响应曲线的峰值呈现增大的趋势,且向左移动.综合考虑第一阶主共振和第二阶主共振的振动,负刚度α=-0.0256时,负刚度惯容型非线性能量汇的减振效果较好.

4.3 立方非线性的影响

立方非线性对主系统幅频响应曲线的影响如图9所示.在确保负刚度值不变的情况下,立方非线性刚度值可通过同时调节横向弹簧水平长度值LH和弹簧线性刚度值k3来进行改变.

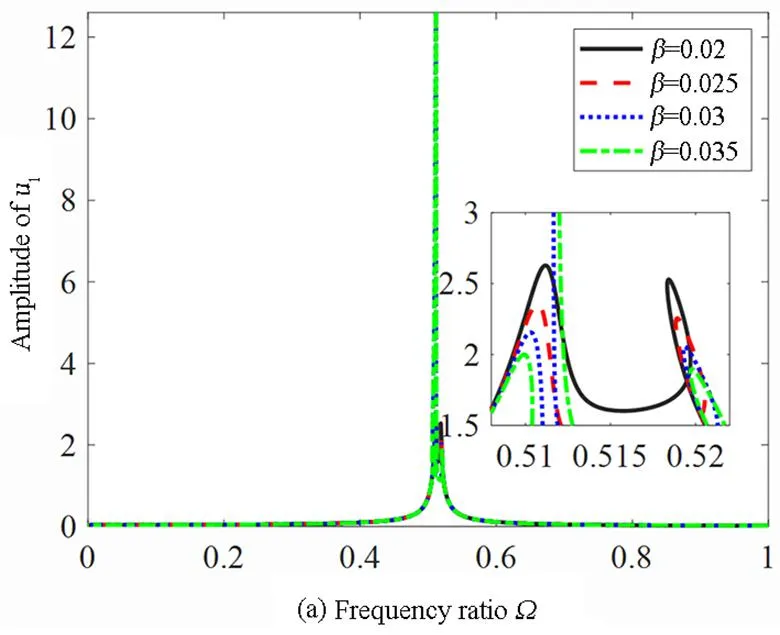
图9 不同非线性刚度下整星系统的幅频响应曲线:(a)一阶主共振;(b)二阶主共振Fig.9 Amplitude-frequency response curves of whole-spacecraft system under different nonlinearity stiffness (a) First-order primary resonance;(b) Second-order primary resonance

从图9(a)中可以看出,在一阶主共振中,随着立方非线性刚度的增大,主结构幅频响应曲线的峰值呈现出先减小再增大的趋势.因此,立方非线性刚度存在一个最优值使得主结构幅频响应曲线的峰值最小.从图9(b)中可以看出,在二阶主共振中,随着立方非线性数值的增大,主结构幅频响应曲线的峰值呈现向下的趋势但影响较小.综合考虑第一阶主共振和第二阶主共振的振动,立方非线性刚度β4=0.03时,负刚度惯容型非线性能量汇的减振效果较好.

4.4 阻尼的影响

阻尼对主结构幅频响应曲线的影响如图10所示.从图10(a)中可以看出,在一阶主共振中,随着阻尼的增大,主结构幅频响应曲线的峰值也逐渐增大.从图10(b)中可以看出,在二阶主共振中,随着阻尼数值的增大,主结构幅频响应曲线的峰值呈现向下的趋势.综合考虑第一阶主共振和第二阶主共振的振动,当ζ3=0.0173时,负刚度惯容型非线性能量汇的减振效果较好.

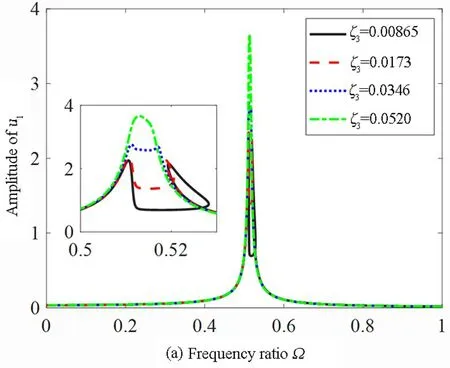
(a)一阶主共振

4.5 阻尼和立方非线性刚度共同影响

通过负刚度惯容型非线性能量汇参数对幅频响应曲线的影响了解到,参数变化对系统第一阶主共振响应的影响较大,因此参数研究只考虑第一阶主共振.对于不同的负刚度α=0、-0.0256和-0.05,当负刚度惯容型非线性能量汇的阻尼和立方非线性同时变化时,主结构的幅频响应曲线的最大幅值变化的二维等高线图如图11所示.随着阻尼和立方非线性刚度参数增大,减振效果得到明显改善.图11(a)中,当立方非线性和阻尼同时变化时,减振性能最优区域形成“山谷”,在该区域最大幅值接近11.当负刚度值为-0.0256时,如图11(b)所示,“山谷”区域明显增大了,最大幅值的最优值也显著降低了,约为8.当负刚度值为-0.05时,如图11(c)所示,最大幅值的最优值约为6.比较发现,随着负刚度值绝对值的增大,实现的减振效果越好.

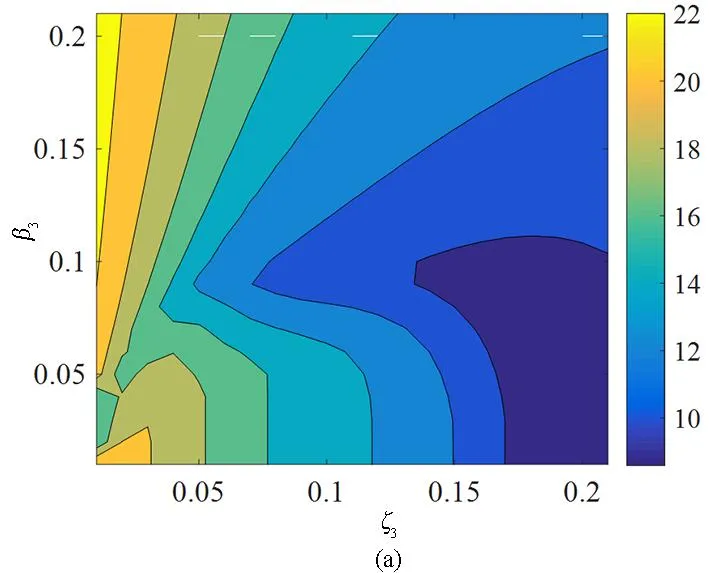
图11 负刚度惯容型非线性能量汇的阻尼和立方非线性同时变化对主结构频响最大幅值的影响(a) α=0;(b) α=-0.0256;(c) α=-0.05Fig.11 The influence of the simultaneous change of damping and cubic nonlinearity of negative stiffness inertial nonlinear energy sink on the maximum amplitude of the frequency response of the main structure(a) α=0;(b) α=-0.0256;(c) α=-0.05

5 结论

本文使用了一种新型负刚度惯容型非线性能量汇对整星系统进行减振,基于谐波平衡法求解系统的幅频响应曲线,讨论了负刚度惯容型非线性能量汇的减振效果,并对其参数进行了分析和优化.以下是具体结论:

(1) 负刚度惯容型非线性能量汇应用到整星系统中可以实现高效的振动抑制,其减振性能随着激励幅值的增加而增大.

(2) 参数研究表明,在合适区间范围内,负刚度非线性能量汇的参数变化对一阶主共振影响较大,当其他参数是定常数时,负刚度、立方非线性、阻尼都具有最优值,而惯性参数随其数值增大,减振效果增强到一定程度后趋于稳定.

(3) 参数优化显示,在合适区间范围内,负刚度非线性能量汇的负刚度绝对值越大,可以实现的减振效果越好.