一种基于四元数的空间后方交会全局收敛算法
龚 辉,姜 挺,江刚武,陈密密
1.信息工程大学测绘学院,河南郑州450052;2.61512部队,北京100088
1 引 言
摄影测量学中惯用的空间后方交会解法是把成像时的姿态采用欧拉角描述,对共线条件方程进行线性化,然后通过一定数量的地面控制点及像片上对应的像点,利用最小二乘原理进行迭代求解[1]。该算法对外方位元素的初值要求很高,当初值不好时,迭代不收敛。同时该算法对像片获取的传感器平台飞行质量要求比较高,其姿态角不能太大,一般为垂直摄影。然而随着传感器技术的发展,姿态控制水平的提高,很多影像都是大倾角像片,如无人机、飞艇等获取的像片及近景摄影所得到的影像。对于这类像片的空间后方交会,实践表明惯用的算法由于无法获取大倾角情况下良好的外方位元素初值而求解失败。
为有效解决空间后方交会对外方位元素良好初值依赖的问题,文献[2]提出一种利用多种几何特征进行求解的线性算法,文献[3—4]各自提出只利用三个控制点进行后方交会的解析算法,文献[5]提出利用四个相关点进行后方交会的求解方法,文献[6—7]分别提出利用点、线进行位置和姿态估计的线性解法。上述算法都是直接计算,无需外方位元素的初值,但是这些算法仅仅在只有少量控制点等情况下有效,当控制点较多时,求解非常复杂。为求解任意控制点情况下的外方位元素,文献[8—9]提出一种基于单位四元数的无初值依赖空间后方交会算法。该算法是一种迭代算法,思路上与传统算法类似,试验表明对外方位元素的初值无特殊要求,但该算法没有从理论上对此进行证明。文献[10]也提出一种基于四元数的空间后方交会算法,但该算法的求解需要首先迭代解算出摄站到控制点距离,仍然需要良好的初值。
全局收敛算法,即无论迭代从何处出发,均能收敛到最终结果,表明计算与迭代初值无关,该类算法在计算机视觉领域中应用较多。文献[11]提出一种从视觉图像中估计姿态的正交迭代算法。该算法具有全局收敛的性质,然而在利用奇异值分解求解旋转矩阵时容易出现矩阵行列式值为-1的情况,导致求解结果不准确。文献[12]也提出一种全局收敛条件下的结构与运动估计快速算法。若将上述算法直接用于摄影测量空间后方交会,还存在一些问题,主要原因是二者的坐标系统不一致,且旋转矩阵的计算容易产生错误结果。基于此,本文借鉴上述全局收敛思想,结合四元数在摄影测量中的良好应用[8-9,13],提出一种基于四元数的空间后方交会全局收敛算法,并从理论上证明其全局收敛的特性。最后通过试验比较,验证了本文算法的正确性和优越性。
2 空间后方交会全局收敛算法的基本原理
本文全局收敛算法的基本原理是将中心投影的共线条件方程转化为绝对定向方程和正交投影变换公式,以此来建立数学模型和误差函数进行求解,并在求解过程中应用四元数描述摄影姿态。该算法无须对共线条件方程进行线性化,是一种非线性方程的迭代算法。
2.1 四元数及其三维旋转表达形式
四元数是形如˙q=q0+iq1+jq2+kq3的超复数[14],其中 i,j,k为虚数单位,且满足 i2=j2= k2=-1,jk=-kj=i,ki=-ik=j,ij=-ji= k。可以将四元数分解成标量q0和矢量 q,即˙q= q0+q,其中 q=iq1+jq2+kq3。
四元数有自己的运算规则[8],利用四元数的矢量形式可将两个四元数的乘积写为矩阵形式

式中

文献[8]对四元数的运算及其表达旋转矩阵作了详细论述,本文不再重复,直接给出用四元数表达的三维旋转形式及其对应的旋转矩阵M,如式(1)所示

由式(1)的旋转矩阵求取摄影测量中惯用的欧拉角如式(2)所示。
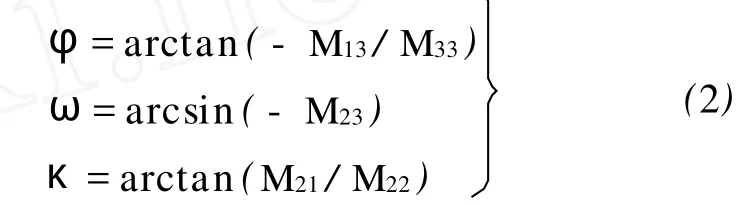
2.2 数学模型
采用四元数描述影像姿态时,像片的外方位元素变为(XS,YS,ZS,q0,q1,q2,q3),此时利用摄影测量理论[1],可得基于四元数的共线条件方程为
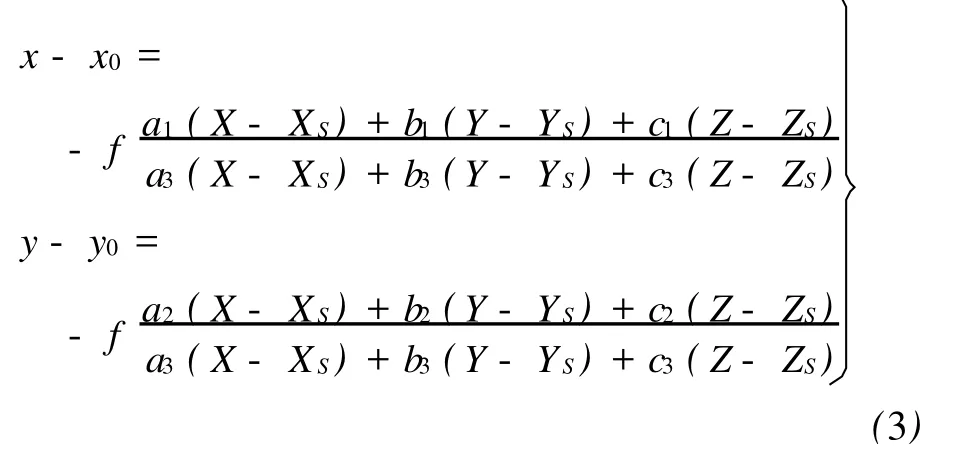
式中,(x0,y0,f)为像片内方位元素;(x,y)为像点坐标;(X,Y,Z)为地面坐标;(XS,YS,ZS)为摄站位置;ai,bi,ci,i=1,2,3由式(1)确定。
将式(3)改写为以下形式

式中
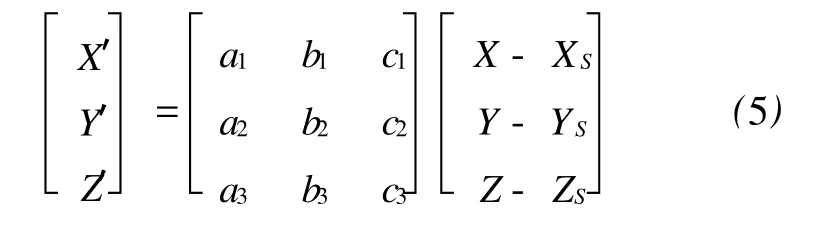
将式(5)表示为矢量形式

式中,t=-MrS;r′=(X′,Y′,Z′)T;r=(X,Y, Z)T;rS=(XS,YS,ZS)T。
此时共线条件方程式(4)变为

式中,v=(x-x0,y-y0,-f)T;r′(3)为矢量 r′的第三个分量。
由式(7)可以看出,矢量v既是坐标原点与投影点(X′,Y′,Z′)连线的方向向量,又是坐标原点与像点连线的方向向量,即投影点r′与像点共线。根据正交投影的性质,r′=(X′,Y′,Z′)T在方向v上的正交投影与其自身相等[11-12],则

式(6)与绝对定向方程具有相似的形式[1,13],只不过比例因子为1,因此,摄影成像过程可以分解为先对地面点(X,Y,Z)进行旋转平移,得到投影点(X′,Y′,Z′),再对投影点(X′,Y′,Z′)进行正交投影,得到像点坐标(x,y)。
2.3 误差函数
借鉴文献[11]中的目标空间误差,建立本文全局收敛算法的误差函数。由于数据点误差的影响,对每一个控制点,等式(8)两边存在偏差,即

式中,i为点号。
因此,按最小二乘原理进行空间后方交会就是要使式(9)中所有控制点误差的平方和最小,即使式(10)的误差函数最小

式中,M为包含姿态四元数的旋转矩阵,且MTM= I,ri为控制点地面坐标,rS为摄站位置,n为点数。
3 空间后方交会全局收敛算法的实现
3.1 摄站位置计算
式(10)即为本文全局收敛算法的误差函数。为求解外方位元素,将式(10)展开,可得


式中,Hi=(I-Vi)T(I-Vi)
当旋转矩阵 M已知时,E(M,rS)转化为E(rS),即式(11)仅为 rS的函数,对其求导数,可得

根据高等数学中的极值定理,要使式(11)最小,只需上述导数为0即可
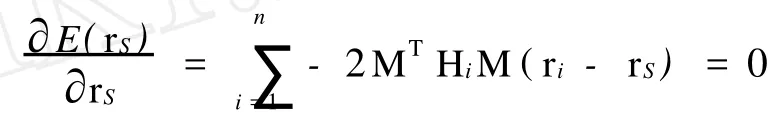
求解可得

式(12)即为利用旋转矩阵计算摄站位置的计算公式。当M已知时,rS为关于M的最优解。
3.2 姿态四元数计算
由式(12)可知,摄站位置 rS是旋转矩阵M的函数,代入式(10),可得到误差函数为只包含旋转矩阵M的函数,即

式中,T=-MrS(M);r′(M)=M(ri-rS(M))
此时,式(10)的误差函数 E(M,rS)最小转化为式(13)的 E(M)最小。该表达式与绝对定向的表达式[1,13]有类似的形式。本文利用四元数直接对式(13)进行求解[13,15],得到姿态四元数。按绝对定向求解方法需对坐标 ri、Vir′i(M)进行重心化,同时令 rE,i=Vir′i(M),则式(13)变为

将式(14)展开[13]




将上式展开,得到


于是求解姿态四元数只需在四元数域求解˙q,使得 F最大时,E最小即可。
利用四元数的运算法则有[8]
上式代入前文四元数乘积的矩阵为

继续推导,可得

式中,

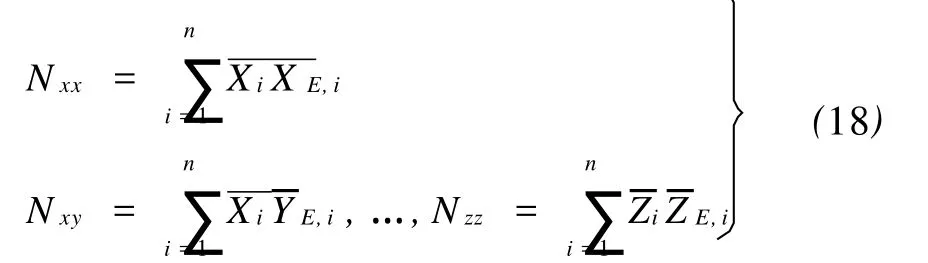
由于矩阵N为实对称矩阵,式(17)达到最大值的条件是姿态四元数的取值˙q为矩阵N的最大特征值所对应的特征向量[13]。求出四元数 ˙q后,便可按式(1)求得旋转矩阵M。
3.3 迭代过程
由于摄站位置的计算依赖于旋转矩阵M,而构成旋转矩阵的姿态四元数的计算又依赖于摄站位置,因此,需要反复迭代求解。当控制点个数n≥3时,预先任意给定旋转矩阵或姿态四元数的初值,然后迭代计算摄站位置和姿态四元数的最或然值,直到外方位元素满足精度要求为止。
上述的迭代过程可以描述为下面6个步骤:
(1)读入原始数据,包括内方位元素,像点的观测值及其对应的地面控制点在地面坐标系中的坐标。
(2)确定外方位元素的初值。本文算法为全局收敛算法,给定任意初值均可求解出正确结果。同时按式(8)计算投影矩阵V。
(3)按式(1)计算旋转矩阵M。
(4)按式(12)计算摄站位置 rS(M),并按式(13)计算r′(M)。
(5)对地面点坐标和投影点坐标按式(14)进行重心化,并按式(18)计算矩阵N,通过计算矩阵N的最大特征值所对应的特征向量得到姿态四元数˙q。
(6)重复(3)~(5),直到求解的外方位元素的精度小于给定的限差为止。
3.4 全局收敛的证明
为证明上述迭代算法全局收敛的性质,引入文献[16]中的全局收敛定理及其在文献[11—12]中的证明过程。全局收敛定理可以描述为:
当算法S满足下面三个条件时,则该算法为全局收敛算法:①算法 S为闭算子(其定义在文献[11]中给出);②算法 S所生成的矩阵集{Sk}为有界闭集;③算法S使得总误差函数随迭代次数的增加而减小。
对于本文算法来说,文献[11]中已经证明基于奇异值分解进行绝对定向得到旋转矩阵M的算法是闭映射,而本文采用四元数进行绝对定向得到旋转矩阵M的方法与文献[11]中绝对定向类似,也是闭映射,且计算输入数据为连续数据,因此,本文算法是闭算子,条件①满足。同时本文算法保证了迭代过程中所得到的旋转矩阵M序列为正交矩阵,是有界闭集,条件②满足。对于条件③,设第k次、k+1次迭代后的误差函数分别为 E(M(k))、E(M(k+1)),第 k+1次迭代后的投影向量为则根据式(13),有

利用范数的运算法则,有下面的等式成立[11]

将式(20)代入式(19),得

由于旋转矩阵的求解是使式(14)最小,因此第k+1次求解得到的是使 E(M(k))取得最小的M(k+1),即

将上式代入式(21),可得

上述的证明过程表明,本文提出的基于四元数的空间后方交会算法是全局收敛算法,计算结果与外方位元素初值无关,给定任意的初值均能迭代收敛到正确结果。
4 试验结果与分析
为验证本文提出的基于四元数的空间后方交会全局收敛算法的正确性和有效性,并与惯用的求解方法及文献[8]中算法进行比较,进行了两组试验计算。
第一组试验采用郑州地区的一幅航空影像,其详细参数如表1所示。

表1 实际像片参数Tab.1 The elements of actual image
控制点在影像上均匀分布,其像点坐标由屏幕坐标量测得到,地面坐标由外业测量得到,具体的控制点坐标如表2所示。

表2 实际像片的控制点坐标Tab.2 The control coordinates of actual image

续表2
第二组试验,采用文献[8]中的模拟数据。模拟的外方位元素如表3所示,按严密的共线条件方程模拟了6张像片,具体的坐标数据见文献[8],其中有大航高、大倾角像片,也有小航高、小倾角像片。相机焦距为 100 mm,且 x0=0, y0=0。

表3 模拟像片的外方位元素Tab.3 The exterior orientation elements of simulative images
利用本文算法、传统的迭代方法及文献[8]中的算法分别对郑州地区的实际航片和模拟生成的像片进行空间后方交会计算。由于本文算法是全局收敛算法,迭代初值的计算可以任意给定,试验中取q0= 1,q1=q2=q3=0,即认为像片为水平姿态。传统的迭代解法与文献[8]中算法的初值确定按文献[8]中给定。解算中为便于比较,仍然将姿态四元数转化为欧拉角,解算结果分别如表4、表5所示。

表4 实际像片解算结果Tab.4 The result of calculation for actual image

表5 模拟像片解算结果Tab.5 The result of calculation for simulative images
从表4、表5中的解算结果可以得到看出:
(1)对于实际数据的解算,本文算法解算精度与其他两种方法基本相当,摄站位置最大差值约为0.016 m,摄影姿态最大差值约为0.001°= 3.6″,满足测量要求,表明本文推导的公式正确可靠,新算法可以用于空间后方交会解算。
(2)当姿态角较小,即近似垂直摄影时,本文算法和其他两种方法均能正确求解。
(3)对于各种航高下的大倾角像片,本文算法依然能够正确求解,即算法对各种摄影姿态具有很好的适应性。传统迭代算法不能求解,主要是因为传统迭代算法对共线条件方程线进行线性化时需要良好的初值,当初值不好时,迭代不收敛,不能求解。本文算法无需对共线条件方程进行线性化,是一种非线性方程的迭代方法,对外方位元素初值没有任何要求,并在理论上证明算法的全局收敛性,即对初值的无依赖性,给定任意初值均能正确求解。
(4)从模拟数据解算结果来看,本文算法的求解精度非常高,而对实际数据的解算精度稍低,主要原因是受控制点地面坐标和像点坐标的量测误差影响。因此,从应用的角度来考虑,需要进一步研究全局收敛条件下的抗差空间后方交会和多航带多影像的区域网平差。特别是在区域网平差时,未知数增多,情况变复杂,全局收敛性的确保成关键。事实上本文构造的误差函数在未知数数量增多时,求导后仍然可以变换为式(13)的表达形式,因此可以确保区域网平差时算法的全局收敛性。这也是本文算法的优势所在。
5 结束语
空间后方交会具有十分重要的作用,通过严密的数学推导,提出一种基于四元数的空间后方交会全局收敛算法。该算法主要有两个特点:一是将传统的中心投影共线条件方程用绝对定向和正交投影两种变换公式来代替,同时通过四元数对摄影姿态进行描述,得出非线性方程的直接迭代解算方法,从而无需对传统共线条件方程进行线性化;二是全局收敛算法,即算法可以摆脱传统方法对外方位元素初值的依赖,任意给定初值,都可以求解出正确结果,并从理论上对算法的全局收敛性进行了证明,从而彻底解决了初值问题。当前,随着无人机、无人飞艇等的应用,传感器平台日益增多。由于这些平台因其自身结构的特点或任务的特殊性,很难保证近似垂直摄影条件,如抗震救灾等应急响应时。因此其获取的影像往往不能得到良好的位置和姿态初值,对这些平台获取的大倾角影像进行后方交会将是具有挑战性的工作。本文提出的全局收敛算法可以弥补传统的迭代解法不能进行大倾角后方交会的不足,具有很好的应用潜力。
[1] WANG Zhizhuo.The Principles of Photogrammetry[M]. Beijing:Press of Surveying and Mapping,1990.
[2] J I Qiang,MAURO S C,ROBERT M H,et al.A Robust Linear Least-squares Estimation of Camera Exterior Orientation Using Multiple Geomatric Features[J].ISPRS Journal of Photogrammetry&Remote Sensing.2000,55:75-93.
[3] MENTHON D,DAVIS L S.Exact and Approximate Solutions of the Perspective Three Point Problem[J].IEEE Transactions on PAMI,1992,14(11):1100-1105.
[4] QUAN Long,LAN Zhongdan.Linear N-point Camera Pose Determination[J].IEEE Transactions on PAMI, 1999,21(7):1-7.
[5] LIU M L,WONG K H.Pose Estimation Using Four Corresponding Points[J].Pattern Recogn Lett.1999, 20(1):69-74.
[6] FIORE P D.Efficient Linear Solution of Exterior Orientation[J].IEEE Transactions on PAMI,2001,23(2): 140-148.
[7] ANSAR A,DANIILIDIS K.Linear Pose Estimation from Points or Lines[J].IEEE Transactions on PAMI,2003, 25(5):578-589.
[8] J IANG Gangwu,J IANG Ting,WANG Yong,et al.Space Resection Independent of InitialValue Based on Unit Quaternions[J].Acta Geodaetica et Cartographica Sinica, 2007,36(2):169-175.(江刚武,姜挺,王勇,等.基于单位四元数的无初值依赖空间后方交会[J].测绘学报, 2007,36(2):169-175.)
[9] WANG Yong,J IANG Ting,JIANG Gangwu,et al.Space Resection of Single Image Based on the Description of Unit Quaternions[J].Journal of Zhenzhou Institute of Surveying and Mapping.2007,24(2):133-135.(王勇,姜挺,江刚武,等.基于单位四元数描述的单像空间后方交会[J].测绘科学技术学报,2007,24(2):133-135.)
[10] GUAN Yunlan,CHENG Xiaojun,ZHOU Shijian,et al. A Solution to Space Resection Based on Unit Quaternion [J].Acta Geodaetica et Cartographica Sinica,2008,37 (1):30-35.(官云兰,程效军,周世健,等.基于单位四元数的空间后方交会解算[J],测绘学报,2008,37(1): 30-35.)
[11] LU CHIENPING,HAGER G D,MJOLSNESS E.Fast and Globally ConvergentPose Estimation from Video Images[J].IEEE Transactions on PAMI,2000,22(6): 610-622.
[12] SCHWEIGHOFER G,PINZ A.Fast and Globally Convergent Structure and Motion Estimation forGeneralCamera Models[J].Proc of 17th British Machine Vision Conference.2006:147-156.
[13] HORN K P.A Closed-form Solution of Absolution Orientation Using Unit Quaternion[J].Journal of the Optical Society of America,1987,4(4):629-642.
[14] KEN S.Animating Rotation with Quaternion Curves[J]. Siggraph,1998,19(3):245-254.
[15] HORN K P.Closed-form Solution of Absolution Orientation Using Orthonormal Matrices[J].Journal of the Optical Society of America:Series A,1988,5(7): 1127-1135.
[16] LUENBERGER D G.Linear and Nonlinear Programming [M].3rd ed.Berlin:Springer,2008.

