欠采样率下多频率成分的估计方法

高育兵, 梁红, 杜金香



欠采样率下多频率成分的估计方法

高育兵1, 梁红2, 杜金香2

(1. 海军装备部驻西安地区军事代表局, 陕西 西安, 710054; 2. 西北工业大学 航海学院, 陕西 西安, 710072)

针对信号处理和雷达系统中常见的信号频率大于采样频率或采样频率小于奈奎斯特情况下信号多个频率成分的估计问题, 提出了采用一组非互质的模数和相应的一组有误差的余数, 同时重构多个任意正实数的广义稳健中国剩余定理(GRCRT), 定理1首先给出了余数与重构的正实数的一一对应所需要满足的条件, 定理2 给出了重构正实数有唯一解的条件。将该定理用于欠采样下多个信号频率估计, 仿真实例验证了余数估计有误差时同时估计多个正实数算法的稳健性和实际工程应用前景。

广义稳健中国剩余定理; 欠采样; 多频率估计

0 引言

信号的频率估计在许多工程领域得到广泛的应用。众所周知, 当信号的采样频率大于奈奎斯特采样频率的时候, 可以唯一地确定信号频率, 最简单的就是采用快速傅立叶变换(fast Fourier transform, FFT)方法。但是当信号的采样频率小于奈奎斯特采样频率时, 就不可能从采样样本中唯一地获得信号频率的估计。采样中国剩余定理(Chinese remainder theorem, CRT)可以解决这一问题。近几十年来中国剩余定理在数字信号处理、编码、密码学及计算机等领域获得了广泛的应用[1-3]。传统的CRT利用一组两两互质的模和余数来估计一个整数, 但是只有重构的整数小于这组模的最小公倍数时, 才能唯一确定该整数。文献[4]从相位解卷积的角度出发, 提出了稳健的CRT(robust Chinese remainder theorem, RCRT)重构算法, 但是采用该算法重构的整数局限于与模相关的离散点, 限制了在工程中的应用。文献[5]提出的广义RCRT(generalized RCRT, GRCRT)重构算法, 给出了余数有误差时重构一个任意正整数的方法。文献[6]在文献[5]的基础上给出了余数有误差时重构一个任意实数的方法, 有效地解决了欠采样情况下单个单频信号的频率估计及阵元间距大于半波长时相位解模糊的问题, 但是都没有涉及多个数同时估计的问题。文献[7]虽然给出了多个数同时估计的算法, 但是该方法不能解决所有被估计数的余数都存在误差时如何重构多个数的问题, 这一点限制了它在许多领域的应用。例如, 在数字信号处理中信号中可能包含多个单频成分, 可以采用几次欠采样(欠采样频率对应CRT中模数)获得的样本估计频率(CRT中的一组余数), 如果每次欠采样下频率估计有很小的误差(在低信噪比下), 则如何利用CRT估计多个信号真实频率就成为急需解决的问题。

本文在文献[5]的基础上, 提出了采用一组非互质的模数和相应的有误差的余数同时估计多个任意正实数的广义稳健中国剩余定理, 很好地解决了欠采样频率下多个频率成分信号的估计问题, 仿真算例验证了算法的稳健性及工程实用性。

1 问题的提出

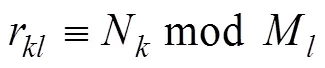
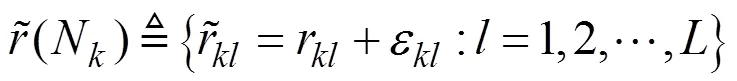
2 同时估计多个正实数的广义稳健中国剩余定理

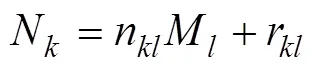
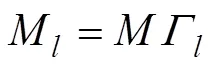
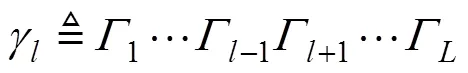
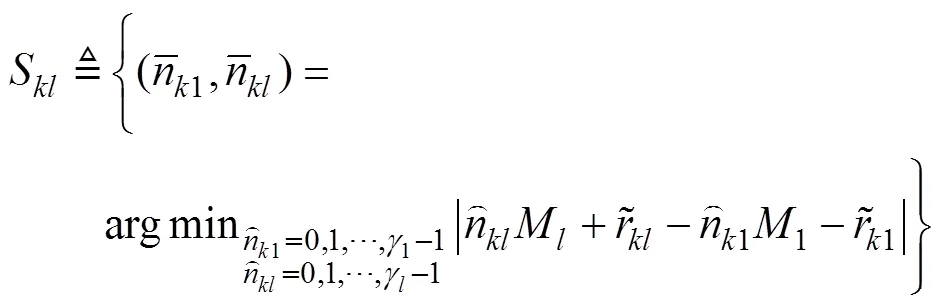
定义

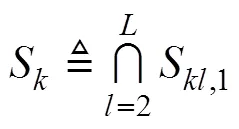
根据上述定义及文献[5]~[7]的启发, 可以得到以下定理。

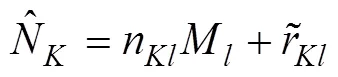
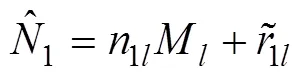
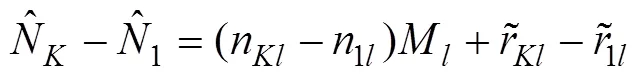
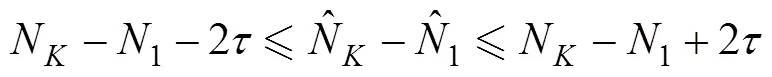
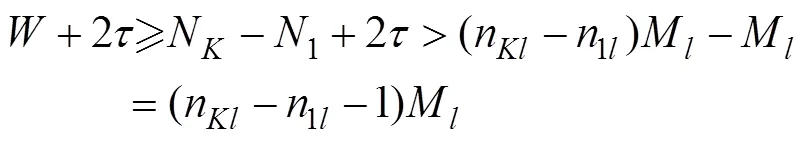
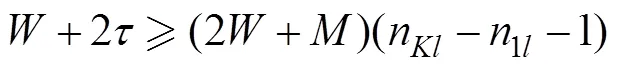
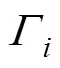
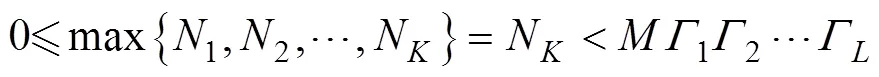
定理2的证明可参见文献[6]。文献[8]和[9]给出了定理2中重构实数的快速算法。

估计的误差上限为

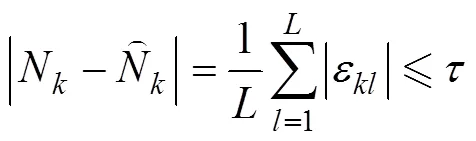
3 欠采样下利用GRCRT估计多个单频信号频率

在实际应用中, 有些情况下获得的样本是不满足Nyquist采样定理要求的, 即欠采样样本。例如信号频率非常高时, 由于实时处理的需要, 采样频率不能太高, 或硬件采样频率达不到要求。此时如果利用欠采样的样本进行信号的参数估计就不能获得准确的估值。如果需要估计的频率成分只有1个, 文献[6]给出了重构单个实数的方法。而信号处理中很多情况下信号包含的频率成分较多, 此时可以采用本文提出的同时估计多个正数的GRCRT 算法, 对欠采样下多个频率成分进行估计。文中对含有2个单频成分的信号频率进行估计, 并给出仿真结果。

仿真中复信号为

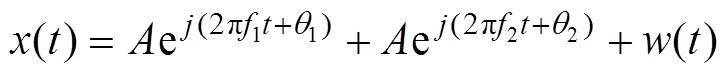
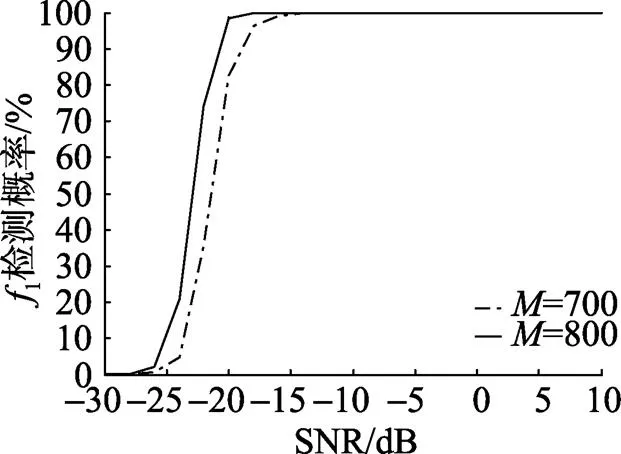
图1 M变化信号频率为f1时信噪比与检测概率之间的关系曲线

图2 M变化信号频率为f2时信噪比与检测概率之间的关系曲线

图3 M变化信号频率为f1时信噪比与估计的均方误差之间的关系曲线

4 结束语

本文提出了解余数有误差时同时估计多个正实数的广义稳健中国剩余定理, 得出算法估计的误差仅与余数估计的误差有关, 克服了传统CRT算法极小的余数误差带来相当大整数估计误差的局限。用信号处理中的仿真实验验证了所提GRCRT算法的有效性和稳健性。算法适用于估计的所有余数有误差时重构多个正实数的场合, 可以应用于数字信号处理中的雷达、声纳及生物医学等领域。

[1] Krishna B, Krishna H C, Lin K Y. Computational Number Theory and Digital Signal Processing: Fast Algorithms and Error Control Techniques[M]. CRC Press, Boca Raton, FL, USA, 1994: 1-5.

[2] Grossschadl J. The Chinese Remainder Theorem and its App- lication in a High-speed RSA Crypto Chip[C]//16th Annual Conference on Computer Security Applications, New Orleans, USA, 2000: 384-393.

[3] Ding C, Pei D, Salomaa A. Chinese Remainder Theorem: Applications in Computing, Coding, Cryptography[M]. Sin- gapore: World Scientific, 1996: 2-10.

[4] Xia X G , Wang G. Phase Unwrapping and A Robust Chinese Remainder heorem[J]. IEEE Signal Processing Letters, 2007, 14(4): 247-250.

[5] Li X W, Liang H, Xia X G. A Robust Chinese Remainder Theorem with its Applications in Frequency Estimation from Undersampled Waveforms[J]. IEEE Transactions on Signal Processing, 2009, 57(11): 4314-4322.

[6] 梁红, 张琦. 广义稳健的中国剩余定理及其在欠采样率下频率估计中的应用[J]. 电子与信息学报, 2010, 32(8): 1802-1805. Liang Hong, Zhang Qi.A Generalized Robust Chinese Re- mainder Theorem and Its Application to Frequency Esti- mation with Undersampling[J]. Journal of Electronics & In- formation Technology, 2010, 32(8): 1802-1805.

[7] Zhou G C, Xia X G. Multiple Frequency Detection in Un- dersampled Complex-valued Waveforms with Close Multiple Frequencies[J]. Electronics Letters, 1997, 33(15): 1294-1295.

[8] Li G, Xu J, Peng Y N, et al. An Efficient Implementation of Robust Phase Unwrapping Algorithm[J], IEEE Signal Proce- ssing Letters, 2007, 14(6): 393-396.

[9] Li X, Xia X G. A Fast Robust Chinese Remainder Theorem Based Phased Unwrapping Algorithm[J]. IEEE Signal Proce- ssing Letters, 2008, 15(10): 665-668.

Multiple-Frequency Estimation Method with Undersampled Waveform

GAO Yu-bing1, LIANG Hong2, DU Jin-xiang2

(1. XI′an Representative Bureau, Naval Armament Department, Xi′an 710054, China; 2. College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)

In some applications, such as signal processing and radar systems, it is preferred that the range of the frequencies is as large as possible for a given sampling rate and the sampling rate is below the Nyquist rate. In both cases, frequencies estimation from undersampled waveforms is necessary. In this paper, a generalized robust Chinese remainder theorem (GRCRT) for reconstructing multiple positive real numbers is presented, where modules are not pair-wisely co-prime and the remainders with errors. In theorem 1, the sufficient condition for the multiple real numbers to satisfy is given, where all remainders have errors and we can determine which one in the remainder set is the remainder of any real number. And an approach to determine unique solution of multiple real numbers from the remainder set with errors is proposed in theorem 2. Simulation results show that the present method is efficient for estimating multiple frequencies from multiple undersampled waveforms with sampling rate below the Nyquist rate, and it can be applied to such areas as digital signal processing.

generalized robust Chinese remainder theorem(GRCRT); undersample; multiple-frequency estimation

TJ630.34；TN911.7

A

1673-1948(2012)01-0019-05

2011-04-11;

2011-06-10.

国家自然科学基金(60702067).

高育兵(1964-), 男, 高级工程师, 研究方向为水声信号处理.

(责任编辑: 杨力军)