含非线性项的2D时变系统迭代学习控制

梅中伟， 朱芳来

(同济大学电子与信息工程学院，上海 201804)

0 引言

对于一个具有重复运行性质的系统，迭代学习能够通过改变控制输入使系统的输出轨迹渐近地跟踪给定的期望轨迹。迭代学习不需要知道系统参数，适合于那些难以建模和对轨迹控制精度要求非常高的系统。传统的迭代学习［1－3］的一个缺点是难以找到一个同时描述控制系统在时域上的动态特性和在迭代方向上的学习率的数学模型。2D(Two Dimensional)系统包含两个动态过程，表征系统在水平和垂直方向上的动态变化，而迭代学习同样包含了两个过程，时间过程上的动态特性和迭代过程，因此可以将2D系统理论和迭代学习很好地结合在一起。

近年，许多学者在原有的基于2D系统理论的迭代学习控制［4］基础上进行了更为深入的研究。文献［5］研究了含可变初始条件的离散系统的迭代学习;文献［6］将2D系统理论应用于线性离散系统，给出了一种经一次迭代输出误差即收敛至零的控制方法;文献［7］针对一类含输入时滞的非线性离散系统提出了一种迭代算法，使得系统能在不确定初始状态下跟踪误差收敛到零;文献［8］利用2D系统理论讨论了开闭环迭代学习控制并给出了系统收敛的充分必要条件;文献［9］提出了一种基于Roesser模型的MIMO系统学习率的参数选取方法，并给出了受扰动的线性时变离散系统输出收敛的充分条件;文献［10］通过引入以往控制信息对当前控制的影响函数，构造了一个具有较快收敛速度的新型迭代学习算法并利用2D理论证明了其收敛性;文献［11］在文献［6］的基础上将2D线性时变离散系统的ILC过程转变为1D线性时不变离散系统的ILC过程，并给出了两类特殊的线性时变离散系统收敛的充分和必要条件。

本文针对含有非线性项的时变系统，提出了一种基于Roesser模型的2D学习率，与传统的非线性系统差分型迭代学习率进行了比较，证明改进后的学习率具有更快的收敛速度。最后，对一个实际系统进行了数值仿真，并与差分型算法进行比较，验证了文中所提方法的正确性。

1 Roesser模型及其收敛条件

2D时变系统的Roesser模型可由式(1)定义

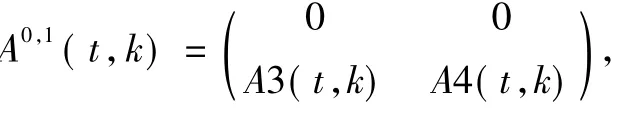
2 含非线性项的时变离散系统的ILC学习律

考虑如下含非线性项的时变离散系统

式中:x(t)∈Rn，u(t)∈Rm，y(t)∈Rp分别为系统的状态向量，输入向量和输出向量;f(x，t)为非线性项，是关于状态向量x(t)和时间t的非线性函数，并且满足Lipschitz条件;A(t)，B(t)，C(t)为具有适当维度的实矩阵。设式(2)满足如下几个假设。

假设1 非线性项f(x，t)满足全局Lipschitz条件，即对任意的 t∈［0，T］存在常数 kf，使得‖f(x1，t) －f(x2，t)‖≤kf‖x1－ x2‖。

假设2 每次迭代的初始条件总是相同的，即xk(0)=xd(0)。其中:xk(0)表示第k次的初始状态;xd(0)表示期望轨迹的初始状态。

假设3 矩阵C(t)B(t－1)满秩。

迭代学习控制可以做如下描述:对于给定的式(2)，在满足边界条件x(0)=x0的前提下，寻找一个理想控制输入u(t)，t=0，1，…，N －1，使得系统能够完全跟踪期望输出轨迹 yr(t)，t=0，1，…，N。下面给出一种通用的ILC学习律

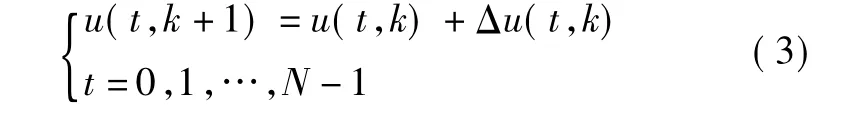
式中，Δu(t，k)是对第k次控制输入的修正量。将式(2)写成2D Roesser模型

边界条件为

记迭代学习的第k次和第k+1次状态值之差为η(t，k)=x(t－1，k+1) －x(t－1，k)，非线性项之差为Δf(t，k)=f(x(t－1，k+1)，t－1) － f(x(t－1，k)，t－1)，输出误差为 e(t，k)=yr(t) － y(t，k)。由式(4)和式(5)可知

结合式(6)和式(7)

令

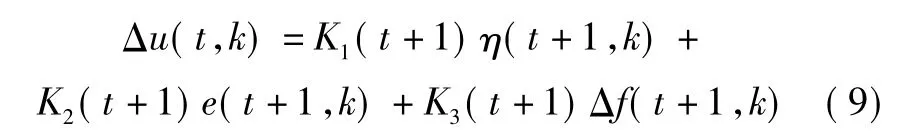
将式(9)代入式(8)中，可得

为了将式(10)转变为标准的2D Roesser模型，取

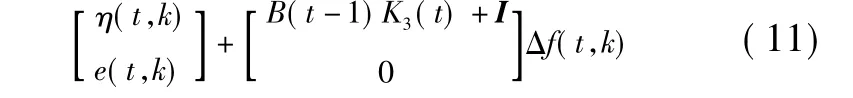
由于非线性项满足 Lipschitz条件 Δf(t，k)≤K·，即Δf(t，k)存在一定的上限 ε，故一定存在这样的离散函数K4(t)和K5(t)使得Δf(t，k)=K4(t)·η(t，k)+K5(t)e(t，k)。将 Δf(t，k)代入到式(11)中，整理得

其中

假设R(t)=

由于第k+1次系统的状态未知，所以无法直接使用上述学习率。在算法中使用开环差分型迭代学习率［12］对第k+1次的状态进行估计。

基于以上推论给出下面的校正算法。

1) 当 k=0 时，u0(t)=0，x(0)=x0，并取 K(t，k)=β(t，k)(C(t)B(t－ 1))T［C(t)B(t－ 1)(C(t)B(t－1))T］－1，K2(t)=(C(t)B(t－1))T［C(t)B(t－1)(C(t)·B(t－1))T］－1，K1(t)= － K2(t)C(t)A(t－1)，K3(t)=－ (C(t)B(t－1))T［C(t)B(t－1)(C(t)B(t－1))T］－1·C(t)，其中 β(t，k)为一个待定参数使得 K(t，k)满足‖I－K(t，k)C(t+1)B(t)‖≤p＜1，设置最大迭代次数为 Kmax。

2) 如果 k＜Kmax或者

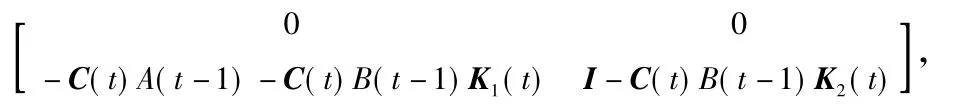
则从引理1可以得到如下定理。

定理1对于含有非线性项的线性离散系统，若存在矩阵 K1(t)和 K2(t)使得‖R(t)‖＜1，t=1，2，…，则迭代学习控制率1，2，…，N，设置 Fflag=0，否则设置 Fflag=1。根据步骤1)计算 y(t，0)，并用开环迭代学习率计算 u(t，1)的预估值 uα(t，1)，即 uα(t，1)=u(t，0)+K(t+1)·(e(t+1，0) －e(t，0))。从而将 uα(t，1)代入式(2)可得系统的状态值 xα(t，1)以及 y(t，1)的估计值 yα(t，1)。

3)根据 yα(t，1)，得出第一次的误差估计值eα(t，1)。将 eα(t，1)、xα(t，1) 分别当作 e(t，1) 和x(t，1)，从而可以使用学习率 u(t，k+1)=u(t，k)+K1(t+1)［x(t，k+1) － x(t，k)］+K2(t+1)e(t+1，k)+K3(t+1)［f(x(t，k+1)，t) － f(x(t，k)，t)］得出校正后的 y(t，1)。

校正算法流程如图1所示。

图1 校正算法结构流程图Fig.1 The flow chart of the correction algorithm

3 数值仿真

本文所用的仿真示例来源于文献［6］，在原系统的基础上加入了非线性项

对于此仿真实例，取初始条件 x(0)=0，K(t，k)的值取为 K(t，k)=0.5(C(t)B(t－1))T［C(t)B(t－1)·(C(t)B(t－1))T］－1，期望轨迹为 yd(t)=1.5 sin(0.06t)，t=0，1，2，…，N。仿真结果如图2 ～图4 所示。

从图2可以看到系统在式(14)的作用下，输出曲线逐渐逼近于给定的期望曲线;图3显示了最后一次迭代的时候系统的输出曲线已经完全和给定的期望轨迹重合;图4所示为差分型ILC学习率和校正算法收敛速度的比较，从图中可以看出改进后的算法具有更快的收敛速度，并且跟踪性能良好。

图2 系统在式(14)作用下每次迭代产生的输出曲线和期望输出曲线Fig.2 Tracking performance of ILC system output at different time－steps and iterations using ILC rule(14)

图3 最后一次迭代的输出曲线和期望输出曲线Fig.3 Tracking performance of ILC system output at the last iteration

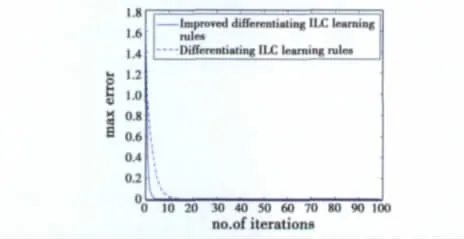
图4 差分型ILC学习率和校正算法收敛速度比较Fig.4 The total squared error at different numbers of iterations using the proposed ILC rule(14)and discrete differentiating ILC rules

4 结论

本文基于2D系统理论，对含非线性项的时变离散系统提出了一种改进的学习率，将2D系统理论引入非线性系统的迭代学习控制，拓宽了2D系统理论应用于迭代学习控制的范畴。与传统的非线性系统的迭代学习率相比，本文提出的学习率可以有效地提高迭代学习的收敛速度，在经过有限次的迭代后能使系统输出完全跟踪给定的输出曲线。

［1］ LONGMAN R W.Iterative learning control and repetitive control for engineering practice［J］.International Journal of Control，2000，73(10):930－954.

［2］ 皮道映，孙优贤.非线性时变系统开闭环P型迭代学习控制的收敛性［J］.自动化学报，1999，25(3):351－354.

［3］ 蒋思中，朱芳来，王心开，等.模糊增益PD型迭代学习算法及其应用［J］.电光与控制，2009，16(8):72－74.

［4］ KUREK J E，ZAREMBA M B.Iterative learning control synthesis based on 2－D system theory［J］.J of Intell Robot Syst.1993，38(1):121－125.

［5］ FANG Y，CHOW T W S.2－D analysis for iterative learning control for discrete－time systems with variable initial conditions［J］.IEEE Transactions on Circuits and Systems－I:Fundamental Theory and Applications，2003，50(5):722－727.

［6］ LI X D，HO J K L，CHOW T W S.Iterative learning control for linear time－variant discrete systems based on 2－D system theory［J］.IEE Proc:Control Theory and Applications，2005，152(1):13－18.

［7］ LI X D，CHOW T W S，HO J K L.Iterative learning control for a class of nonlinear discrete－time systems with multiple input delays［J］.International Journal of Systems Science，2008，39(4):361－369.

［8］ 蒋思中，王改云.基于2－D系统理论的D型开闭环迭代学习控制［J］.电光与控制，2010，17(1):37－39.

［9］ 黄彧伟，张国山.受扰动2－D线性时变系统的迭代学习控制［J］.控制理论与应用，2007，24(6):999－1003.

［10］ 林辉，回立川.基于影响函数的迭代控制器2－D分析与设计［J］.信息与控制，2009，38(5):558－562.

［11］ LI X D，HO J K L.Further results on iterative learning control with convergence conditions for linear timevariant discrete systems［J］.International Journal of Systems Science，2011，42(6):989－996.

［12］ SAAB S S.Robustness and convergence rate of a discrete－time learning control algorithm for a class of nonlinear systems［J］.International Journal of Robust Nonlinear Control，1999，9(9):559－571.