一道课本习题的解法探究及应用

●

(深圳市高级中学 广东深圳 518040)

一道课本习题的解法探究及应用

●黄元华

(深圳市高级中学 广东深圳 518040)

本文研究一道关于直线与圆位置关系的课本习题(苏教版高中数学必修2第118页第26题).同类题目在各种高中数学考试试题与教辅资料中频繁出现，但不少高中阶段的学生对此类题目望而生畏，故有必要对其解法加以深入研究.该题的解法较多，本文就不一一呈现，只提供2种比较特殊的解法，并拓展应用到解决一般的圆锥曲线问题中.

1 原题呈现

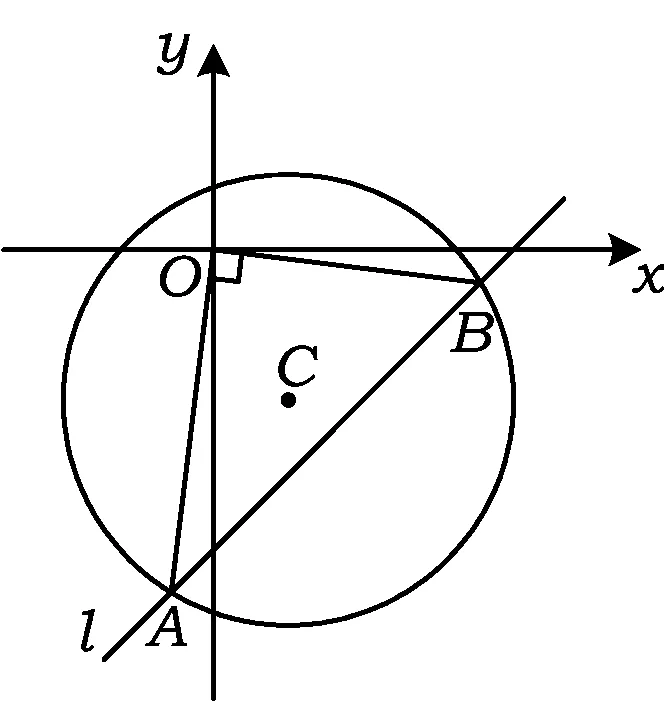
图1

题目如图1所示，已知圆C:x2+y2-2x+4y-4=0，是否存在斜率为1的直线l,使以l被圆C截得的弦AB为直径的圆过原点?若存在,求出直线l的方程；若不存在,说明理由.

2 解法探究

解法1设A(x1,y1),B(x2,y2).假设该圆过原点O，则OA⊥OB，从而

kOA·kOB=-1，

即

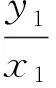
设所求直线l的方程为y=x+m，即

圆C方程为x2+y2-2x+4y-4=0，即

将式(1)代入式(2)，得

(m2+2m-4)x2+(m2+4m-4)y2+(8-6m)xy=0，

变形为

由韦达定理得

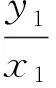
解得

m=1或m=-4，

故所求直线方程为y=x+1或y=x-4.

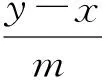
解法2设A(x1,y1),B(x2,y2).联立直线l与圆C的方程,分别消去y,x,得

式(3)+式(4),得

2x2+2y2+2(m+1)x+2(1-m)y+2m2+6m-8=0.

因为该圆过原点O(0，0),所以

m2+3m-4=0，

解得

m=1或m=-4,

故所求直线方程为y=x+1或y=x-4.

评注此法构思巧妙，它提供了一种求以直线和圆锥曲线的相交弦为直径的圆的方程的方法,即将直线方程与曲线方程联立,分别消去x，y,得到关于y，x的2个一元二次方程,然后2式迭加,即得所求圆的方程.其原理何在？简述如下：

若圆的一直径的2个端点分别为A(x1,y1)，B(x2,y2),则圆的方程为

(x-x1)(x-x2)+(y-y1)(y-y2)=0,

变形即为

x2-(x1+x2)x+x1x2+y2-(y1+y2)y+y1y2=0.

该式可看作是

x2-(x1+x2)x+x1x2=0

与

y2-(y1+y2)y+y1y2=0

迭加而成，且一次项和常数项明显呈现出韦达定理的特征．据此可知，对于某些直线与圆锥曲线相交的问题，可将直线方程代入曲线方程，分别得出关于x及y的一元二次方程，然后2式迭加即得以直线与曲线相交弦为直径的圆的方程．

3 拓展应用

下面用解法1和解法2各解决2个相关的圆锥曲线问题.

图2

例1如图2所示，已知直线y=x+b与抛物线x2=2y交于点A,B,且OA⊥OB(O为坐标原点),求b的值.

解设A(x1,y1),B(x2,y2).直线l的方程y=x+b,即

抛物线方程为x2=2y·1,

(6)

将式(5)代入式(6),得

整理得

2y2-2xy-bx2=0,

即

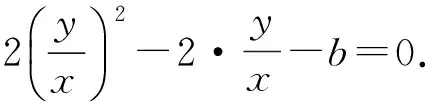
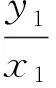
从而

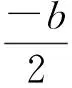
解得

b=2．

例2如图3所示，已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1.

图3

(1)求椭圆C的标准方程.

(2)若直线l：y=kx+m与椭圆C相交于点A,B(A,B不是左、右顶点),且以AB为直径的圆过椭圆C的右顶点.求证:直线l过定点,并求出该定点的坐标.

(2007年山东省数学高考理科试题)

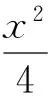
(2)借助几何画板演示，观察得知直线l过定点.由题意知椭圆右顶点为P(2,0)，设A(x1,y1),B(x2,y2)，则

y=k(x-2)+2k+m.

若2k+m=0,则l过定点(2,0),这与已知矛盾,故2k+m≠0,直线方程可变形为

(7)

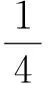
即 3(x-2)2+12(x-2)·1+4y2=0.

(8)

将式(7)代入式(8),得

整理得

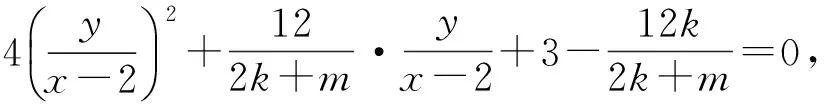
解得

例3求经过2个圆：x2+y2+6x-4=0和x2+y2+6y-28=0的交点且面积最小的圆的方程．

解易知所求圆为以2个已知圆公共弦为直径的圆．2个圆方程为

式(9)-式(10)，得公共弦所在的直线方程为

由式(9)，式(11)分别消去y,x得

x2+7x+6=0,y2-y-6=0，

2式迭加得

x2+y2+7x-y=0,

图4

即为所求圆的方程.

解设椭圆的方程为ax2+by2=1(a>0,b>0,a≠b).由y=x+1及ax2+by2=1分别消去y，x得

式(12)，式(13)相加，得以PQ为直径的圆的方程为

(a+b)x2+(a+b)y2+2bx-2ay+a+b-2=0.

(14)

由于OP⊥OQ,故该圆过原点(0，0),即a+b=2，代入式(14)，得

x2+y2+bx-ay=0,

即

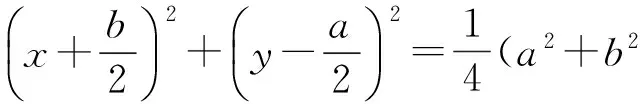
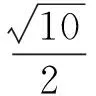
即

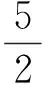
又由a+b=2，可解得

故所求的椭圆方程为

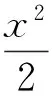
课本和各种教学参考书为我们提供了大量的有价值的典型题目，这些题目具有入口宽、解法多、综合性强、考查面广的特点，其解法往往可以拓展应用到其他题型中去.这些典型题目备受各类考试命题者的青睐，成为各类考试的“题源”.因此，有必要经常对这些典型题目的解法加以拓展探究.只要坚持下去，必将收到举一反三、以少驭多的效果.

[1] 李爱生.教材原题多解探究[J].考试(高考·试题设计)，2011(5):16-19.

浙江省初、高中数学新课程“疑难问题解决”专题研讨会分别在嘉兴、余姚举行

2011年浙江省初、高中数学新课程“疑难问题解决”专题研讨会于11月下旬分别在嘉兴实验初中和余姚中学顺利举行。本次活动由浙江省教育厅教研室、浙江省数学会主办，浙江省各地市初、高中数学教研员、数学骨干教师500余人参加了此次活动。浙江师范大学期刊社副社长、《中学教研》(数学)主编张翼教授出席了此次会议，加强了我刊与中学数学界的联系与交流。本次会议的主题是初、高中数学课堂教学目标的有效设计与落实及其疑难问题的解决。旨在帮助一线教师进一步提升解决课程改革中疑难问题的能力，推动初、高中数学新课程的深入实施。会议形式丰富，安排紧凑，内容充实，实实在在地解决了一线教师在课程改革中遇到的一些疑难问题，使参与培训的教师开阔了眼界、收获了智慧，促进了教师的教学实践与研究，并将有效地推动我省初、高中数学教学水平的提升。