三个立方幂等矩阵的线性组合的相关性质
张绪绪
(陕西工业职业技术学院 基础部, 陕西 咸阳 712000)
0 引言
幂等矩阵在矩阵理论和统计学中具有重要的应用,诸如文献[1,2].近几年立方幂等矩阵线性组合的相关性质也引起了许多学者的重视和研究,并得到了相应的结论.文献[3]给出了两个可交换的立方幂等矩阵的线性组合是立方幂等矩阵的充分必要条件,本文在文献[4-10]研究结果的基础上,通过向量空间向量组的秩,研究了三个非零的两两可交换的n×n立方幂等矩阵P1,P2,P3的线性组合是立方幂等矩阵的等价条件.
1 预备知识
定义1[4]任意矩阵A∈Cn×n,如果A3=A,则A称是立方幂等矩阵.
定义2[5]矩阵A,B∈Cn×n,如果AB=BA,则称矩阵AB是可交换的.
2 重要结论
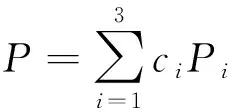
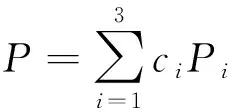
(1)c1+c2+c3=±1;
(2)c1+c2-c3=±1;
(3)c1-c2+c3=±1;
(4)c1-c2-c3=±1.
证明:必要性显然.下证充分性.
因为P2=aP1,P3=bP1,a,b∈C,所以a=±1,b=±1,
c1P1+c2aP1+c3bP1=(c1+c2a+c3b)P1
又因为P3=P,P13=P1,故
(c1+ac2+bc3)3P13=(c1+ac2+bc3)P1,
(c1+ac2+bc3)3=(c1+ac2+bc3)
则c1+ac2+bc3=±1.
若(ab)=(1 1),则c1+c2+c3=±1;
若(ab)=(1 -1),则c1+c2-c3=±1;
若(ab)=(-1 1),则c1-c2+c3=±1;
若(ab)=(-1 -1),则c1-c2-c3=±1.证毕.
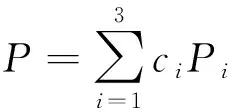
(1)若P1是向量组{P1,P2,P3}的极大线性无关组,即P2=aP1,P3=bP1,a,b∈C,则P3=P当且仅当
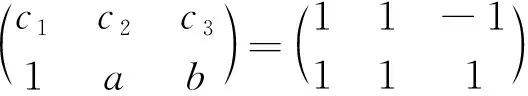

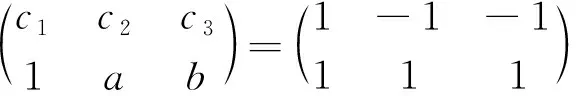
(2)若P2是向量组{P1,P2,P3}的极大线性无关组,即P1=aP2,P3=bP2,a,b∈C,则P3=P当且仅当
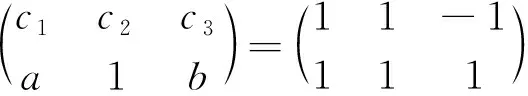


(3)若P3是向量组{P1,P2,P3}的极大线性无关组,即P1=aP3,P2=bP3,a,b∈C,则P3=P当且仅当
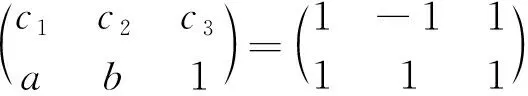


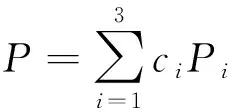
(1)c1+c3a=1,c2+c3b=-1或c1+c3a=-1,c2+c3b=1,其中P12P2=P1P22.
(2)c1+c3a=1,c2+c3b=-2或c1+c3a=-1,c2+c3b=2,其中P12P2=P2=P1P22.
(3)c1+c3a=2,c2+c3b=-1或c1+c3a=2,c2+c3b=1,其中P12P2=P1=P1P22.
(4)c1+c3a=1,c2+c3b=1或c1+c3a=-1,c2+c3b=-1,其中P12P2=-P1P22.
(5)c1+c3a=1,c2+c3b=2或c1+c3a=-1,c2+c3b=-2,其中P12P2=P2=-P1P22.
(6)c1+c3a=2,c2+c3b=1或c1+c3a=-2,c2+c3b=-1,其中P12P2=-P1=-P1P22.
证明:因为P3=aP1+bP2,则
由文献[6]推论2可知上述定理成立.
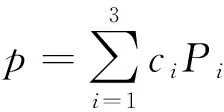

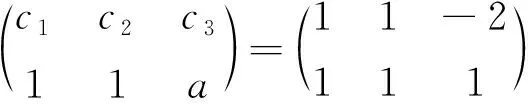
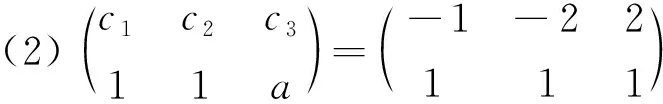
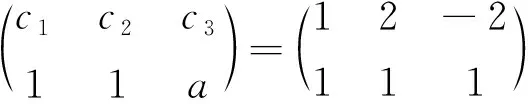

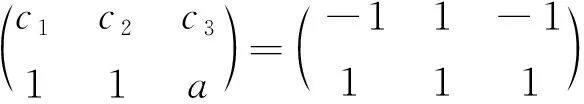

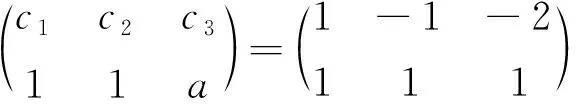
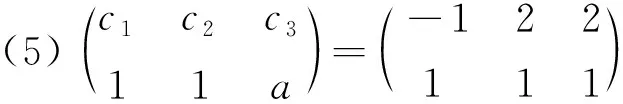



此处对于{P1P3},{P2P3}分别是向量组{P1P2P3}的极大线性无关组的情况不做讨论.
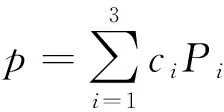




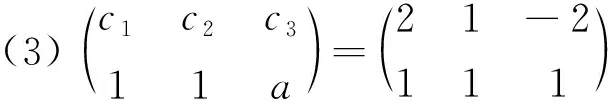





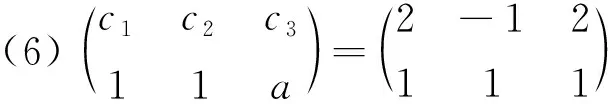
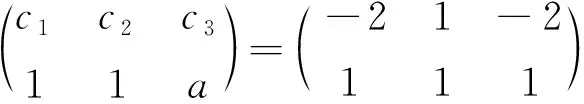
此处对于{P1P3},{P2P3}分别是向量组{P1,P2,P3}的极大线性无关组的情况也不做讨论.
以上推论是定理2 的特殊情况,故均可有定理2得出,在这里就不作证明.
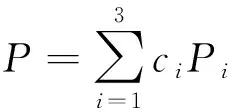
证明:(1)必要性
因为矩阵P是立方幂等矩阵,所以
P3=(c1P1+c2P2+c3P3)3
=c1P+c2P+c3P
(1)
又PiPj=PjPi,P1P2P3=0,所以(1)等价于
(2)
由Pi2Pj=PiPj2(i≠j,i,j=1,2,3)可得
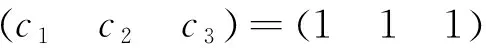
(2)充分性
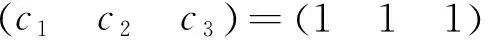
6P1P2P3,
当PiPj=PjPi,P1P2P3=0时,P3=P1+P2+P3=P.同理可证(2)的充分性.
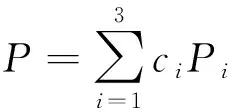


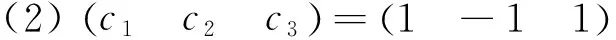

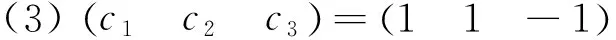

-P1P22,P12P3=P1P32,P22P3=-P2P32.





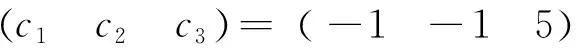
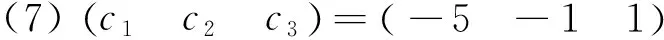

-P12P2,P12P3=P1=P1P32,P22P3=-P2P32.
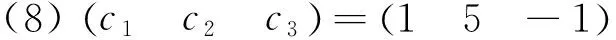
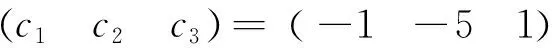
-P1P22,P22P3=P2=P2P32,P12P3=P1P32.


证明:由(2)减(2)×P12得
(3)
由(2)减(2)×P22得
(4)
由(2)减(2)×P32得
(5)
(Ⅰ)当P22P3=-P2P32时,(3)式成立的条件是c2=c3=1或c2=c3=-1.把c2=c3=1代入(2)式得
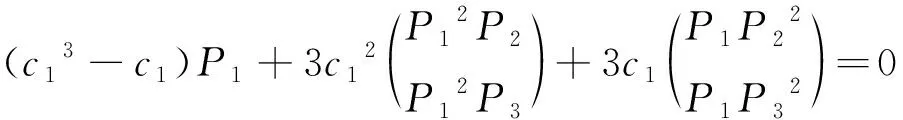
该式成立的充要条件是c1=-1,c2=c3=1且P12P2=P1P22,P12P3=P1P32.同理,c2=c3=-1把代入可得(2)式成立的充要条件是c1=1,c2=c3=-1, 且P12P2=P1P22,P12P3=P1P32.
于是结论(1)成立,同理可证结论(2)、(3)成立.
(Ⅱ)若P12P2=P1P22,P12P3=P1P32,c1≠±1,则(4)式和(5)式可化为:
(c33-c3)(P3-P12P3)=0和(c23-c2)(P2-P22P3)=0,所以c3=1或c3=-1,c2=1或c2=-1.把c3=1,c2=1代入(2)式可得
所以结论(4)成立,同理可证结论(5) (6)成立.
(Ⅲ)若P1P22=P1=-P12P2,P12P3=P1=P1P32,c1≠±1,且(4)式和(5)式可化为(c33-c3)(P3-P12P3)=0和(c23-c2)(P2-P22P3)=0,所以c3=1或c3=-1,c2=1或c2=-1,把c3=1,c2=-1代入(2)式可得
于是结论(7)成立,同理可证结论(8)、(9)成立.
[1] J.K.Baksalary,O.M.Baksalary,Styan GPH.Idempotency of linear combination of an idempotent matrices and a tripotent matrix[J].Linear Algebra Appl,2002,354:21-34.
[2] Puh.K,Yao X Y,Deng C Y.Invertibility of linear combination of two idempotent matrices[J].Proceeding of the American Mathematical Society,2005,133:1 451-1 457.
[3] J.K. Baksalary,O.M.Baksalary.Idempotency of linear combination of two idempotent matrices[J].Linear Algebra Appl,2004,388:45-51.
[4] 王秀芳.幂等矩阵性质的研究[J].连云港师范高等专科学校学报,2007,21(3):84.
[5] 杨凯凡.三次幂等矩阵的线性组合的三次幂等性[J].喀什师范学院学报,2009,30(3):9-12.
[6] 卜长江,李 娜.矩阵线性组合幂等性及立方幂等性的一些结论[J].哈尔滨工程大学学报,2009,30(12):1 458-1 460.
[7] 曹重光.线性代数[M].呼和浩特:内蒙古出版社,1999.
[8] 杨克勋,包学游.矩阵分析[M].哈尔滨:哈尔滨工业大学出版社,1988.
[9] 戴 华.矩阵轮[M].北京:北京科技出版社,2001.
[10] 陈大新.矩阵理论[M].上海:上海交通大学出版社,1991.

