数字平均对红外单光子探测器中温度控制系统信噪改善比的影响*

王进 魏正军 王赓 郭莉 王金东 张智明 郭健平 郭邦红 刘颂豪

(华南师范大学，广东省微纳光子功能材料与器件重点实验室，量子信息技术广东高校重点实验室，广州 510006)

(2012年5月30日收到;2012年7月24日收到修改稿)

1 引言

单光子探测技术是量子信息科学研究与应用中的关键技术，同时在各种微弱信号测量领域有着广泛的应用.随着量子信息技术的兴起，对于红外单光子探测器的需求越来越旺盛.目前，利用InGaAs雪崩光电二极管(APD)进行单光子探测仍是应用的主流方案.通过不断的方案创新和技术改良，在探测速度方面，采用正弦门控方案的单光子探测器工作频率可以达到1.5 GHz[1]，自差分方案实现了2 GHz的工作频率[2];在探测效率方面，积分门控方案把商用APD的探测效率提高到了29.9%[3,4]，一种改进的自差分方案将探测效率提高到30.5%[5];在暗计数率方面，APD平衡相消方案[6]将暗计数率降低到了7×10-7每门，正弦门控方案[1]的暗计数率可以降到6.3×10-7每门.

但是，作为一种准确可靠的测量仪器，精密控制雪崩光电二极管工作点的驱动技术仍需要发展.工作温度对于APD的工作特性有很大的影响：由热激发暗电流引起的暗计数率随温度的降低而降低，但是，由后脉冲引起的暗计数率随温度的降低而升高[7].更重要的是温度变化导致APD的雪崩击穿电压发生变化.APD的偏置电压与雪崩击穿电压的差值被称为过偏压，这是决定APD工作特性的主要参数.在偏置电压、甄别器门限电平等其他工作条件一定的情况下，温度越低，雪崩击穿电压越低，过偏压越大，探测器的探测效率越高，但是暗计数率也急剧上升.因此，温度的变化将导致单光子探测器的暗计数率、后脉冲率和探测效率的变化，从而影响测量结果的可靠性，并可能给量子保密通信系统带来安全隐患[8].由于APD的输出信号是一个复杂的随机分布，难以提取出有效的反馈信号，不能形成一个能够稳定工作点的反馈环路.因此，只能采用工作参数绝对稳定的方式.而工作在雪崩击穿电压之上的APD对温度和偏置电压非常敏感，这就对APD的伺服系统的精度提出了很高的要求.

相对于液氮制冷，半导体制冷器因其具有结构紧凑、体积小、重量轻、控温方便等优势，成为APD制冷器的首选.半导体制冷器配合采用比例-微分-积分(PID)算法的闭环控制器可以实现很高的控温精度.而温度控制的首要条件就是温度值的准确测量.当探测很微小的温度变化时，得到的物理量非常微弱，对噪声的处理变得非常重要，这是微弱信号探测应用领域的一个共性问题.在国防军事、工业、医疗等领域中存在大量微弱信号检测的问题.微弱信号不仅是指信号的幅度很小，而且信号被淹没在噪声中，微弱是相对于噪声而言的.在微弱信号探测以及信号的处理过程中，我们都需要抑制或消除噪声，提高系统的信噪比.目前，微弱信号检测方法和技术主要有锁定放大、取样积分、相关检测[9,10]、自适应噪声抵消和数字平均[11,12]等检测方法，同时小波变换[13-15]、混沌理论[16,17]等微弱信号的检测新方法也获得工程应用.

在温度探测与控制系统中，通常采用数字平均对噪声进行抑制.数字平均技术利用信号进行多次采样并累加平均后，信号幅值得到增强，而随机性的干扰噪声在一定程度上会相互抵消来改善系统的信噪比.这一方案广泛应用于低频微弱信号的噪声处理[18,19].

很多工程性√的论文对于数字平均得到的信噪改善比都采用(N为平均次数)的计算方法[20].西安交通大学王凤坤等[21]在测量液体表面张力系统中，为了提高系统信噪比采用了数字平均技术，并通过实验确定了最佳采样时间和平均次数，但是没有给出定量的理论计算.我们在实验中发现，数字平均方法得到的系统信噪改善比与很多参数有关，不是简单的本文具体研究了采样周期、平均次数、总采样时间对系统信噪比的影响，并说明这些参量对实际应用中的指导意义.

2 温度探测与控制系统中噪声以及数字平均对信噪改善比的影响

2.1 温度探测与控制系统的主要噪声类型

白噪声是电子器件和电路中最常见的一种噪声，电阻的热噪声、PN结的散弹噪声都是白噪声.白噪声的功率谱密度函数为常数，各种频率成分的强度相等.

实际温度控制系统的噪声主要为电阻热噪声和PN结的散弹噪声.热噪声是由于电阻中大量电子的随机热运动引起的，这种大量的随机事件导致的现象必然具有高斯分布的概率密度函数;散弹噪声是由于电子或空穴的随机发射导致流过势垒的电流在其平均值附近随机起伏，也是大量独立随机事件综合的结果，其幅度分布为高斯分布[23].因此，这两种噪声都属于高斯白噪声，在仿真计算时，可以用高斯分布来进行计算.

温度的变化相对于电子线路来说，是一个非常缓慢的过程，通常采用低通滤波器来滤除一部分噪声.通过滤波处理之后得到的白噪声为限带白噪声[24]，限带白噪声功率谱密度Sx(ω)在低频的有限带宽内为恒定常数，在此频带外为零，即当|ω|≤B时，Sx(ω)=N0/2;当|ω|＞B，Sx(ω)=0.

2.2 数字平均改善信噪比的原理

2.2.1 数字平均基本原理

对于周期信号，数字平均的过程为：在每个周期内进行均匀采样多次，而且对各周期中同相位的点进行多次采样，然后对这些同相位的点进行累加及平均，从而达到压缩噪声的目的.温度信号相对于电子线路来说是一种缓变的非周期信号，非周期信号与周期信号的数字平均过程有所不同.对于非周期信号，不需要考虑周期性，只需要在有限采样时间内进行多次采样并累加及平均.因此，对于缓变非周期信号，数字平均的基本过程是先通过A/D转换器将被测信号采样值变换为数字量，然后再累加平均，以压缩噪声.数字式平均的运算过程可以表示为：为N个被测信号采样值的算术平均值，xi为第i个被测信号的采样值.

设被测信号为x(t)=s(t)+n(t)，其中s(t)为确定信号，n(t)为噪声信号.实际温度控制系统的噪声主要为高斯白噪声，设噪声的有效值为σn，对信号进行单次采样xi=si+ni，其中确定信号为si，则数字平均之前的信噪比为SNRi=si/σn.N次累加后的结果为

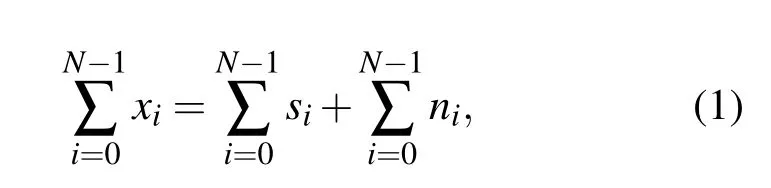
因为si是确定信号，N次累加后幅度会增加N倍.而噪声ni的幅度是随机的，累加的过程不会是简单的幅度相加，只能从其统计量的角度来考虑.采样累加后噪声的均方值为[23]

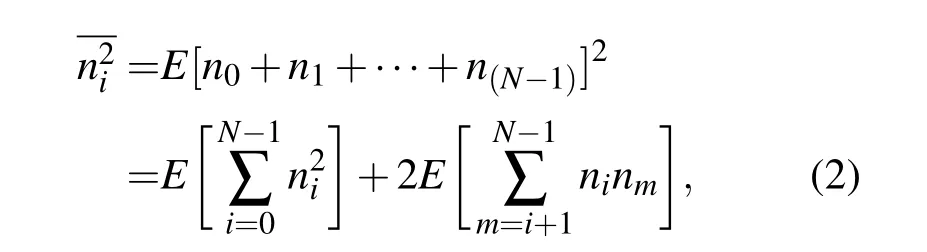
式中右边的第一项表示噪声的各次采样值平方和的数学期望值，第二项表示噪声在不同时刻的取样值两两相乘之和的数学期望值.

当噪声为白噪声，并且信号周期T足够大时，采样两点之间的时间间隔很大，不同时刻的取样值各不相关，(5)式可以简化为SNIR=√但当信号的周期很小或者采样周期很小，上式中第二项表示不同时刻噪声取样值两两相乘之和的数学期望值不为零，信噪改善比与白噪声的自相关函数有关.

2.2.2 限带白噪声的自相关函数

随机噪声x(t)的自相关函数R(t1,t2)是其时域特性的平均度量，它反映同一个随机噪声x(t)在不同时刻t1和t2取值的相关程度.如果令t1=t，t2=t+τ，则Rx(t1,t2)=Rx(t,t+τ)简记为Rx(τ)，则Rx(τ)=E[x(t)x(t+τ)].如果信号序列是由连续时间模拟信号采样得到，采样周期为Ts(相邻采样点之间的时间间隔)，则自相关函数离散形式可以写为

根据Weiner-Khintchine定理，对于有限能量的平稳随机过程，自相关函数Rx(τ)与功率谱密度函数Sx(f)之间满足傅里叶变换关系，其表示方法为[23]

即Rx(τ)和Sx(f)构成一对傅里叶变换对，当τ=0时直接可以根据自相关函数Rx(τ)求得功率为限带白噪声的功率谱密度在低频的有限带宽B内为恒定常数，在此频带外为零，即当|ω|≤B时，Sx(ω)=N0/2;当|ω|＞B，Sx(ω)=0.由此，可以得到限带白噪声的自相关函数为[24]由(10)式可以看出，系统信噪改善比是平均次数、采样周期、限带白噪声带宽的函数.

3 有限采样时间内数字式平均对温控系统信噪比的改善

对于实际温度探测与控制系统，由于温度的变化是非周期的，并且温度的变化相对于电子线路来说很缓慢.只要在总采样时间内，温度的变化不超过控制精度可以近似认为温度为一恒定值，所以数字平均必须在温度变化超出控制精度之前完成.这导致了实际温度控制系统的总采样时间有限，否则达不到实时控制的目的.

由于实际温度探测与控制系统的总采样时间有限，在总采样时间有限的情况下，平均次数(采样次数)与采样周期成反比例关系.为了讨论实际温度探测与控制系统信噪改善比与平均次数、采样周期、总采样时间的关系，我们根据数字平均对系统信噪比改善的理论推导(10)式，采用Matlab计算数字平均对系统信噪比的改善.

在对总采样时间有限的情况进行计算之前，首先对影响系统信噪改善比的两个物理量分别进行计算，这两个物理量为采样次数(平均次数)和采样周期.通常采样次数和平均次数是相同的，为了叙述方便下面用采样次数代替平均次数.因此，我们根据实际情况先对以下两种情形分别进行了计算：1)采样周期一定的条件下，改变采样次数对系统信噪改善比的影响;2)采样次数一定的条件下，改变采样周期对系统信噪改善比的影响.根据以上两种情形的分析计算，最后计算了在总采样时间一定的条件下，系统信噪改善比所能达到的饱和值以及最佳的采样次数.

3.1 采样周期一定,改变采样次数对系统信噪改善比的影响

对于温度探测与控制系统，首先将温度信号转换为电信号并进行放大、滤波，然后对模拟信号进行采样，将模拟信号转换为数字信号进行处理.若经过滤波器后，限带白噪声的带宽为B.

由(9)式可知归一化自相关函数ρ(kTs)=sin(BkTs)/(BkTs)，因为ρ(0)=1，如果不考虑ρ(0)一点，归一化自相关函数的一条包络线可以用y(k)=1/(BkTs)表示.因此，当采样周期一定时，随着间隔周期数k的增大，y(k)的值逐渐减小.另外，归一化自相关函数ρ是sinc函数，在信号与系统中，对sinc函数通常用波瓣宽度来描述.由于我们只取了对称归一化自相关函数的一半，因此，可以得到归一化自相关函数的第一波瓣(就是ρ在k＜|π/(BTs)|的部分)宽度为 2π/(BTs).由此可以看出，第一波瓣的宽度与采样周期有关.

根据以上对限带白噪声归一化自相关函数的分析，以采样周期Ts=0.0001 s，B=100 Hz为例，绘制了限带白噪声归一化自相关函数ρ与时间间隔τ之间的关系曲线，其中τ=kTs，如图1所示.

设某一时刻的白噪声为n(t)，另一时刻的白噪声为n(t+τ)，由图1可以看出，限带白噪声归一化自相关函数的包络线随着τ的增大而下降，即随着这两点之间的时间间隔的增大，限带白噪声两点之间自相关性越来越弱.

为了说明在采样周期一定条件下，改变采样次数对信噪改善比的影响，以采样周期Ts=0.0001 s，B=100 Hz为例，改变采样次数N，得到系统信噪改善比的变化，同时为了与理想白噪声相对比，绘制了理想白噪声时系统信噪改善比的变化，如图2所示.SNIR表示系统信噪改善比;SNIR′表示理想白噪声时系统信噪改善比，即SNIR′=由SNIR曲线可知，当采样周期保持不变时，采样次数越多对限带白噪声的抑制越好，即系统信噪改善比越大.从物理角度来看，随着采样次数的增加，经过累加后信号幅度会变得越强;对于噪声而言，随着采样次数的增加，采样时间间隔会变长，限带白噪声的自相关性会变弱，因此，当采样周期一定时，系统信噪改善比会随着采样次数的增加而增大.

图1 限带白噪声归一化自相关函数ρ与时间间隔τ之间的关系

图2 采样周期一定时，信噪改善比与采样次数N的关系

另外，由图2可知，当采样次数N=10000时，系统的信噪改善比SNIR=5.66，而噪声为理想白噪声时系统的信噪改善比SNIR′=100.因此，系统的信噪改善比不是简单的这是因为影响系统信噪改善比的因素不仅与采样次数有关，而且还与噪声自相关函数有关.因此，只有当采样周期足够大，采样点之间的自相关函数值很小，可以近似地认为两时刻对应的噪声之间无关，那么系统的信噪改善比SNIR=√

在实际应用中，当时间间隔τ增大到一定值时，自相关函数R(τ)已经很小，则可近似认为n(t)和n(t+τ)彼此无关.因此，引入时间τ0，当τ＞τ0时，则可以认为n(t)和n(t+τ)无关.τ0的定义为：存在τ0，使得|ρ(τ0)|≤ 0.05[25].但是由于限带白噪声归一化自相关函数是以sinc函数的规律正负振荡衰减.因此，采用归一化自相关函数的包络线来定义，若采样周期T0使得自相关函数的包络线函数1/BT0≤0.05，则当采样周期大于T0，可以认为n(t)和n(t+T0)之间无关.因此，若B=100时，则当采样周期Ts≥0.2 s，可以认为n(t)和n(t+T0)之间无关.实际应用中，要根据采样周期来确定白噪声是否能近似看作理想白噪声，当白噪声不是理想白噪声时，信噪改善比要根据(10)式来计算.

3.2 当采样次数一定,改变采样周期对系统信噪改善比的影响

由前面的分析可知，限带白噪声归一化自相关函数值随时间间隔τ的增大而减小.由于τ=k·Ts，所以，在采样次数一定的条件下，对于相同采样周期数k，采样两点之间的实际时间间隔τ随着采样周期Ts的减小而减小.

为了说明不同采样周期条件下，间隔相同采样周期数k的两点之间限带白噪声归一化自相关函数的变化，以采样次数为N=5000，采样周期分别为Ts=0.001 s，Ts=0.0001 s为例，绘制了限带白噪声归一化自相关函数ρ和间隔周期数k的关系曲线及其包络线，如图3所示.

从图3可以看出，当采样次数相同时，在采样周期分别为Ts=0.0001 s和Ts=0.001 s条件下，得到的限带白噪声归一化自相关函数值是不同的.这是因为ρ是关于τ的函数，由于τ=k·Ts，当采样周期分别为Ts=0.0001 s和Ts=0.001 s，相当于归一化自相关函数曲线分别被展宽了1/Ts倍.因此，对于相同的间隔周期数k，采样周期越小，噪声n(t)与n(t+kTs)的相关性就越大;采样周期越大，噪声n(t)与n(t+kTs)之间的相关性就越小.

为了说明采样次数一定的条件下，改变采样周期对信噪改善比的影响.以采样次数N=5000为例，采样周期从0.001—0.005 s，数字平均对系统的信噪改善比的影响，如图4所示.从图4中可以看到，当采样次数相同时，采样周期变小，信噪改善比下降.这是因为从(10)式可以看出，信噪改善比与采样次数和归一化自相关函数有关，当采样次数相同时，采样周期越小，归一化自相关函数值越大，系统信噪改善比就越小.因此，在实际应用中，采样周期越小，得到的采样值就越接近真实模拟值，但是考虑到信噪改善比的影响，采样周期越小，系统信噪改善比就越小.在充分考虑采样信号的同时，也要考虑到采样周期对系统信噪改善比的影响.

图3 限带白噪声归一化自相关函数ρ与间隔周期数k的关系曲线及其包络线

图4 采样次数一定，不同采样周期对信噪改善比的影响

3.3 总采样时间一定,系统信噪改善比的变化

当采样周期一定时，系统信噪改善比随采样次数的增加而增大;当采样次数一定时，系统信噪改善比随采样周期的减小而减小.上面分别分析了影响系统信噪比的两个物理量，但是未考虑总采样时间一定的情况.实际温度探测与温度控制系统中，总采样时间很有限.当总采样时间一定时，采样周期与采样次数成反比，若总采样时间为T，采样次数为N，则采样周期为Ts=T/N，那么(10)式可以变成：

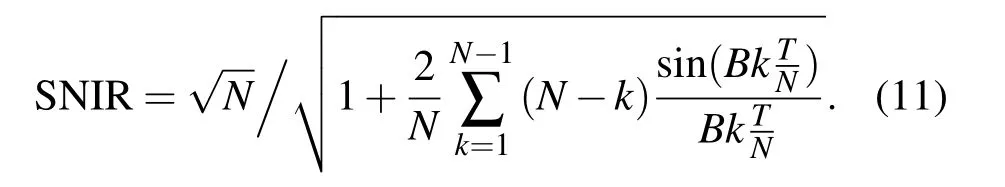
为了说明总采样时间一定条件下信噪改善比的变化，以总采样时间T=1 s，B=100 Hz为例进行说明，得到带白噪声系统信噪改善比的变化，如图5所示.

图5 总采样时间一定时，系统信噪改善比的变化

由图5可以看出，在总采样时间一定的条件下，当采样次数从1—5000时(为了清楚显示信噪改善比的变化，图中只截取了1—100次的结果)，随着采样次数增加信噪改善比增大，但是，信噪改善比会达到一定的饱和值.如图5所示，当采样次数N≥30时，信噪改善比基本上保持不变.这是因为增加采样次数虽然能够提高系统的信噪改善比，但是，当总采样时间一定时，增加采样次数就会减小采样周期;而采样周期的减小导致相邻采样点的相关性增大，根据3.2节的分析，归一化自相关函数值越大，系统信噪改善比就越小.这种相互制约的关系将导致图5所示的结果，即系统的信噪改善比会得到一个饱和值.

自相关函数是以sinc函数的规律振荡衰减，当采样周期和采样次数同时变化时，信噪改善比的上升速度会发生起伏.因此，如图5所示，当采样次数为N＜5时，1/BTs＜0.05，可以近似认为无关.当采样次数为5—20次时，信噪改善比的上升出现了上升比较快的一段，也会出现上升比较平缓的一段.

3.4 最佳采样次数

在实际工程应用中，我们不可能都用很高的采样频率，因为采样频率太高会导致硬件的开销太大，另外，微处理单元运算量增大，会增加数字系统的成本，AD采样的噪声也会随采样频率的增加而增大.由3.3节的分析可知，当系统总采样时间一定时，随着采样次数N的增加，根据(11)式，无法给出信噪改善比极限的解析式，但是，信噪改善比的增加逐渐减小并达到一个饱和值.因此，根据实际应用中精度的需要，我们可以定义，当采样次数从N-1次增加到N次时，两个不同采样次数所对应的信噪改善比的改善小于1%，那么对应的N为最佳采样次数.

4 结论

根据用于量子保密通信中单光子探测器的性能需求，针对其精密温度控制系统中微弱信号的噪声处理问题，本文研究了有限采样时间内，数字平均对温度探测与控制系统信噪改善比的影响，导出了信噪改善比与平均次数、采样周期、总采样时间的函数关系.当总采样时间一定时，信噪改善比会达到饱和值，因此给出了最佳采样次数的定义.

对于实际工程应用，当温度探测与控制系统的精度要求很高时，噪声的幅度往往超过系统分辨率，需要用数字平均来提高系统的信噪改善比，而总采样时间有限的条件下，数字平均方案实现的系统信噪改善比存在饱和值.因此，单纯地增加平均次数可能无法达到足够高的信噪改善比.这时，必须增加总采样时间，即减缓控温对象的温度变化速度.这就涉及选择热敏电阻、制冷腔的结构以及保温材料等的选择问题;当总采样时间足够大后，可以得到最佳采样次数和最佳采样周期，进而可以选择频率合适的采样器，这不仅仅会降低硬件的成本，也会使系统得到很好的信噪改善比.因此，通过对温控系统信噪改善比的分析与计算，可以指导设计过程中器件以及材料的选择来满足设计精度需求.

[1］Namekata N，Adachi S，Inoue S 2009Opt.Express17 6275

[2］Yuan Z L，Sharpe A W，Dynes J F，Dixon A R，Shields A J 2010Appl.Phys.Lett.96 071101

[3］ Wei Z J，Zhou P，Wang J D，Liao C J，Guo J P，Liang R S，Liu S H 2007J.Phys.D：Appl.Phys.40 6922

[4］Wei Z J，Li K Z，Zhou P，Wang J D，Liao C J，Guo J P，Liang R S，Liu S H 2008Chin.Phys.B 17 4142

[5］Chen X L，Wu E，Wu G，Zeng H P 2010Opt.Express18 7010

[6］Tomita A，Nakamura K 2002Opt.Lett.27 1827

[7］Ribordy G，Gautier J D，Zbinden H，Gisin N 1998Appl.Opt.37 2272

[8］Makarov V，Anisimov A，Skaar J 2006Phys.Rev.A 74 2313

[9］Lin I S，Weiner A M 2008IEEE J.Lightwave Technol.26 2692

[10］Liu J F，Liu J Y，Zhang T T，Li J C 2009Communication Networks and Services Research ConferenceMoncton，NB，May 11—13，2009 p440

[11］Kang H G，Oh J，Kwon H，Park S R，Kim S Y，Song I 2006 23rd Biennial Symposium on CommunicationsKigston Ont.，Canada，29 May—1 June，2006 p332

[12］Kim I J，Park S R，Song I，Lee J，Kwon H，Yoon S 2007IEEE Trans.Vehic.Technol.56 126

[13］Huang X G，Xu J X，He D H，Xia J L，L¨u Z J 1999Acta Phys.Sin.48 1810(in Chinese)[黄显高，徐建学，何岱海，夏军利，吕泽军1999物理学报48 1810］

[14］Dai Y，Zhang J X 2011Acta Phys.Sin.60 110516(in Chinese)[代煜，张建勋2011物理学报60 110516］

[15］Zhang W，Ge L L 2008 7th World Congress on Intelligent Control andAutomation Chongqing，China，25—27 June，2008 p7000

[16］Wang G Y，He S L 2003IEEE Trans.on Circuits and System：Fundamental Theory and Application50 945

[17］Zhao W L，Xia W，Liu P，Wang L Z 2010Acta Phys.Sin.59 2962(in Chinese)[赵文礼，夏炜，刘鹏，王林泽2010物理学报59 2962］

[18］Lacy L L，Daniel A C 1972J.Acoust.Soc.Am.52 189

[19］Shao J，Gao X M，Yuan Y Q，Yang Y，Cao Z S，Pei S X，Zhang W J 2005Acta Phys.Sin.54 4638(in Chinese)[邵杰，高晓明，袁怿谦，杨颙，曹振松，裴世鑫，张为俊2005物理学报54 4638］

[20］Zhou C L，Huang W W，Liu Y，Yang H T 2007Chin.J.Sci.Instrum.28 59(in Chinese)[周长林，黄万伟，刘勇，杨洪涛2007仪器仪表学报28 59］

[21］Wang F K，Wu J T，Liu Z G 2006J.Xi’an Jiaotong Univ.40 1006(in Chinese)[王凤坤，吴江涛，刘志刚2006西安交通大学学报40 1006］

[22］Zhou Q T，Wei J，Xu Z P 2010Infrared and Laser Engineering39 959(in Chinese)[周倩婷，危峻，徐志鹏2010红外与激光工程39 959］

[23］Gao J Z 2004The Weak Signal Detection(Beijing：Tsinghua University Press)p46(in Chinese)[高晋占2004微弱信号检测(北京：清华大学出版社)第46页］

[24］Dai Y S 1994Weak Signal Detection Methods and Apparatus(Beijing：National Defence Industrial Press)p13(in Chinese)[戴逸松1994微弱信号检测方法及仪器(北京：国防工业出版社)第13页］

[25］Wei Z J，Liao C J，Wang J D，Guo J P，Wang F Q，Liu S H 2006Acta Photon.Sin.35 1086(in Chinese)[魏正军，廖常俊，王金东，郭健平，王发强，刘颂豪2006光子学报35 1086］