基于FPGA的高斯分布随机数的生成*
姚若河 徐新才
(华南理工大学 电子与信息学院,广东 广州 510640)
蒙特卡罗模拟广泛应用于数学、计算物理学、工程技术以及经济金融等方面[1-5],用以计算多重积分、解积分方程和随机微分方程等;或者直接模拟随机过程(布朗运动、动物的生态竞争等).其收敛速度与样本数有关,与待求问题维度无关,而普通积分方法计算复杂度随着维数的增加指数增加.因此对于很多高维计算,蒙特卡罗模拟是一个非常好的计算方式.
为达到较高的模拟精度和实现实时模拟,需要大量复杂计算并且计算次数可能达到上百万次,因此需要对蒙特卡罗模拟进行硬件加速.
现场可编程门阵列(FPGA)加速相对于通用CPU 具有高度并行、速度快、功耗低等优点;而相对于ASICs,则具有设计时间短、现场可编程等优点.因此FPGA 可重构计算在蒙特卡罗模拟的硬件加速中得到了越来越多的应用.
随机数是蒙特卡罗模拟的重要模块,可分为均匀分布随机数和高斯分布随机数.均匀分布随机数常用于高斯分布随机数的产生,提供“随机性”;高斯分布随机数是应用最多的分布,可用来近似很多随机过程.高斯分布随机数产生的方法有:反函数法、变换法、拒绝-接受法和递归法等[6-9].反函数法和变换法精度较高,但计算复杂度高,硬件消耗大,设计复杂.拒绝-接受法和递归法具有结构简单、速率快的特点,但递归法输出存在相关性,拒绝-接受法输出速率不为常数.
Marsaglia 等[10]提出的基于拒绝- 接受法的Ziggurat 方法具有结构简单、设计周期短的优点.文献[11]对Ziggurat 方法进行改进后只保留了矩形区域,电路结构简单,克服了输出不恒定的缺点,但对概率密度函数(PDF)分割精度不够.文中在文献[11]的基础上,针对PDF 的尾部和顶部区域,采用嵌套分割的方法提高对尾部和顶部区域的近似精度,相对于传统Ziggurat 方法减少了设计周期和硬件资源消耗.
1 高斯分布随机数算法的改进
1.1 Ziggurat 方法基本原理
Ziggurat 方法属于拒绝-接受法,其基本原理如图1 所示[12].曲线p(x)=exp(-x2/2),x >0 为高斯分布的概率密度函数,C 为曲线p(x)与坐标轴构成的区域.Z 由图中的n-1 个矩形和1 个底部区域构成,底部区域包括底部条形区域和尾部区域,尾部区域向右延伸至无限远.其中,x(2)至x(n)为n-1个矩形的右侧边界系数,n 为构成Z 的区域的个数,各子区域的面积均为v.
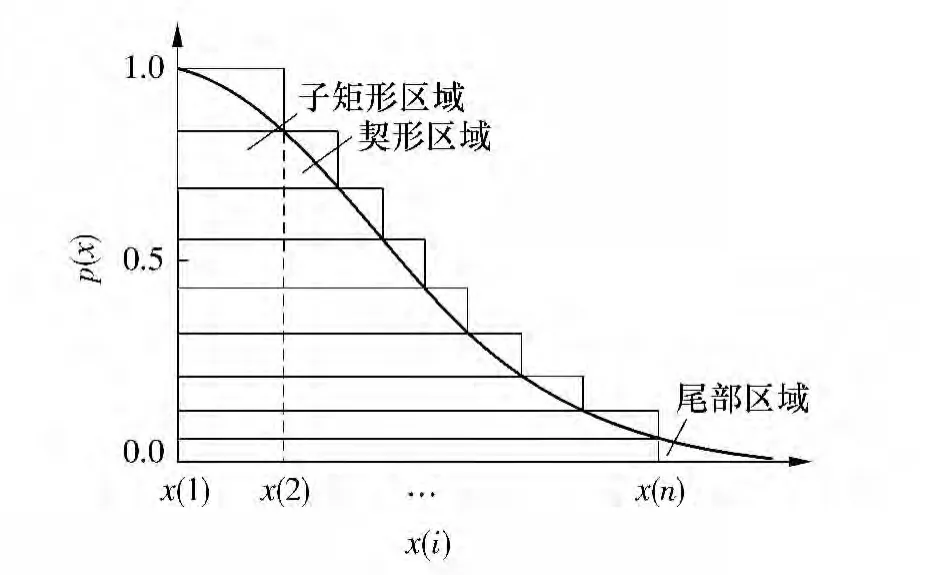
图1 Ziggurat 算法示意图Fig.1 Schematic diagram of Ziggurat algorithm
令i 为满足条件1≤i≤n 的整数,当i >1 时,为矩形区域Ri,当i=1 时为底部区域.其原理为:
(1)当i >1 时,各矩形区域Ri的右侧边界的坐标为x(i),Ri中一个随机点的横坐标为x =U1x(i).若x <x(i-1),即图1 中子矩形区域,则其必然在C中,返回对应的横坐标x.
(2)若x≥x(i-1),且在曲线p(x)下方,满足[p(x(i-1))-p(x(i))]U2<p(x)-p(x(i)),则(x,y)来自契形区域,返回x 值.
(3)若i=1,且U3<rf(r)/v,则认为x 来自底部的条形区域,否则认为来自尾部区域.
其中,U1、U2、U3为(0,1)上相互独立的均匀分布随机数.
令区域Z 最右侧矩形区域的边界系数x(n)为r(即矩形区域最大输出值),文献[11]计算得到:n取1 024 时,矩形区域占99.84%,契形区域占0.082%,尾部区域占0.086%.契形区域和尾部区域对应的概率很小,却需要计算指数、乘法、除法等复杂运算,因此文献[11]对Ziggurat 算法进行简化,只保留矩形区域,并将原算法的256 个分块提高到1024 个,简化了硬件结构.其不足是对契形区域的近似仍然不够,并且输出最大值r 仅为4.29.而在蒙特卡罗模拟中,虽然偏差较大的值出现概率很小,但对最终模拟结果影响较大.
1.2 改进后的嵌套分割算法
文中对文献[11]的方法进行了改进:
(1)首先将待求函数的概率密度函数分割为若干个矩形区域.文中先将高斯分布概率密度函数分割为顶部、中部和尾部区域,再用嵌套分割的方法将顶部和尾部区域分割为矩形区域,图2 为其分割示意图,图中x1(i)为x1层矩形边界系数.

图2 嵌套分割示意图Fig.2 Schematic diagram of nested segmentation
(2)产生概率密度函数与对应子区域相同的随机数.文中采用Ziggurat 算法中矩形系数x(i)与(0,1)上均匀分布随机数U 相乘的方法产生概率密度函数为矩形的随机数.
(3)选择对应子区域的随机数作为输出,其被选择的概率正比于子区域的面积.
新算法的特点为:①省去了Ziggurat 算法中的拒绝-接受过程,输出为常速率.②对于中部区域,将分区数从1024 提高到4096.实验发现,分块数的进一步提高对顶部和尾部精度提高很小,因此需要单独优化.③对于尾部区域,采用嵌套分割方法,最大输出值从4.29 提高到8.72.④对于顶部区域,由于每个块的面积相等,当系数绝对值较小时,矩形较高,存在较大误差.采用嵌套分割算法改进后系数差不到原有系数差的2%.
1.2.1 对顶部区域的近似
将文献[11]中的分割数提高到4 096 后,其矩形区域边界系数差lg[x(i)-x(i-1)]如图3 所示,横坐标为矩形区域边界系数序号i,纵坐标为相邻两系数的对数差lg[x(i)-x(i-1)].定义第一层为x1层,系数序号为[1,4096],示意图如图2 所示,横坐标x1(1)至x1(4096)为x1层矩形区域的右侧边界系数,纵坐标为概率密度函数.由于矩形面积恒定,系数越小,矩形区域高度越大,误差也越大.当i <220 时,系数误差大于10-4.因此对前256 个子区域进行嵌套分割.将x1层前256 个子区域分割为1024个n1层子区域,每个子区域的大小为v×256/1024.

图3 顶部区域前300 个矩形系数差Fig.3 Coefficient difference of the first 300 rectangles of top area
嵌套的第1 级为n1层,系数序号为[1,1 024],其嵌套分割示意图如图4 所示,满足x1(257)=n1(1025),n1(1)=0.其中x1(257)为图2 中x1层第257 个矩形右侧边界系数,n1(1 025)为图4 中n1层第1025 个边界系数.对n1层前128 个子区域再次进行嵌套分割得到1024 个n2层子区域.以此类推,不断对系数进行嵌套分割,使系数之差接近10-4.最终所得顶部区域只读内存ROM 地址如图5 所示.
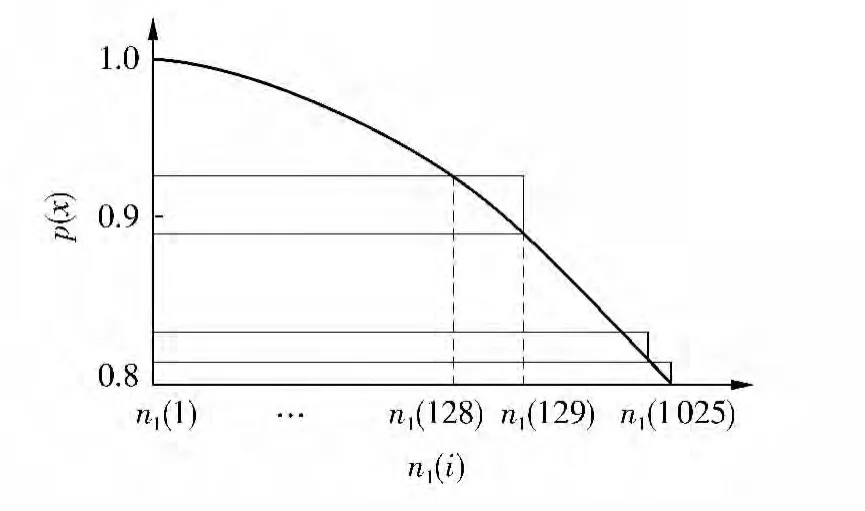
图4 顶部区域嵌套分割示意图Fig.4 Schematic diagram of nested segmentation of top region

图5 顶部区域ROM 地址Fig.5 ROM address of top region
可通过以下公式用二分法计算边界系数x(i):
尾部面积为

矩形面积为
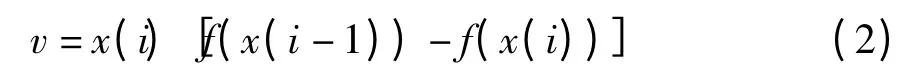
解得
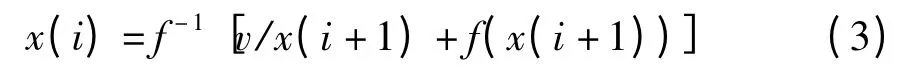
式中,r=x1(4096).
在迭代第一步,将区间[a,b]中点(a +b)/2 赋给r(a、b 为预估的r 的区间),通过式(1)计算得到v,通过式(3)迭代计算x(i).当i 在x1层迭代到i =257时,跳转到n1层,并将v 替代为vn1=v ×256/1 024,其中vn1为n1层子区域面积.跳转到n1层后再次将i 从1024 迭代到129,跳转到n2层.以此类推,得到n4层第一个系数n4(1).对区间[a,b]采用二分法不断迭代直到n4(1)=0.此时的r 即为区域Z 最右侧第4096 个矩形边界系数,即r=x1(4096)=4.39.
1.2.2 对尾部区域的近似
为提高输出的高斯分布随机数的最大值,需要对尾部区域进行嵌套分割.如图6 所示,将尾部区域分割为1 024 个子区域,通过式(3)从1 024 迭代到2,使得x2层第2 个系数等于x1层第4 096 个系数,即x2(2)=x1(4096),得到x2层最大输出值r2=x2(1024)=5.80.为进一步提高最大输出值r,继续对x2层尾部进行嵌套分割得到r3= x3(1024)=6.92,r4=x4(1024)=7.87,r5=x5(1024)=8.72….当迭代到第4 层时,r 已经超过8,因此文中采用四级迭代r=r5=8.72.相比于原算法的r=4.29,文中改进后的r 提高了107.9%.最终所得尾部区域ROM 地址分层结构如图7 所示.

图6 尾部区域嵌套分割示意图Fig.6 Schematic diagram of nested segmentation of tail region

图7 尾部区域ROM 地址Fig.7 ROM address of tail region
2 算法的硬件实现
新算法硬件系统结构见图8.

图8 改进算法系统框图Fig.8 Block diagram of the proposed method
乘法器共有两路输入,α 输入为16 位的(-1,1)上均匀分布随机数,β 输入为取自ROM 的16 位系数,两者相乘得到32 位高斯分布随机数,小数位为27 位.文中采用文献[13]中Combined Tausworthe 方法产生均匀分布随机数.
2.1 多选器选择信号的生成
图8 中的ROM 选择模块(rom_select)如图9所示.

图9 ROM 选择模块结构Fig.9 Structure of rom_select module
其中Tail_area 为尾部分割模块,输出sel_x2-sel_x5 分别是x2-x5层控制信号,rom_coef_1-rom_coef_5 分别为x1-x5层输出的系数值;Top_area 为顶部区域模块,各信号含义与Tail_area类似.Top_area 和Tail_area 输出控制信号通过Concat 模块组合为一个9 位信号,再通过ROM2 转化为多路选择器coef_mux 控制信号,选择对应的系数.
多选器选择信号通过ROM2 查找表生成,根据改进后的算法,其对应的真值见表1,0 代表低电平,1 代表高电平,X 代表0 或者1.
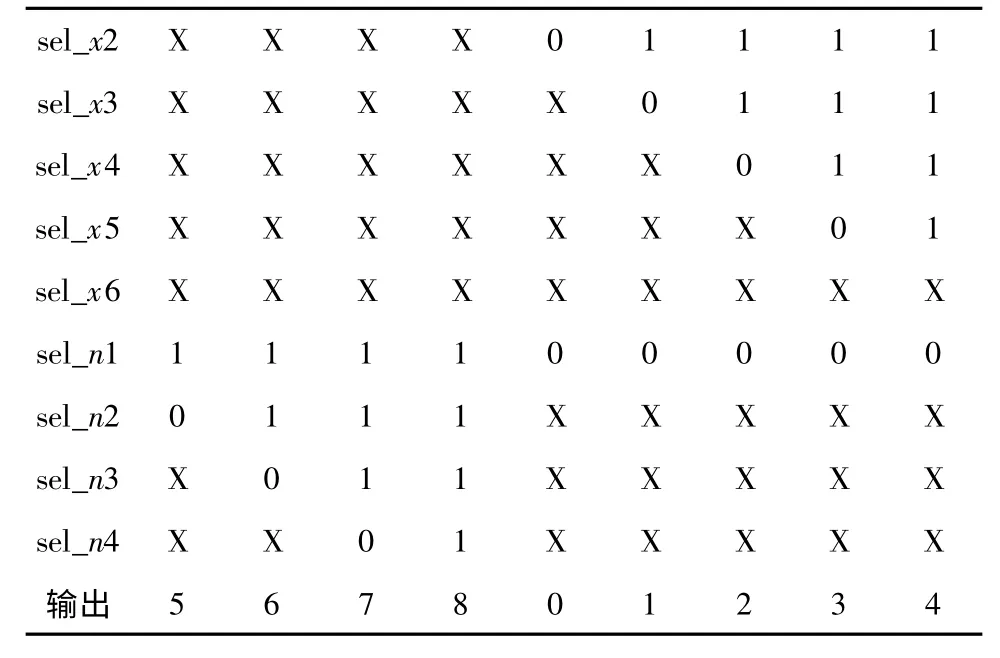
表1 ROM2 查找表Table 1 Look-up table of ROM2
2.2 ROM 选择算法的实现
由改进的算法可知,为选择对应ROM,需要对ROM 地址数据进行判断,以决定是尾部、顶部或者中部区域.下面以顶部区域为例介绍对应算法的硬件实现.
如图10 所示为顶部区域模块,自顶向下依次为n1-n4层,每层包括选择信号生成模块和系数存储单元两部分.以n1、n2层为例,其原理可描述如下.

图10 Top_area 模块示意图Fig.10 Schematic diagram of Top_area module
(1)sel_logic_n1:选择信号生成模块,Slice2 提取x1层高4 位通过sel_logic_n1 进行或非,生成n1层选择信号sel_n1,sel_n1 高电平时(此时12 位x1层地址小于256,即高4 位为低电平)跳转到n1层.
(2)n1层ROM:系数存储单元,Slice1 提取输入的n1层10 位地址信号输出到“n1层ROM”中,取出对应的系数,输出到rom_coef_n1.
(3)n2层的Slice3 提取Slice1 中的高3 位进行异或,生成n2层选择信号sel_n2,sel_n2 低电平时输出n1层系数rom_coef_n1,高电平时跳转到n2层.
2.3 整体仿真结果
在System Generator 中对硬件实现后的整体电路进行仿真,仿真结果如图11 所示.其中urn 为乘法器输入的均匀分布随机数,coef 为rom 选择模块输出的系数值,out 为乘法器输出,即文中算法生成的高斯分布随机数.
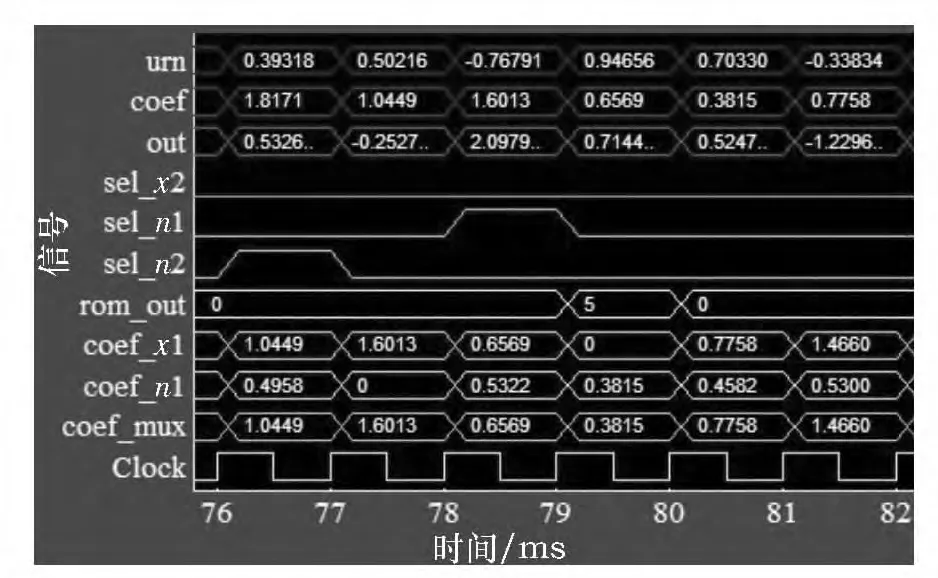
图11 电路仿真结果Fig.11 Simulation results of the circuit
sel_x2 为x2层控制信号,高电平时选择尾部区域;sel_n1 为n1层选择信号,高电平时选择顶部区域;sel_n2 为n2层选择信号.由表1 可知,3 个信号的组合“000”、“001”、“010”分别输出“0”、“0”、“5”;当rom_out 为“0”时,coef_mux 输出x1层系数coef_x1;当为“5”时,输出顶部n1层系数coef_n1.表2为改进后算法在Xilinx Virtex 4 xc4vls100 FPGA 上的综合结果,速率为270 MHz,最大输出值为8.72.
文中的嵌套分割随机数发生器所消耗的硬件资源比文献[8]基于Ziggurat 算法的硬件结构减少四分之三.在并行蒙特卡罗模拟中,若将一个蒙特卡罗模拟在M 个蒙特卡罗模拟加速器中加速,则其计算时间为单个加速器的1/M.每个加速器中随机数均为完全相同的分布,因此RAM 中的系数值也完全相同.而FPGA 中双口RAM 可同时读出两路数据,因此一组RAM 可以供两路随机数发生器使用,平均每路随机数发生器消耗12/2 =6 个块RAM,以“6(12)”列于表2 最后一行.
本算法的特点为:不仅可以生成高斯分布随机数,还可以生成概率函数从最高点向两边递减的分布函数;输出随机数最大值可以通过增加尾部嵌套层数实现,文中通过四级嵌套最大输出可以达到8.72.

表2 综合结果对比Table 2 Comparison of synthesis results
3 输出结果的统计检验
3.1 Diehard 检验
Diehard 检验包含有一系列检验[17],包括游程检验、DNA 检验、生日检验等.检验时选择检验的种类,程序返回一个P 值,如果输入文件包含的随机数为独立的随机数,则P 值应该满足在[0,1)上均匀分布.
假设x、y 服从正态分布,则
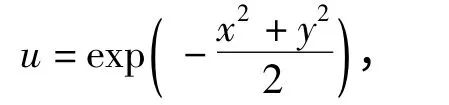
为(0,1)上均匀分布随机数.将文中嵌套分割算法所生成的600 万个高斯分布随机数转换为300 万个均匀分布随机数,部分检验结果见表3,所生成的均匀随机数通过了Diehard 检验.

表3 Diehard 检验结果Table 3 Results of Diehard tests
3.2 χ2拟合检验
χ2检验可以检验样本的概率密度函数与理论函数的差异,检验统计量为
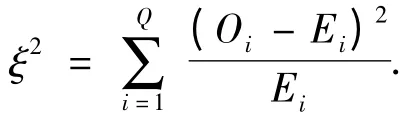
式中,Oi和Ei分别为区间i 上实际观察和理论计算得到的样本数,Q 为区间个数.原假设为样本x 服从正态分布,在原假设成立的条件下,计算ξ2对应的P值,若P 小于置信度(一般为0.05),则拒绝原假设,否则接受原假设.每次测试100 万个随机数,5 次结果见表4,均通过了统计检验.

表4 卡方检验结果Table 4 Results of Chi-squared test
其中“Matlab”为Matlab 自带“randn”函数所产生的随机数
3.3 K-S 检验
K-S 测试可以检验样本的实际积累分布函数与理论分布函数的差异[18],检验统计量为max(|F(x)-G(x)|).
原假设为样本x 服从正态分布,若原假设为真,则其值应该较小,否则应该拒绝.每次测试5 万个随机数,5 次结果见表5,通过了K-S 检验.

表5 K-S 测试结果Table 5 Results of K-S test
3.4 相关性检验
如果相邻输出存在相关性,则其输出存在规则的晶格结构[16].文中算法产生的随机数散点图(Ui,Ui+1)如图12 所示,没有明显的相关性.
在Matlab 中计算改进后算法生成的两万个随机数的±2000 个lag 对应的自相关函数.如图13 所示,除原点外其他点归一化后的自相关函数接近0,没有明显的相关性.

图12 生成随机数的散点图Fig.12 Scatter plot of generated random numbers

图13 生成随机数的自相关函数Fig.13 Autocorrelation function of generated random numbers
4 结语
文中针对Ziggurat 算法输出速率不恒定、算法中出现概率很小的支路却占用大量的硬件资源和设计复杂等问题,对高斯分布的概率密度函数进行矩形嵌套分层分割,对每一个矩形块采用Ziggurat 中算法生成概率密度函数为矩形的随机数.针对仿真中出现的极值情况,对尾部区域进行了优化处理,最大输出可以达到8.72.统计检验结果表明,新嵌套分割算法生成的随机数为独立不相关的高斯分布随机数.
[1]Luu J,Redmond K,Lo W C Y,et al.FPGA-based Monte Carlo computation of light absorption for photodynamic cancer therapy[C]∥Proceedings of 17th IEEE Symposium on Field Programmable Custom Computing Machines.Napa:IEEE Computer Society,2009:157-164.
[2]Simon A,Tudoran R,Cret O,et al.FPGA-based Monte-Carlo computation of the electric potential in homogeneous and non-homogeneous spaces[C]∥Proceedings of the 8th FPGA World Conference.New York:ACM,2011:63-68.
[3]Castillo J V,Atoche A C,Longoria-Gandara O,et al.An efficient Gaussian random number architecture for MIMO channel emulators[C]∥Proceedings of IEEE Workshop on Signal Processing Systems.Beirut:IEEE,2011:316-321.
[4]Sanchez-Roman D,Moreno V,Lopez-Buedo S,et al.FPGA acceleration using high-level languages of a Monte-Carlo method for pricing complex options[J].Journal of Systems Architecture,2013,59(3):135-143.
[5]de Schryver C,Shcherbakov I,Kienle F,et al.An energy efficient FPGA accelerator for Monte Carlo option pricing with the Heston model[C]∥Proceedings of International Conference on Reconfigurable Computing and FPGAs.Cancun:IEEE,2011:468-474.
[6]Lee D U,Cheung R C C,Villasenor J D,et al.Inversionbased hardware Gaussian random number generator:a case study of function evaluation via hierarchical segmentation[C]∥Proceedings of IEEE International Conference on Field Programmable Technology.Bangkok:IEEE,2006:33-40.
[7]Fung E,Leung K,Parimi N,et al.ASIC implementation of a high speed WGNG for communication channel emulation[C]∥Proceedings of IEEE Workshop on Signal Processing Systems Design and Implementation.Austin:IEEE,2004:304-309.
[8]Zhang G,Leong P H W,Lee D U,et al.Ziggurat-based hardware Gaussian random number generator[C]∥Proceedings of International Conference on Field Programmable Logic and Applications.Tampere:IEEE,2005:275-280.
[9]Lee D U,Luk W,Villasenor J D,et al.A hardware Gaussian noise generator using the Wallace method[J].IEEE Transactions on Very Large Scale Integration (VLSI)Systems,2005,13(8):911-920.
[10]Marsaglia G,Tsang W W.The Ziggurat method for generating random variables[J].Journal of Statistical Software,2000,5(8):1-7.
[11]王灵芝.用FPGA 产生高斯随机数及其在量子密码中的应用[D].福州:福州大学物理与信息学院,2006:17-19.
[12]Thomas D B,Luk W,Leong P H W,et al.Gaussian random number generators [J].ACM Computing Surveys(CSUR),2007,39(4):11/1-38.
[13]L’Ecuyer P.Maximally equidistributed combined Tausworthe generators [J].Mathematics of Computation,1996,65(213):203-213.
[14]Lee D U,Villasenor J D,Luk W,et al.A hardware Gaussian noise generator using the Box-Muller method and its error analysis[J].IEEE Transactions on Computers,2006,55(6):659-671.
[15]Thomas D B,Luk W.Efficient hardware generation of random variates with arbitrary distributions[C]∥Proceedings of IEEE Symposium on Field-Programmable Custom Computing Machines.Napa:IEEE,2006:57-66.
[16]Malik J S,Malik J N,Hemani A,et al.Generating high tail accuracy Gaussian random numbers in hardware using central limit theorem[C]∥Proceedings of IEEE/IFIP 19th International Conference on VLSI and Systemon-Chip.Hong Kong:IEEE,2011:60-65.
[17]L' Ecuyer P.Random number generation[M].Heidelberg:Springer,2012:21-23.
[18]Knuth D E.The art of computer programming,vol.2:seminumerical algorithms[M].Massachusetts:Addison_Wesley,1981:48-55.

