二维粘弹性不可压分析在扩展有限元中的实现①

顾志旭，郑 坚，彭 威，殷军辉

(军械工程学院火炮工程系，石家庄 050003)

0 引言

裂纹作为影响固体火箭发动机药柱结构完整性的重要因素，长期以来受到广泛关注。传统有限元法在处理断裂问题时存在着固有缺陷，如裂纹面和裂尖必须位于单元边和单元节点上，裂纹只能沿单元边界扩展，扩展时需重新划分网格等［1－2］。此外，为获得较为精确的结果，往往需要对裂纹局部的网格进行加密处理，大大增加了计算成本。针对上述弊端，1999年，Belytschko和Möes基于单位分解思想对传统有限元进行了重要的改进，提出了一种新的计算方法－扩展有限元法(XFEM)［3－4］。该方法是在常规有限元位移模式中，加入了能够反映裂纹面不连续性的阶跃函数和裂尖局部特性的渐进位移场函数，使得非连续体的几何构型完全独立于网格，无需对裂纹局部的网格加密处理，同时也避免了传统有限元重复划分网格的不便。应用扩展有限元法，Belytschko等［5］成功模拟了裂纹分叉和扩展，Sukumar等［6］模拟了含孔洞和夹杂的非均匀材料，Gracie等［7］首次实现了在细观尺度上二维和三维固体材料中的位错的有限元模拟。方修君等［8］提出了基于扩展有限元法的粘聚裂纹模型，并用于重力坝地震开裂过程。Zhuang Z等［9］基于连续体的壳单元建立了新的壳体扩展有限元格式。此外，在剪切带演化［10］、多相流［11］、纳米界面力学［12］、多尺度模拟［13］等方面也有广泛的应用。经十多年的发展完善，扩展有限元法逐渐成为了一种处理非连续场、局部变形和断裂等复杂力学问题的功能强大、极具应用前景的新方法［14］。

固体推进剂的泊松比接近0.5，是一种近似不可压缩的粘弹性材料。采用基于Herrmann泛函建立的不可压和近似不可压粘弹性增量有限元法［15－16］分析时，可避免计算中出现体积“自锁”的现象，且计算准确度较好。然而，该方法是在传统有限元位移模式建立的，在分析断裂问题时，仍然会遇到网格划分不便的问题。

本文基于单位分解思想，将由Herrmann泛函建立的不可压和近似不可压粘弹性增量有限元法推广至扩展有限元模式下，充分结合了前者计算精度高和后者网格划分(前处理)简洁的优势。最后给出一个算例，结果表明了本文方法的有效性和便捷性。

1 扩展有限元与粘弹性不可压增量有限元

1.1 扩展有限元的位移模式

扩展有限元法分析断裂问题时，先不考虑裂纹面的位置，直接划分网格，然后应用单位分解法的思想，对裂纹周围的节点自由度进行加强。对于平面裂纹，裂纹面的近似位移为

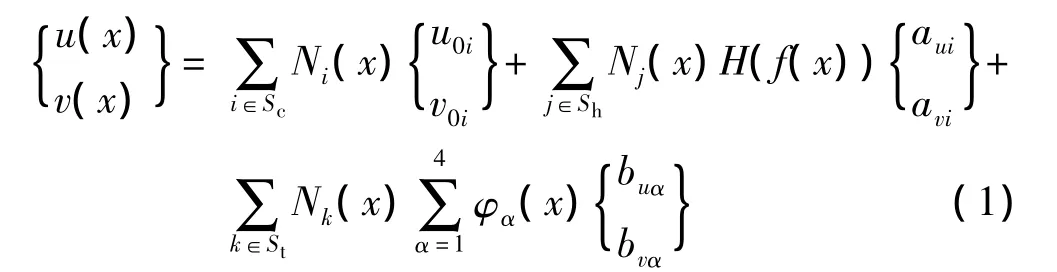
式中 Sc为所有常规单元节点的集合;Sh为完全被裂纹贯穿的单元节点的集合(图1中小方块表示的节点);St为含裂尖单元节点的集合(图1中小圆圈表示的节点);{u0i，v0i}T、{aui，avi}T和{buα，bvα}T分别为常规单元节点、贯穿单元节点和裂尖单元节点的位移;Nl(x)(l=i，j，k)为常规有限元中的形函数;H(f(x))为阶跃函数;φα(x)为裂尖渐进位移函数。

阶跃函数H(f(x))用来反映裂纹面位移的不连续性，定义为

式中 f(x)为符号距离函数构造的水平集函数。

裂尖渐进位移函数φα(x)用来反映裂尖区域的局部特性，常取裂纹位移解析解的各项，即

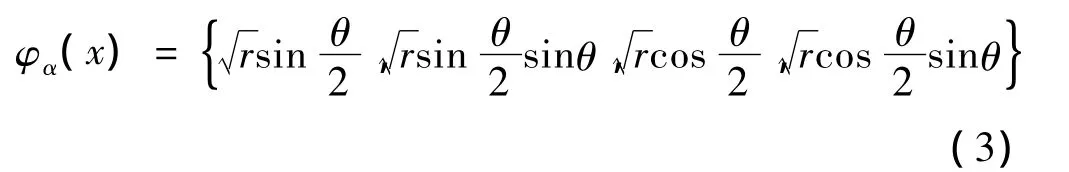
式中 r、θ为裂尖局部极坐标。

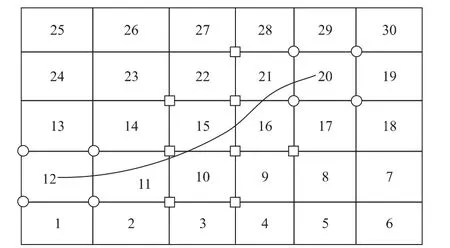
图1 网格中的任意裂纹Fig.1 An arbitrary crack placed on a mesh

在扩展有限元中，节点自由度对应着局部近似空间的基函数系数［17］。St、Sh、Sc集中的节点在每个常规自由度方向分别增加4、1、0个自由度，则节点的广义自由度分别为 10、4、2。

1.2 粘弹性不可压有限元法

Herrmann通过引入平均应力函数，将经典弹性本构方程修改为方程(4)和方程(5)，解决了泊松比等于0.5时方程出现奇异的问题。

利用上述本构关系建立有限元列式时，因平均应力函数R的引入，单元内增加了一个单自由度的节点［15］。对于平面问题，单元的广义节点位移列阵U和单元位移列阵u分别为

此时，形函数矩阵为

对于粘弹性材料，将松弛模量表示为Prony级数形式:

利用Herrmann变分原理，粘弹性对应原理及虚功原理，推导得出粘弹性不可压增量有限元法的支配方程［15－16］:

其中

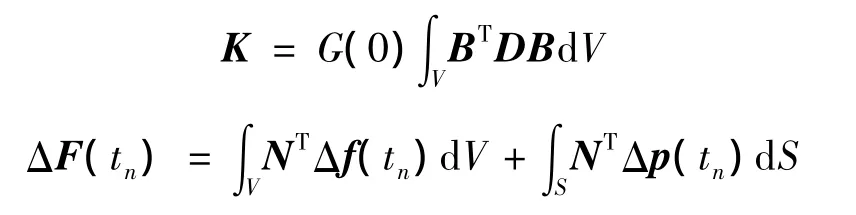
平均应力函数R的引入，使单元内增加了一个单自由度的节点，可视为对传统有限单元进行的增强处理，但这不同于上文介绍的扩展有限元法。相比于传统有限元法，扩展有限元法只是增加了部分节点的自由度，并未增加节点的数目。上述不可压粘弹性有限元法则相反，不改变原有节点的自由度，而在全体单元内增加一个节点。前者是局部增强，实现便捷地划分网格，后者是全局增强，实现不可压材料的准确分析。

2 扩展有限元中的粘弹性不可压法

2.1 有限元列式与相关矩阵

在扩展有限元模式下，基于本构方程(4)、(5)建立粘弹性不可压法的支配方程的方法同文献［15－16］。难点在于确定刚度矩阵K、形函数矩阵N、应变矩阵B及载荷列阵F等矩阵的具体形式。为便于说明，对图1中的单元进行编号。图中不含自由度增强节点的单元，如25号单元，相关矩阵见文献［15］。本文只讨论含增强型节点的单元，如9、12、15、16、21 号单元。

首先，分析裂尖所在的12号单元。依据式(1)，单元内节点k(k=i，j，m，n为单元节点局部编号，下同)的位移向量为

考虑到引入的平均应力函数R，单元广义节点位移列阵应为

单元内任一点的广义位移同式(7)。

形函数矩阵整体形式同式(8)，但因节点自由数的增加，结合式(1)为

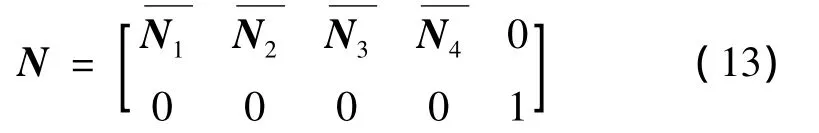
其中

Nl=(1+ξlξ)(1+ηlη)/4 为常规矩形单元的形函数。

应变矩阵依据式(12)、式(13)及几何方程得出:

则，单元内任一点的应变为

可见，因节点及节点自由度数的增加，形函数矩阵N和应变矩阵B的规格相比于传统有限元中的规格有所增加。为便于下文推导，依据B矩阵的特点，对弹性矩阵D进行分块处理，即

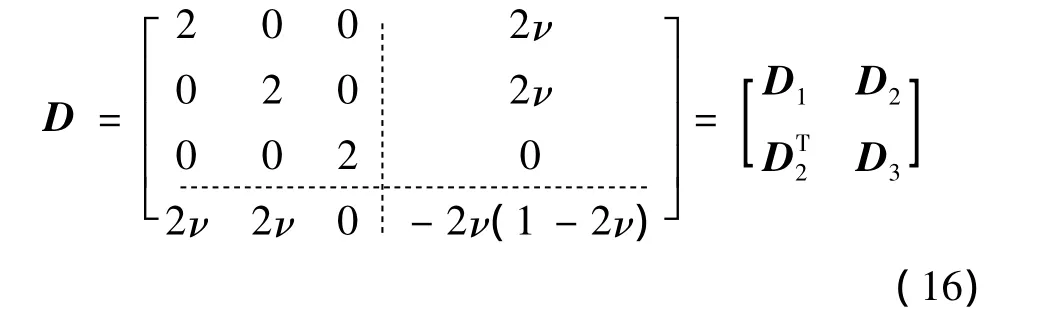
将式(16)代入式(10)中刚度矩阵公式，得

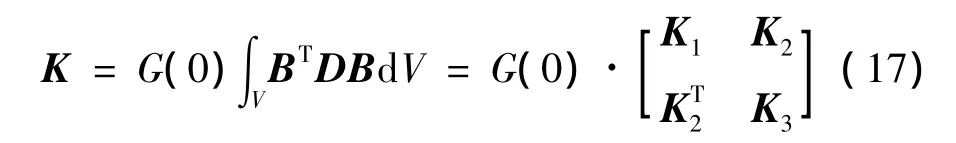
其中

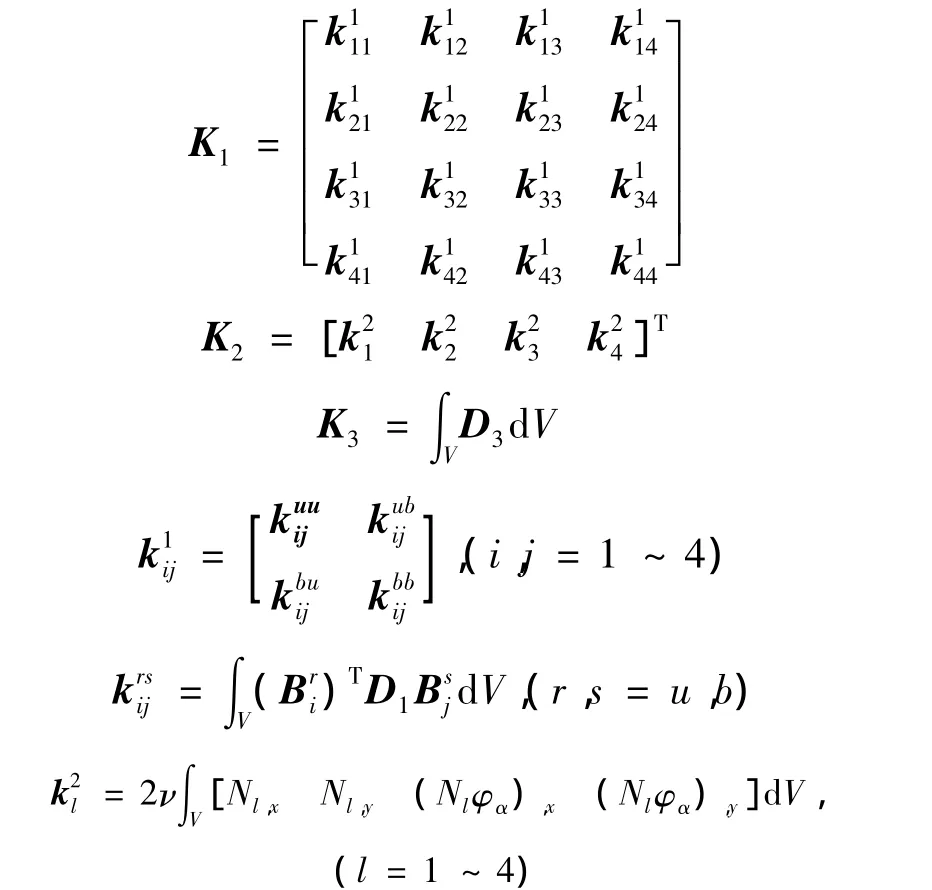
单元广义节点载荷列阵为

其中，Fk(k=i，j，m，n)为广义等效节点载荷，由式(19)确定:

式中 f=［fu，fv，0］T、p=［pu，pv，0］T分别称为广义分布体力和广义分布面力，0分量对应于广义位移中的R分量［15］。

由式(17)、式(12)及式(18)求得裂尖12号单元的刚度矩阵K、广义节点位移列阵U及广义节点载荷列阵F后，利用式(10)可对此单元进行分析。

其他含有增强型节点的单元处理方法相似，关键在于确定广义节点列阵U、形函数矩阵N及应变矩阵B，下文以裂纹穿透的15单元为例补充说明。

15号单元为裂面增强型单元，根据式(1)，节点k的位移向量为

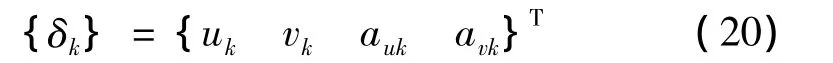
单元广义节点位移列阵同(12)式，形函数矩阵N与应变矩阵B的整体形式同式(13)、式(14)，但其中的分量不同，如下式所示:

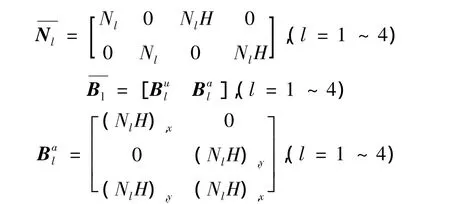
在求解应变矩阵时需要对形函数求偏导，这里直接给出结果［18］:

其中，φα，x、φα，y通过坐标变换，由裂尖局部坐标系下的偏导获得，即

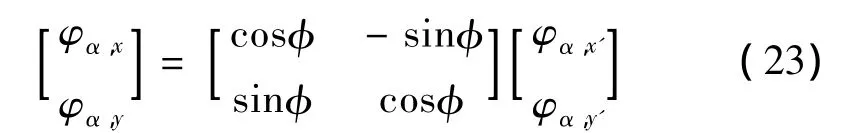
式中 φ为裂尖切线与全局坐标系x轴之间的夹角。

φα，x'、φα，y'由以下分量确定:

2.2 应力强度因子的求解

在扩展有限元中直接求解应力强度因子K时，需要借助于相互作用积分［4］:

在裂尖区域，相互作用积分I(1，2)与真实变形场和附加变形场的应力强度因子K有如下关系:

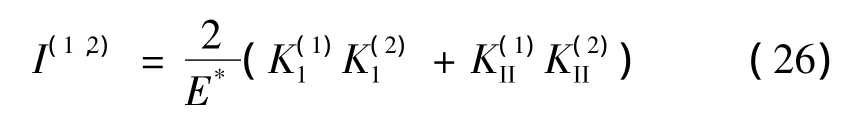
式中 平面应力时E*=E(弹性模量)，平面应变时E*=E/(1－ν2)，ν为泊松比。

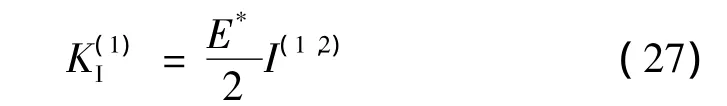
3 算例

为了验证本文方法的合理性，以一受拉的带单边裂纹的矩形平板为例进行试算，见图2。

图2 含单边裂纹的受拉板Fig.2 An edge-cracked plate under tension

相关参数为:σ =10 Pa，L/W=16/7，a/W=1/2，W=0.07 m。板的粘弹性由Burgers模型描述，见图3。其中，E1=0.495 MPa，E2=4.854 MPa，η1=1 × 1015MPa·s，η2=1.55 ×103MPa·s。

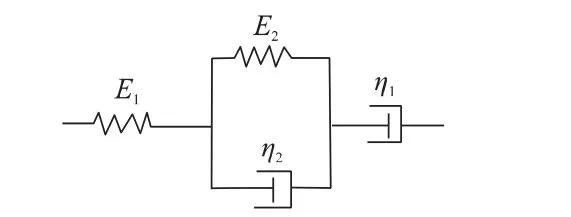
图3 Burgers模型Fig.3 Burgers model

前文建立有限元列式时，用到了松弛模量的Prony级数形式。对此，由四参量的Burgers模型求得级数形式的松弛模量［19］:

此问题的解析解为

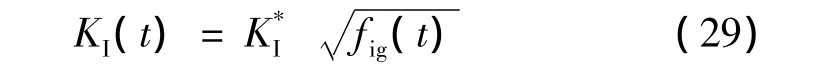
式中 KI(t)为蠕变断裂应力强度因子［20］为线弹性应力强度因子，由文献［21］给出;fig(t)为能量释放率的时间因子［20］。

不同泊松比(不同程度的近似不可压性)下，裂纹的蠕变应力强度因子的计算结果见图4。其中，图4(a)给出了ν=0.495时的解析解、本文解以及常规有限元解。可知，蠕变开始时刻t=0时，三者分别为9.386 2、9.255 2、9.257 6 Pa·m1/2较吻合。随着蠕变的进行，本文解和解析解趋近于15.916 8 Pa·m1/2，而常规有限元解趋于15.697 7 Pa·m1/2，比本文解误差大。图4(b)用解析法和本文法计算了 ν分别为0.400、0.450、0.500 时的蠕变应力强度因子。结果表明，在蠕变初期(0＜t＜120)，不同泊松比下应力强度因子相近。随着时间的推移，泊松比的影响逐渐凸显，最终蠕变应力强度因子趋于不同值。图4(c)计算了ν分别为0.490和0.499时的蠕变应力强度因子，两者变化规律与图4(a)和(b)相同。从结果来看，泊松比相差1.84%，最终应力强度因子相差2.75%。可见，在此种工况下，粗略计算时泊松比精确到小数点后第二位即可。此外，图4(a)～(c)中均表现出本文解的误差，在蠕变起始阶段和稳定阶段均小于中间阶段。这主要是由Burgers模型转换得到的松弛模量中级数项数较少，粘弹性表征不足所致。

综上所述，对于弹性材料泊松比对应力强度因子的影响较小(t=0 s时刻，蠕变未发生时，不同泊松比下所得应力强度因子近似为同一值，曲线起始于同一点)，而对于粘弹性材料，随着蠕变的发生，不同泊松比的影响逐渐放大。因此，对粘弹性断裂问题，如果仅关注短时响应，粗略计算时，可忽略泊松比变化的影响。如果关注长时响应，就必须考虑泊松比大小的影响。

图4 蠕变载荷下的应力强度因子Fig.4 Variation of SIF under creep loading

4 结论

(1)尝试将基于Herrmann泛函建立的不可压和近似不可压粘弹性增量有限元法，推广至扩展有限元模式。这样在有限元分析粘弹性材料的断裂问题时，将不受泊松比和网格划分的限制，既保证了计算的准确度，同时又降低了有限元前处理的难度。算例结果表明了该方法的有效性和便捷性。

(2)以四节点矩形单元为例建立了有限元列式，但该方法并不受单元类型的限制，适用于任意节点的二维单元。在选择裂尖增强单元时，本文只选取了1层，而在实际应用时，为提高计算精度，往往选择多层单元，文中方法仍可推广。

(3)本文的工作只表明该方法可行，所建有限元列式仅能用于二维分析。如要对推进剂药柱结构分析，鉴于其结构和载荷的复杂性，必须要建立三维的有限元列式，进行三维分析，这将是下一步的工作。

［1］茹忠亮，朱传锐，张友良，等.断裂问题的扩展有限元法研究［J］.岩土力学，2011，32(7):2171－2176.

［2］郭历伦，陈忠富，罗景润，等.扩展有限元方法及应用综述［J］.力学季刊，2011，32(4):612－625.

［3］Belytschko T，Black T.Elastic crack growth in finite elements with minimal re－meshing［J］.Int.J.Numer.Meth.Engng.，1999，45(5):601－620.

［4］Möes N，Dolbow J，Belytschko T.A finite element method for crack growth without remeshing［J］.Int.J.Numer.Meth.Engng.，1999，46:131－150.

［5］Belytschko T，et al.Dynamic crack propagation based on loss of hyperbolicity and a new discontinuous enrichment［J］.Int.J.Numer.Meth.Engng.，2003，58:1873－1905.

［6］Sukumar N，et al.Modeling holes and inclusions by level sets in the extended finite－element method［J］.Computer Methods in Applied Mechanics and Engineering，2001，190(46－47):6183－6200.

［7］Gracie R，Oswald J，Belytschko T.On a new extended finite element method for dislocations:Core enrichment and nonlinear formulation［J］.Journal of the Mechanics and Physics of Solids，2008，56(1):200－214.

［8］方修君，金峰，王进挺.基于扩展有限元法的Koyna重力坝地震开裂过程模拟［J］.清华大学学报，2008，48(012):2065－2069.

［9］Zhuang Z，Cheng B B.A novel enriched CB shell element method for simulating arbitrary crack growth in pipes［J］.Science China Physics，Mechanics ＆ Astronomy，2011，54(8):1520－1531.

［10］Samaniego E，Belytschko T.Continuum－discontinuum modelling of shear bands［J］.Int.J.Numer.Meth.Engng.，2005，62(13):1857－1872.

［11］Chess J，Belytschko T.An extended finite element method for two－phase fluids:Flow simulation and modeling［J］.Journal of Applied Mechanics，2003，70(1):10－17.

［12］Farsad M，Vernerey F J，Park H S.An extended finite element/level set method to study surface effects on mechanical behavior and properties of nanomaterials［J］.Int.J.Numer.Meth.Engng.，2010，84(12):1466－1489.

［13］Belytschko T，Gracie R，Ventura G.A review of extended/generalized finite element methods for material modeling［R］.Modeling and Simulation in Materials Science and Engineering，2009，17(043001).

［14］庄茁，柳占成，成斌斌，等.扩展有限单元法［M］.北京:清华大学出版社，2012.

［15］张海联，周建平.固体推进剂药柱的近似不可压缩粘弹性增量有限元法［J］.固体火箭技术，2001，24(2):36－40.

［16］田四朋，雷勇军，李道奎，等.固体火箭发动机药柱不可压和近似不可压三维分析［J］.固体火箭技术，2006，29(6):395－399.

［17］金峰，方修君.扩展有限元法及与其他数值方法的联系［J］.工程力学，2008，25(1):1－16.

［18］Soheil Mohammadi.Extended Finite Element Method［M］.Blackwell Publishing Ltd.，2008.

［19］潘晓明，余俊，杨钊，等.一种将线性粘弹性微分型本构方程应用到ABAQUS的方法［J］.华侨大学学报，2010，31(5).

［20］张淳源.粘弹性断裂力学［M］.武汉:华中理工大学出版社，1992.

［21］赵建生.断裂力学及断裂物理［M］.武汉:华中科技大学出版社，2003:126.