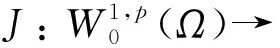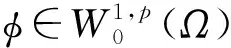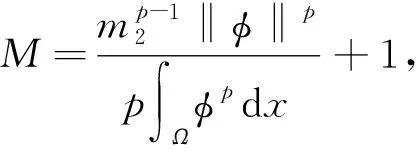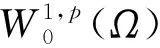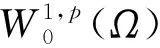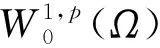p-Kirchhoff型方程解的多重性
李 健,杜泊船,赵 昕,吕显瑞
(1.吉林农业大学 信息技术学院,长春 130118;2.吉林大学 生命科学学院,长春 130012;3.吉林大学 数学学院,长春 130012)
0 引言与主要结果
考虑如下p-Kirchhoff型方程:
(1)

Kirchhoff模型[1]为
该模型可用于描述生物的种群密度等平均量,其对应的稳态Kirchhoff型方程为
(2)
关于方程(2)的研究目前已有许多结果[2-4].文献[5-8]应用变分法研究了问题(1)的非平凡解.显然,方程(1)是方程(2)的推广.事实上,当M(t)=a+bt,p=2时,方程(1)即为方程(2)的情形.此外,当M(t)=1时,方程(1)可转化为
(3)

0<μF(x,s)≤f(x,s)s, ∀s>0, ∀x∈Ω
满足时,得到了方程(1)正解的存在性.本文在该条件不满足时研究方程(1)解的多重性,得到如下结果.

(H0) 存在常数0 (H1) 存在正常数C1,C2和q∈(p,p*),使得 (H4) 存在C*>0,使得P(x,t)≤P(x,s)+C0,∀0 注1文献[6]在超线性幂次次临界增长且对称情形下得到了方程(1)的无穷多解; 文献[8]在非线性项满足渐近线性增长情形下得到了方程(1)的两个非平凡解;文献[7]研究了方程(1)在临界增长情形下解的存在性.注意文献[5]中(AR)条件结合次临界增长条件导致非线性项满足超线性次临界增长,而在定理1的条件下,该条件不满足但非线性项仍满足超线性次临界增长条件. 这里 范数定义为 定义1如果 显然若u为J的临界点,则u是方程(1)的弱解.本文将利用山路引理得到问题(1)非平凡解的存在性. 定义 相应的泛函定义为 类似地,定义 相应的泛函定义为 下面只考虑得到正解的存在性,类似地,可以得到负解的存在性.由推广形式的山路定理[11],只需证明泛函J+具有山路几何并且满足(C)c条件. 先证明泛函J+具有山路几何,即: 引理1在定理1的假设下,有: 证明: 1) 由(H1),(H2),对任意的>0,存在C>0,使得 ∀x∈Ω, ∀s>0. 因此,结合(H0),应用Sobolev嵌入与Poincare不等式,可得到常数σ1,C1>0,使得 由q>p易知,存在r,δ>0,使得结论1)成立. 2) 由(H3),对任意的M>0,存在CM>0,使得 F+(x,s)≥Msp-CM, ∀x∈Ω, ∀s>0. (4) 在定理1的假设下,(PS)条件不满足.下面证明泛函J满足(C)c条件. 引理2在定理1的假设下,泛函J+满足(C)c条件. 证明: 假设{un}n∈⊂为(C)c序列,即 J+(un)→c∈, (1+‖un‖)‖(J+)′(un)‖→0,n→+∞. (5) 并且有|wn(x)|≤h(x),a.e.x∈Ω,其中h∈Lp(Ω). 下证在Ω中w0(x)=0 a.e.事实上,记Ω0∶={x∈Ω:w0(x)≠0}.若Ω0≠Ø,则有|un(x)|→+∞,∀x∈Ω0.由假设(H3)和式(5)知, (6) 关于x∈Ω一致成立.由(H6)、 式(5)及Fatou引理,有 这与式(6)矛盾,从而|Ω0|=0.因此w0(x)=0 a.e.x∈Ω. (8) 由 并结合式(8)可得 由(H4)可得 另一方面,由假设(H1),(H2),对任意的R0>0,有 当n充分大时,矛盾. 由(H1),(H2)与Sobolev嵌入定理可得 (10) 记 由|((J+)′(un),un-u0)|→0,结合式(10)可得Qn→0. 另一方面,注意到 结合弱收敛un⇀u0及不等式 应用(H6)可知存在常数C2>0,使得 [1] Kirchhoff G.Mechanik [M].Leipzig: Teubner,1883. [2] CHENG Bi-tao,WU Xian,LIU Jun.Multiple Solutions for a Class of Kirchhoff Type Problems with Concave Nonlinearity [J].Nonlinear Differ Equ Appl,2012,19(5): 521-537. [3] MAO An-min,ZHANG Zhi-tao.Sign-Changing and Multiple Solutions of Kirchhoff Type Problems without the P.S.Condition [J].Nonlinear Anal: Theory,Methods &Applications,2009,70(3): 1275-1287. [4] Perera K,ZHANG Zhi-tao.Nontrivial Solutions of Kirchhoff-Type Problems via the Yang Index [J].J Differential Equations,2006,221(1): 246-255. [5] Corrêa F J S A,Figueiredo G M.On an Elliptic Equation ofp-Kirchhoff Type via Variational Methods [J].Bull Austral Math Soc,2006,74(2): 263-277. [6] Corrêa F J S A,Figueiredo G M.On ap-Kirchhoff Equation via Krasnoselskii’s Genus [J].Appl Math Lett,2009,22(6): 819-822. [7] Hamydy A,Massar M,Tsouli N.Existence of Solutions forp-Kirchhoff Type Problems with Critical Exponent [J].Electron J Differential Equations,2011,105: 1-8. [8] LIU Du-chao,ZHAO Pei-hao.Multiple Nontrivial Solutions to ap-Kirchhoff Equation [J].Nonlinear Anal: Theory,Methods &Applications,2012,75(13): 5032-5038. [9] Gasiński L,Papageorgiou N S.Multiple Solutions for Asymptotically (p-1)-Homogeneousp-Laplacian Equations [J].J Funct Anal,2012,262(5): 2403-2435. [10] OU Zeng-qi,LI Chun.Existence of Solutions for Dirichlet Problems withp-Laplacian [J].Nonlinear Anal: Theory,Methods &Applications,2012,75(13): 4914-4919. [11] Schechter M.A Variation of the Mountain Pass Lemma and Applications [J].J London Math Soc,1991,44(3): 491-502.
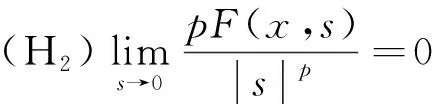

1 定理1的证明