集值优化Henig有效元广义二阶组合切上图导数的最优性条件

徐义红,张小荣,汪 涛

(南昌大学 数学系,南昌 330031)

集合的锥有效性是向量优化的重要组成部分.由于(弱)有效性范围较大,收缩解的范围即成为向量优化的一项主要工作,因此各种真有效性的概念被相继引入[1-2],其中Henig有效性[1]是具有代表性的真有效性之一.Henig真有效点既保持了超有效点的主要特征,同时它仅要求序锥具有基,而且存在条件比超有效点弱得多,因而研究向量优化的Henig有效解已成为优化理论的主要内容[3-4].仇秋生[4]得到了Henig真有效点的若干等价条件,并讨论了Henig真有效点与Benson真有效点间的关系;余国林等[5]在赋范线性空间中对集值映射引入了锥-Henig有效次梯度和Henig有效次微分的概念.

目前,用切导数研究集值优化问题的最优性条件已取得一系列成果[6-9].Jahn等[7]提出了广义二阶切上图导数并建立了二阶最优性条件.二阶切集仅是闭集,通常不是锥,即使对于凸集,它的二阶切集也未必是凸集.而广义二阶切上图导数[7]是通过二阶切集引进的,因而广义二阶切上图导数不具有广义切上图导数的某些性质.为克服此二阶导数的某些局限性,李声杰等[8]引进了一种新的广义二阶切上图导数----广义二阶组合切上图导数(generalized second-order composed contingent epiderivative),在某种假设下证明了存在性定理,利用该导数得到了集值优化问题的最优性条件,推广了相关结论.广义二阶组合切上图导数的性质[8]: 在某种假设下,它是严格正齐次和次可加的.

本文利用广义二阶组合切上图导数建立集值优化问题Henig有效元高阶导数的最优性条件.

1 基本概念

设X,Y为实赋范线性空间,Y*为Y的拓扑对偶空间.设M是Y的任一非空子集,用intM,clM和coneM分别表示M的内部、 闭包和生成锥,其中

coneM={λm:λ≥0,m∈M}.

记C为Y中顶点在原点的闭凸点锥.如果0∉clΘ且C=coneΘ,则凸子集Θ⊂C称为C的基,δ=inf{‖θ‖|θ∈Θ}>0.设B是Y中的闭单位球,即B={y∈Y|‖y‖≤1}.对ε∈(0,δ),定义

Sε(Θ)=cone(Θ+εB),Cε(Θ)=clcone(Θ+εB).

引理1[10]设0≤ε1<ε2<δ,则Cε1(Θ){0}⊂intCε2(Θ).

引理2[2]设0<ε<δ,则Cε(Θ)是闭凸点锥.

定义1[1]设M是Y的非空子集,若存在ε∈(0,δ),使得

clcone(M-y0)∩-cl(Sε(Θ))={0},

则y0∈M称为Henig有效点,记为y0∈He(M,Θ).

设F:X→2Y是集值映射,F的有效域、 图和上图分别定义为:

∀x∈X.

(1)

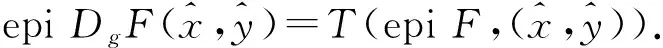
∀x∈X.

定义5[12]设向量函数η:X×X→X,S是不变凸的,F:S→2Y为集值映射.如果∀x1,x2∈S,∀λ∈(0,1),有

λF(x1)+(1-λ)F(x2)⊂F(x2+λη(x1,x2))+C,

则称F在S上关于η是C-预不变凸的.

2 Henig有效元的二阶最优性条件

考虑集值优化问题(P):

其中:S是X的非空子集;F:S→2Y是集值映射.

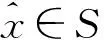
(2)

其中Cε0(Θ)=clcone(ε0B+Θ),B是Y中的闭单位球.

(3)

使得

(4)

(5)

由式(3),(4)知,存在N1∈,使得当n>N1时,

于是

∀n≥N1.

(6)

又由于λn→+∞,因此存在N2∈,使得当n>N2时,λn≥2,因而

∀n≥N2.

(7)

由式(6),(7)得vn∈-intCε(Θ)-C,∀n≥max{N1,N2},又由-intCε(Θ)-C⊂-intCε(Θ)得

vn∈-intCε(Θ), ∀n≥max{N1,N2}.

(8)

由式(5)知对任意的n≥max{N1,N2},存在K1(n)∈,使得

∀n≥max{N1,N2}, ∀k>K1(n),

于是

∀n≥max{N1,N2}, ∀k≥K1(n).

(9)

⊂-intCε(Θ)-C⊂-intCε(Θ),

Ø.

设

(10)

由引理2得0∉-intCε(Θ),于是y*≠0.由int cone(εB+Θ)⊂cone(εB+Θ)得

y*∈-cone(εB+Θ).

因此存在λ1≥0,z*∈-(εB+Θ),使得y*=λ1z*.由y*≠0得λ1>0,于是y*/λ1=z*,由-(εB+Θ)⊂-cone(εB+Θ)得y*/λ1∈-cone(εB+Θ),再由式(10)得

所以

引理4设S⊂X是不变凸的,F:S→2Y在S上关于η是C-预不变凸的,(x0,y0)∈graphF,由式(1)定义的G(η(x,x0))满足性质:

G(η(x,x0))⊂minG(η(x,x0))+C, ∀x∈S,

则对任意的(x,y)∈graphF,有

F(x)-y0⊂DgF(x0,y0)(η(x,x0))+C.

因而

下证(xn,yn)∈epiF.由于F在S上关于η是C-预不变凸的,于是

所以(xn,yn)∈epiF,从而(η(x,x0),y-y0)∈Tepi F(x0,y0),即

y-y0∈G(η(x,x0))={y∈Y: (η(x,x0),y)∈T(epiF,(x0,y0))}.

由引理中条件,类似文献[8]中命题2.4(i)的证明得

y-y0⊂DgF(x0,y0)(η(x,x0))+C,

于是

F(x)-y0⊂DgF(x0,y0)(η(x,x0))+C.

满足

并存在ε0∈(0,δ),使得

(11)

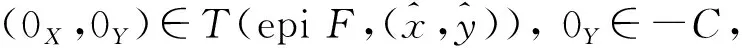
及定义3、 定义4和式(11)得

(12)

由F关于η是C-预不变凸的及引理4得

于是

(13)

下证

Ø, ∀x∈S.

(14)

z1+c1∈-int clcone(ε0B+Θ),

则

z1∈-c1-int clcone(ε0B+Θ)⊂-(C+int clcone(ε0B+Θ)).

由C=coneΘ得C⊂clcone(ε0B+Θ),于是

C+int clcone(ε0B+Θ)⊂int clcone(ε0B+Θ).

所以z1∈-int clcone(ε0B+Θ),从而

Ø,

这与式(12)矛盾.又由式(13),(14)得

Ø, ∀x∈S,

于是

Ø,

因此

Ø.

(15)

取ε1=ε0/2,则由引理2得

[-clcone(ε1B+Θ)]{0Y}⊂-int clcone(ε0B+Θ).

再由式(15)得

[1] Henig M I.Proper Efficiency with Respect to Cones [J].Journal of Optimization Theory and Applications,1982,36(3): 387-407.

[2] Borwein J M,Zhuang D.Super Efficiency in Vector Optimization [J].Transactions of the American Mathematical Society,1993,338(1): 105-122.

[3] Zheng X Y.Proper Efficiency in Locally Convex Topological Vector Spaces [J].Journal of Optimization Theory and Applications,1997,94(2): 469-486.

[4] QIU Qiu-sheng.On Henig Proper Efficiency [J].Journal of Systems Science and Mathematical Sciences,2011,31(4): 482-488.(仇秋生.关于Henig真有效性 [J].系统科学与数学,2011,31(4)：482-488.)

[5] YU Guo-lin,LIU San-yang.The Henig Efficient Subdifferential of Set-Valued Mapping and Stability [J].Acta Mathematic Scientia,2008,28A(3): 438-446.(余国林,刘三阳.集值映射的Henig有效次微分及其稳定性 [J].数学物理学报,2008,28A(3)：438-446.)

[6] CHEN Guang-ya,Jahn J.Optimality Conditions for Set-Valued Optimization Problems [J].Mathematical Methods of Operations Research,1998,48(2): 187-200.

[7] Jahn J,Khan A A,Zeilinger P.Second-Order Optimality Conditions in Set Optimization [J].Journal of Optimization Theory and Applications,2005,125(2): 331-347.

[8] LI Sheng-jie,Zhu S K,Teo K L.New Generalized Second-Order Contingent Epiderivatives and Set-Valued Optimization Problems [J].Journal of Optimization Theory and Applications,2012,152: 587-604.

[9] XU Yi-hong,XIAO Ming-li.The Super Efficient Generalized Gradiant of Set-Valued Map [J].Journal of Nanchang University: Engineering &Technology,2008,30(2): 127-130.(徐义红,肖明丽.集值映射的超有效广义梯度 [J].南昌大学学报: 工科版,2008,30(2)：127-130.)

[10] LI Zhong-fei,WANG Shou-yang.Connectedness of Super Efficient Sets in Vector Optimization of Set-Valued Maps [J].Mathematical Methods of Operations Research,1998,48(2): 207-217.

[11] Aubin J P,Frankowska H.Set-Valued Analysis [M].Basel: Birkhauser,1990.

[12] SHENG Bao-huai,LIU San-yang.Kuhn-Tucker Condition and the Wolfe Duality of Preinvex Set-Valued Optimization [J].Applied Mathematics and Mechanics: English Edition,2006,27(12): 1655-1664.