一类非线性波方程时间周期解的存在性
赵 昕
(吉林农业大学 信息技术学院,长春 130118)
考虑如下问题:
(1)
其中f是连续函数并且关于t是2π-周期的.
Rabinowitz[1]首先应用变分法,在非线性项满足超线性增长且严格单调的条件下,证明了波方程(1)非平凡时间周期解的存在性,之后,文献[2-6]进一步探讨了非线性波方程(1)时间周期解的存在性与多重性.为了研究非线性波方程的时间周期解,通常要求f单调[1-2].Coron[7]通过引入对称子空间,避免了波算子无穷维核空间所导致的紧性缺失,将问题转化为在子空间上研究波方程的周期解,从而在非线性项非单调且满足超二次条件下,得到了自治波方程的非平凡解.文献[5]应用Coron的技巧,在非线性项超线性增长且满足非二次条件时得到了问题(1)非平凡时间周期解的存在性.文献[4]应用该技巧得到了在非线性项满足渐近线性增长时问题(1)非平凡时间周期解的存在性.本文应用该技巧在非线性项满足超线性增长条件下研究问题(1),并且在超二次条件和非二次条件可能不满足[8]时研究问题(1)在非单调条件下非平凡时间解的存在性.
假设:
(H1)f∈C([0,2π]×[0,π]×,);
(H2) 存在p>2和a1,a2>0,使得
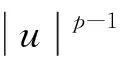
(H3) 当|u|→0时,f(t,x,u)=o(|u|)关于(t,x)∈Q一致成立;
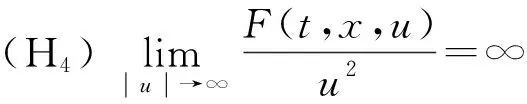
(H5) 存在常数C0>0,使得
H(t,x,u)≐uf(t,x,u)-2F(t,x,u)≤H(t,x,v)+C0,
其中0 (H6)f(t,x,u)=f(π+t,π-x,u),∀(t,x,u)∈Q×. 定义‖·‖r为空间Lr(Q)(r∈[1,∞))中的范数,(·,·)r为相应的内积.设空间 其范数为 其中 易见,E是自反Banach空间.令 定义函数Φ:E→, (2) 由假设条件(H1),(H2)可知,Φ∈C1(E,)且Φ为强不定泛函.易知问题(1)的一个弱解对应于Φ的一个临界点.因为E0是无穷维的,故可用Coron技巧把泛函Φ限定在一个合适的子空间X,使得X∩Ker□={0}.实际上,设 X={u∈E:u(t,x)=u(π+t,π-x)}, 记X+=X∩E+,X-=X∩E-,则有X=X-⊕X+,并且X在范数‖·‖X≐‖·‖E定义下是Banach空间.记‖u‖X为‖·‖,只需寻找Φ在X中的临界点即可.按照重数重新排列□的特征值为 …≤λ-,3≤λ-,2≤λ-,1<0<λ+,1≤λ+,2≤λ+,3≤…, 分别记φi(ej)为对应于λ+,i(λ-,j)的特征函数,则 在定理1的条件下, 类似于文献[5]的证明, 可得下列3个引理, 即Φ具有环绕结构并满足(C)c条件. 引理1若条件(H1)~(H3)成立,则存在ρ>0,使得 κ≐infΦ(∂Bρ∩X+)>0, (3) 其中Bρ≐{u∈X: ‖u‖≤ρ}. 引理2假设条件(H1)~(H6)成立,则存在R>0,使得 supΦ(∂Γ)≤0, (4) 其中 Γ≐{u=u-+sφ1:u-∈X-,s≥0,‖u‖≤R}, 且‖φ1‖2=1. 引理3假设条件(H1)~(H6)成立,则泛函Φ满足(C)c条件. 定理1假设条件(H1)~(H6)成立,则问题(1)至少存在一个非平凡弱解. 证明: 由条件(H1)~(H3),(H5),可得F(t,x,u)≥0,并且对于任意的u∈X,Ψ(u)≥0.于是根据f的增长性和X紧嵌入到Lr(Q)(r∈[1,∞))易知,Ψ弱下半连续且Ψ′弱连续.又由引理1和引理2可知,存在泛函Φ的(C)c序列{un},使得c≥κ>0.再利用引理3可知,序列{un}在X中一致有界,且存在u0∈X,使得在X中un→u0,从而Φ(u0)=c>0,且 ∀φ∈X. 因此,u0是问题(1)的一个非平凡弱解. [1] Rabinowitz P H.Free Vibrations for a Semilinear Wave Equation [J].Comm Pure Appl Math,1978,31(1): 31-68. [2] Brézis H,Coron J M,Nirenberg L.Free Vibrations for a Nonlinear Wave Equation and a Theorem of P.Rabinowitz [J].Comm Pure Appl Math,1980,33(5): 667-684. [3] Castro A,Preskill B.Existence of Solutions for a Semilinear Wave Equation with Non-monotone Nonlinearity [J].Discrete Contin Dyn Syst,2010,28(2): 649-658. [4] CHANG Xiao-jun,LU Jing-jing.Nontrivial Time-Periodic Solutions of a Class of Asymptotically Linear Wave Equations [J].Journal of Jilin University: Science Edition,2013,51(3): 373-376.(常小军,路京京.一类渐近线性波方程的非平凡时间周期解 [J].吉林大学学报:理学版,2013,51(3): 373-376.) [5] Costa D G,Magalhães C A.A Unified Approach to a Class of Strongly Indefinite Functionals [J].J Differential Equations,1996,125(2): 521-547. [6] JI Shu-guan,LI Yong.Time Periodic Solutions to the One-Dimensional Nonlinear Wave Equation [J].Arch Ration Mech Anal,2011,199: 435-451. [7] Coron J M.Periodic Solutions of a Nonlinear Wave Equation without Assumption of Monotonicity [J].Math Ann,1983,262: 273-285. [8] WEI Yuan-hong,CHANG Xiao-jun,LÜ Yue,et al.Superlinear Fourth-Order Elliptic Problem without Ambrosetti and Rabinowitz Growth Condition [J].Commun Math Res,2013,29(1): 23-31.