非凸情况下发展包含的反周期问题
王俊彦,高顺川,王春红
(1.长春工业大学人文信息学院 数学教研部,长春 130122;2.空军航空大学 基础部,长春 130022;3.吉林大学 数学研究所,长春 130012)
关于发展包含的反周期问题目前已有许多研究结果[1-6].本文在文献[6]的基础上考虑更一般情况下,当集值函数取非凸值时发展包含解的存在性.
设H是可分的Hilbert空间,V是H的稠子集,具有自反可分的Banach空间结构,且连续地紧嵌入H.等同H及其对偶,有V→H→V*,所有嵌入都是连续的、 稠的.三元组(V,H,V*)称为“发展三元组”.设I=[0,b]是一个闭区间.记X表示Lp(I,V),X*表示Lq(I,V*),其中p>1,1/p+1/q=1;‖·‖X表示X中的范数;(·,·)表示空间H的内积;〈·,·〉表示(V,V*)中的对偶对;《·,·》表示(X,X*)中的对偶对;Pk(R)表示实数集所有非空紧子集的全体.
考虑如下发展包含的反周期边值问题:
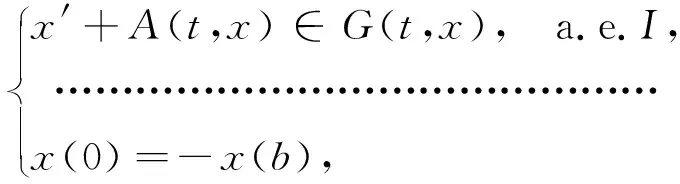
(1)
其中:A:I×V→V*是一个非线性半连续算子;映射G:I×H→2V*{Ø}是一个集值映射.考虑方程(1)在G(t,x)为非凸值情况下解的存在性.假设:


不失一般性,对于所有的t∈I,设A(t,0)=0;H(F):G:I×H→Pk(V*)是一个集值映射,满足:
1) (t,x)→G(t,x)是图像可测的;
2) 对几乎所有的t∈I,都有x→G(t,x)是下半连续的;

定理1若假设(H1)~(H3)及H(F)成立,则问题(1)至少存在一个解x∈Wpq(I),且解集是一致有界的.
证明: 设N:Lp(I,H)→2Lq(I,V*)为集值映射G的Nemitsky算子,定义如下:
N(x)={v∈Lq(I,V*):v(t)∈G(t,x(t))} a.e.I.

为证明x→d(w,N(x))是上半连续的,只需证明对任意的λ≥0,水平集Uλ={x∈Lq(I,V*):d(w,N(x))≥λ}在Lq(I,V*)中是闭的.设{xn}n≥1⊆Uλ并假设在Lq(I,V*)中xn→x,则存在子列,不妨设其为xn→xa.e.于I.由1)知,x→d(w,F(t,x))为一个上半连续+函数.因此,由Fatou引理,有
于是x∈Uλ,进而可知N(·)是下半连续的.根据连续选择定理知,存在连续函数f:Lp(I,H)→Lq(I,V*),使得f(x)∈N(x).

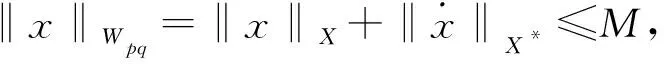
因此,原问题求解可转化为该方程的不动点问题:x=L-1∘f(x).由f的连续性,可知L-1∘f:Lp(I,H)→Lp(I,H)是紧算子.下面证明集合
Γ={x∈Lp(I,H):x=σL-1∘f(x),σ∈(0,1)}
是有界集.设x∈Γ,则有

由2)得
(2)
两边积分得

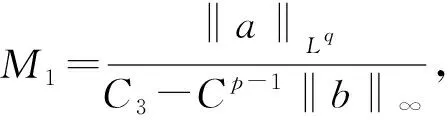
因此,Γ在Wpq中是有界集.又由于Wpq(I)→Lp(I,H)是连续嵌入的,故Γ在Lp(I,H)中是有界集.根据Leray-Shauder定理可知,存在一个x∈Wpq(I),使得x=L-1∘f(x),即x为问题(1)的解.
[1] Okochi H.On the Existence of Anti-periodic Solutions to a Nonlinear Evolution Equation Associated with Odd Subdifferential Operators [J].J Funct Anal,1990,91(2): 246-258.
[2] LIU Qing.Existence of Anti-periodic Mild Solutions for Semilinear Evolution Equations [J].J Math Anal Appl,2011,377(1): 110-120.
[3] WANG Yan.Antiperiodic Solutions for Dissipative Evolution Equations [J].Math Comput Modelling,2010,51: 715-721.
[4] CHEN Yu-qing,WANG Xiang-dong,XU Hai-xiang.Anti-periodic Solutions for Semilinear Evolution Equations [J].J Math Anal Appl,2002,273(2): 627-636.
[5] CHEN Yu-qing,Nieto J J,O’Regan D.Anti-periodic Solutions for Evolution Equations Associated with Maximal Monotone Mappings [J].Applied Mathematics Letters,2011,24(3): 302-307.
[6] ZHANG Yu-mei,CHENG Yi,WANG Jing-hua.Anti-periodic Boundary Value Problem for a Class of Evolution Equation in Banach Space [J].Journal of Jilin University: Science Edition,2012,50(4): 715-716.(张育梅,程毅,王靖华.Banach空间中发展方程的反周期边值问题 [J].吉林大学学报: 理学版,2012,50(4): 715-716.)
[7] Zeidler E.Nonlinear Functional Analysis and Its Applications: Ⅰ.Fixed-Point Theorems [M].Berlin: Springer-Verlag,1984.
[8] Zeidler E.Nonlinear Functional Analysis and Its Applications: Ⅱ.Linear Monotone Operators [M].New York: Springer-Verlag,1990.

