区域性椭球元素确定方法的比较
尹伟言,赵 鑫
(1.国家测绘局第一大地测量队,陕西 西安 710054;2.国家测绘局测绘标准化研究所,陕西 西安 710054)
在城市独立坐标系建立过程中有一个重要的问题就是区域性椭球元素的确定。因为在坐标归算过程中,地面—椭球面—平面,需要一椭球作为过渡,而选择与边长归算高程基准面(以下简称为投影面)最佳密切吻合的椭球就称为区域性椭球,这样可以在一定程度上减小边长的投影长度变形。确定区域性椭球有很多方法,主要有单点法、多点法、定向定位调整法。文献[1-3]从理论上对上述方法做了大量研究,本文主要侧重于实际数据的比较与分析,并得出了一些较有意义的结论。
1 椭球变换方法
1.1 广义大地坐标微分方程
由于椭球的定向和定位的不同,椭球参数的变化,以及两坐标系统尺度上的差异,使得大地坐标发生了变化,常采用广义大地坐标微分公式[4]表示为
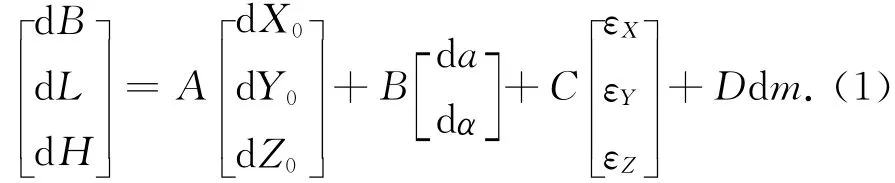
式中:[dX0,dY0,dZ0]T为坐标原点的平移量,[da,dα]T为椭球参数变化量,[εX,εY,εZ]T为坐标轴旋转参数,dm为新旧坐标系尺度比,系数A,B,C,D的表达式参见文献[5]。
1.2 单点法
使区域性椭球面和测区投影面仅在单个位置基准点上相合的方法,称为区域性椭球的单点法[6]。如图1所示。
图1中,P0(B0,L0,H0)是位置基准点,H是投影面的大地高,ζ为高程异常,对于整个测区一般取同一个概略值。设国家参考椭球为E0椭球,所求得的区域性椭球为Ei椭球。

图1 投影面与区域性椭球面
单点法包括椭球膨胀法、椭球平移法和椭球变形法。具体的理论推导在文献[6]中已详细给出,这里仅归纳这几种方法确定出的区域椭球元素以及大地坐标变动量公式。
1.2.1 椭球膨胀法
椭球膨胀法只改变椭球的长半径a,不改变椭球的扁率。那么由式(1)可得

1)由基准点上国家参考椭球平均曲率半径变动量反求椭球长半径的变动量[1],这样所得到的区域性椭球称为E1椭球。任意一点大地坐标的变动量为

从式(3)可以发现E1椭球在位置基准点处并不与投影面完全贴合。
2)以基准点上国家参考椭球面与投影面之间的垂向距离H作为长半径变动量,这样所得到的区域性椭球称为E2椭球。任意一点大地坐标的变动量为

从式(4)可以看出,E2椭球在位置基准点处与投影面不是完全贴合的,而且除赤道(Bi=0)外,所确定出的E2椭球面必低于投影面。
1.2.2 椭球平移法
椭球平移法就是仅改变E0椭球的中心位置并不改变其定向和椭球元素。这样所确定的区域椭球称为E3椭球。那么由式(1)可得

采用E0椭球元素,将E0椭球沿着位置基准点P0的法线方向平移H,并保持基准点在E0椭球上的大地经纬度不变,这样使E3椭球面与投影面在基准点处重合。那么,基准点P0处的大地高变动量为-H,任意一点大地坐标的变动量为
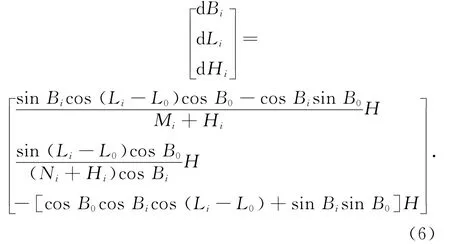
在位置基准点处[dB0,dL0,dH0]T=[0,0,-H]T,即E3椭球面与投影面在基准点处重合,但是其余点的大地经度发生了较大的变化。
1.2.3 椭球变形法
椭球变形法是同时改变E0椭球的长半径和第一偏心率,这样所确定的区域性椭球称为E4椭球。那么由式(1)和e2=2a-a2可得

不改变E0椭球的定位和定向,将位置基准点P0的大地高H0变为H′0,同时改变椭球的长半径和扁率,以保证P0处两椭球的法线方向重合以及三维直角坐标不变。任意一点大地坐标的变动量为

在位置基准点处[dB0,dL0,dH0]T=[0,0,-H]T,E4椭球面与投影面在基准点处重合,由于椭球定位定向没有改变,所以其它点的经纬度变动量相对小一些。
1.3 多点法
使区域性椭球面与边长归算投影面在整个测区或城市范围内的多个网点上都更加相合的方法,称为多点法[6]。所得到的椭球称为E5椭球。
首先在E4椭球元素的基础上,求得各点基于E4椭球的(Bi,Li,Hi)。在测区中央及周围选取m个实施了水准测量的GPS点,其水准高程为hi(i=1,2,…,m)。再变动E4椭球的长半径和第一偏心率,使得椭球面和这m个点更加密切吻合,由式(8)可以得到大地高的变动量为

经过椭球元素变动后,在这m个点上椭球面与投影面之间的偏差

式中:B=[-Wi,Nisin2Bi/2],X=[da,de2]T,l=hi-Δh-Hi。
最后得到由多点法所确定出的区域椭球元素为
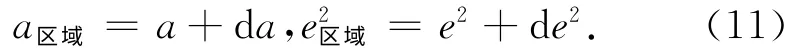
式中,a和e2是E4椭球元素。
通过多点法确定的区域性椭球,在测区范围内使两个面的偏离程度进一步减小,与投影面吻合的更好。
1.4 定向定位调整法
定向定位调整法旨在消除两个面之间的倾斜,是通过在位置基准点处绕地平正北和正东方向的旋转,使得椭球面的法线方向趋于垂线方向[2]。这样所确定出来的椭球称为E6椭球。
首先,在E4椭球元素的基础上,求得各点基于E4椭球的(Bi,Li,Hi)。在P0点上,E4椭球面的法线方向与垂线方向并不一致,其夹角为垂线偏差μ,可分解为子午分量ζ和卯酉分量η。文献[2]推导出了旋转角的垂线偏差分量与大地高变动量之间的关系式,为了节约篇幅,这里不再列出具体推导过程,仅给出结果表达式。
大地高的变动量与垂线偏差分量之间的关系为
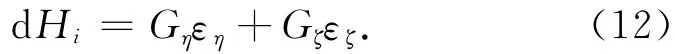
式中:。
为了求定垂线偏差,可采用类似于上节中的多点法,利用测区中央及周围的m个实施了水准测量的GPS点,求得E4椭球面与投影面之间的偏差,以式(12)为函数模型,按最小二乘估计求垂线偏差的两分量。
确定出垂线偏差后,利用文献[2]中的式(12)~(14)以及E4椭球元素,可以得到在E6下的大地坐标。
利用定向定位法所确定出的椭球面,不仅考虑了位置基准点处椭球面与投影面之间的垂向偏离,还进一步顾及了两个面之间的倾斜,这样使得在整个测区范围内,区域椭球面与投影面更加密切吻合[1]。
2 数据验证
文献[1,3]已对单点法和多点法进行了数据验证的比较分析,所得结论是:与单点法相比,整个测区按多点法确定的区域椭球面更吻合于投影面。而在本文中,笔者将利用实测数据对多点法确定的E5椭球和定向定位调整法确定的E6椭球进行比较与分析。
本次的实验数据来自某市B级GPS控制网成果,共135个点,均匀分布整个市,如图2所示。

图2 GPS点位分布图
在测区中央选取一个基准点P0=(31°25′38.851 20″,120°44′45.660 33″,12.862m),P0正常高为3.771m,那么P0处高程异常值为9.091m。投影面的大地高H=-48.033m,由P0的大地坐标,通过式(11)和式(12)可以算出E4椭球元素为

在E4椭球的基础上,按照多点法确定出E5椭球元素,根据式(14)和式(15)解算出E5椭球元素相对于E4椭球元素的增量为

在E4椭球的基础上,按照定向定位调整法确定出E6椭球,E6椭球与E4椭球具有相同的椭球元素,区别是定向定位不同。根据式(16)解算出垂线偏差两个分量为

确定E5和E6椭球的最终目的均为:使得在整个测区范围内,区域椭球面与投影面更加密切吻合。表1列出其中10个点分别基于E5椭球和E6椭球下投影面与椭球面之间的距离。

表1 E5和E6椭球面与投影面之间的距离(10为基准点P0) m
图3更加直观形象地表示出135个GPS网点的E5和E6椭球面与投影面之间的距离。

图3 E5和E6椭球面与投影面之间的距离
根据计算的数据和图3可以发现:
1)E5椭球面与投影面之间的距离最大为2.088m,最小为0.019m,在位置基准点处距离为0.166m,投影面与椭球面之间的距离偏大,平均在分米级;
2)E6椭球面与投影面之间的距离最大为0.216m,最小为0m,在位置基准点处距离为0m,投影面和椭球面之间的距离普遍很小,平均在厘米级;
3)通过比较E5和E6椭球,可以得出这样的结论:采用定向定位调整法确定的E6椭球面与投影面更加密切吻合,优于采用多点法确定的E5椭球面。
3 结 论
1)本文介绍了目前常用的3种椭球变换理论与方法,对各种方法的特点进行分析,归纳了E1-E6椭球元素及大地坐标变动量的公式,方便各类工程的使用。
2)利用某市B级GPS控制网数据对多点法确定的E5椭球和定向定位调整法确定的E6椭球进行比较与分析,从表1和图3中可以发现E6椭球面与投影面更加密切吻合,优于E5椭球。
3)对于面积较小的测区而言,可以采用单点法确定区域椭球;但是对于大面积测区,离基准点越远,椭球面与投影面之间的倾斜越严重,因此,建议采用E6椭球作为区域椭球。
[1]施一民.单点和多点法确定区域性椭球空间位置及元素[J].同济大学学报,2004,32(5):648-651.
[2]施一民,周拥军.用定向定位调整法确定区域性椭球面[J].测绘学报,2002,31(2):118-122.
[3]施一民,张文卿.区域性椭球元素的最佳确定[J].测绘工程,2000,9(3):27-29.
[4]畅开狮.建立城市独立坐标系相关问题的探讨[J].城市勘测,2008(1):86-90.
[5]孔祥元.控制测量学(下册)[M].武汉:武汉大学出版社,2010:166-178.
[6]施一民.现代大地控制测量[M].北京:测绘出版社,2008:218-228.
[7]丁士俊,畅开狮,高顺义.独立网椭球变换与坐标转换的研究[J].测绘通报,2008(8):4-6.
[8]李世安,刘经南,施闯.应用GPS建立区域独立坐标系中椭球变换的研究[J].武汉大学学报:信息科学版,2005,30(10):888-891.

