一类乘积形式的差分不等式

卢钰松

(河池学院数学与统计学院，广西宜州546300)

0 引言

由于Gronwall-Bellman型积分不等式的离散形式的推广形式是研究差分方程解的存在性、唯一性、有界性，对初始条件和参数的连续依赖性、稳定性等定性性质的重要工具，人们不断地对它的形式进行各种推广，使它的应用范围不断的扩大(例如文献［1-6］及其引文)。其中，Pachpatte对Gronwall-Bellman型积分不等式作了深入研究，得出以下结论。

引理1［1，4］假设对于任意自然数n和非负实数r，函数w(n，r)是连续的实值函数，且对于任意给定的n，w(n，r)关于r是单调不减的。如果函数u(n)满足不等式

又假设r(n)是差分方程

的最大解，而且有u(0)≤r(0).则有

引理2［3］假设u0是非负常数，a(s)，b(s)，h(s)是定义在自然数集0上的非负函数，如果函数u(n)满足不等式

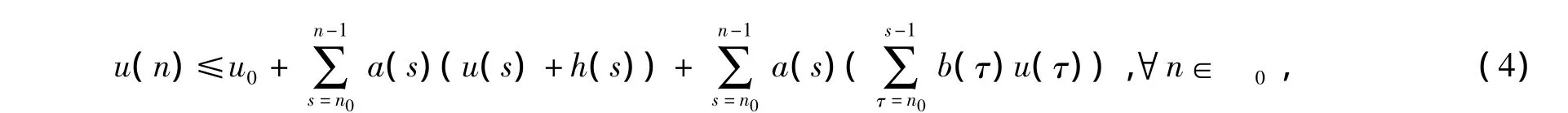
则有

引理3［5］假设c是非负常数，a(s)，b(s)是定义在自然数集0上的非负函数;假设对于任意自数n和非负实数r，函数w(n，r)是非负实函数，且对于任意给定的n，w(n，r)关于r是单调不减的。如果函数u(n)满足不等式

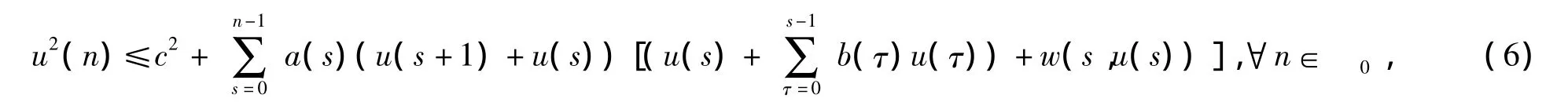
那么

其中

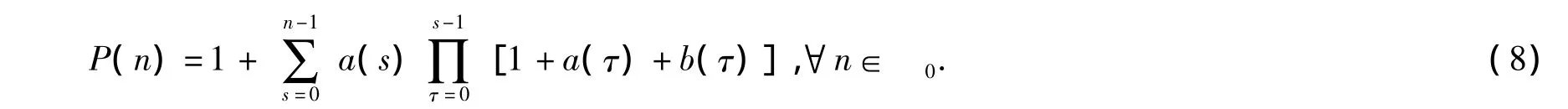
r(n)是差分方程

的解。

本文在文献［4-5］的基础上，研究下面的差分不等式

给出未知函数的估计，综合运用文献［4-5］的方法进行严格的证明。

1 主要结果及其证明

在本文中，0={0，1，2，…}，T={1，2，…，T}，T∈0， RR+∶=［0，∞)，C(A，B)表示A到B的连续函数全体。函数z(n)的差分，记为Δz=z(n+1)-z(n).显然，具有初始条件x(0)=0的线性差分方程Δx(n)=b(n)有解x(n)=b(s).为叙述方便，我们补充规定b(s)=0.

定理1假设函数m(s)是定义在自然数集0上非负的单调不减函数，a(s)，b(s)，h(s)是定义在自然数集0上的非负函数，如果函数u(n)满足不等式

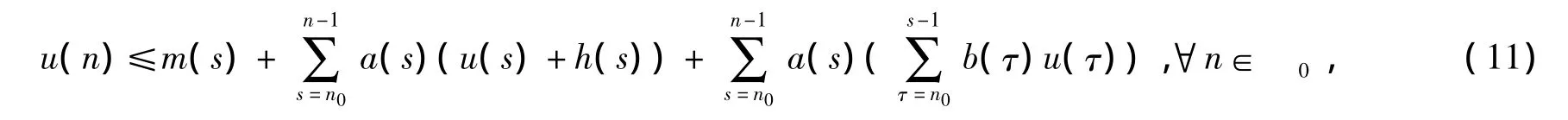
则有

其中

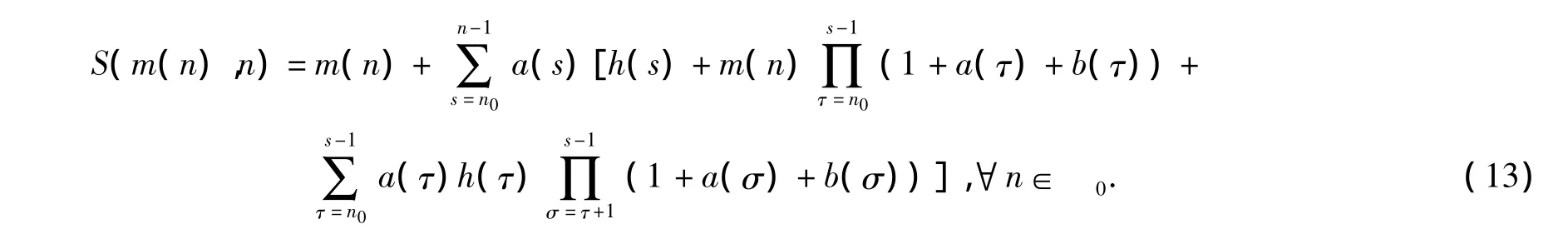
证明:任意取定一个自然数T，因为m(t)是单调不减函数，由式(11)可以推出

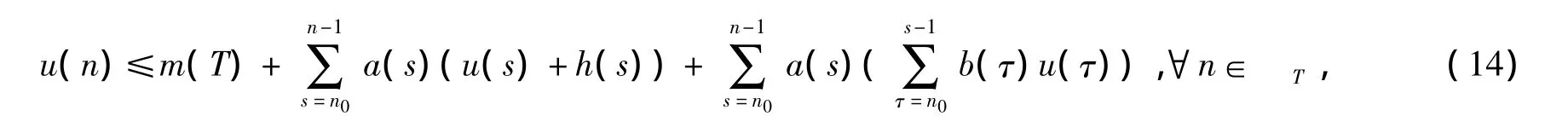
根据引理2，不等式(14)中的未知函数有估计式

由T的任意性得到定理1的估计式(12)。

定理2假设c是非负常数，a(s)，b(s)，h(s)是定义在自然数集0上的非负函数;假设对于任意自然数n和非负实数r，函数w(n，r)是非负连续实函数，且对于任意给定的自然数n，函数w(n，r)关于r是单调不减的。如果函数u(n)满足不等式(10)，则有

其中函数S由式(13)定义，函数v(n)是差分方程

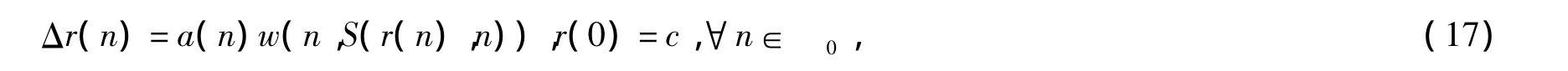
的最大解。

证明:首先假设c是正常数。定义函数z(n)等于式(10)的右端，则z(n)是0上的不减正函数且有

根据函数z的定义和差分的定义，对任意n∈0，我们有

由差分定义和式(19)，对任意自然数n我们可以得到

在式(20)中先把n替换成s，然后在分别令s=0，1，2，…，n-1，这将得到n个不等式，最后把所得不等式两边分别相加得到

用下式定义函数z1(n)

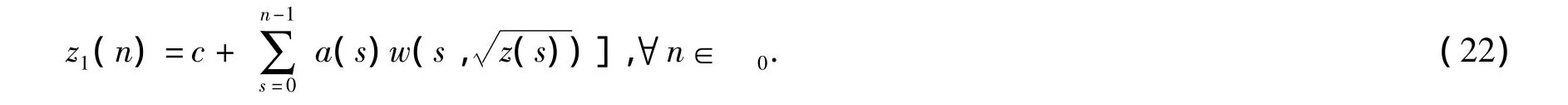
易知z1(n)是0上的正的单调不减函数，且z1(0)=c.

由z1(n)的定义及差分的定义可得

另一方面，由式(21)和式(22)，可以得出

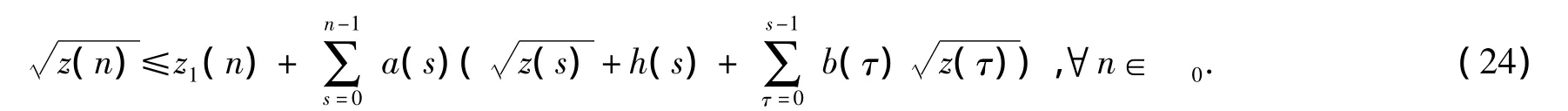
因为z1(n)是正的单调不减函数，a(s)，b(s)，h(s)是定义在自然数集0上的非负函数，所以满足定理1中的条件，我们利用定理1，得到式(24)中函数的估计式

其中S(n)由式(13)定义.把式(25)代入式(23)，根据w的单调性我们得到

由式(13)可得S(z1，n)关于z1是连续单调增函数，又因为w(n，r)关于r是连续的单调不减函数，推出式(26)右端关于z1是连续单调不减函数。利用文献［1-4］中的比较原理，即引理1，我们可以推出

式(27)中v(n)是差分方程(17)的最大解.由式(18)，(25)和(27)，我们得出所要证明的估计式(16)，即

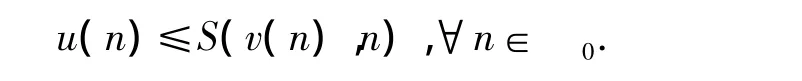
如果c是非负常数，我们用c+ε代替c重复上面的证明过程，其中ε＞0是任意小的常数。然后令ε→0，对所得结果求极限同样得到所要证明的估计式(16)。

［1］ B G Pachpatte.Finite dierence inequalities and an extension of Lyapunovs method［J］.Michigan Math.J.，1971，18:385-391.

［2］ B G Pachpatte.On some new discrete inequalities and their applications［J］.Proc.Nat.Acad.Sci.India，1976，46:255-262.

［3］ B G Pachpatte.Finite-difference inequalities and discrete-time control systems［J］.Indian J.Pure.Appl.Math.，1978，9:1 282-1 290.

［4］ B G Pachpatte.Comparison theorems related to a certain inequality used in the theory of differential equations［J］.Soochow J.Math.，1996，22:383-394.

［5］ B G Pachpatte.Inequalities applicable in the theory of finite difference equations［J］.J.Math.Anal.Appl.，1998，222:438-459.

［6］ 王五生，李自尊.一类新的非线性和差分不等式及其应用［J］.系统科学与数学，2012，32(2):181-189.