压缩感知理论下扩展迭代重加权最小二乘算法的性能分析*

陈小玲，赵慧民，魏文国

(广东技术师范学院电子与信息学院，广东 广州 510665)

基于几何影射学原理，经典的压缩感知理论可以表示为：

mincard(x)s.t.A(X)=b

(1)

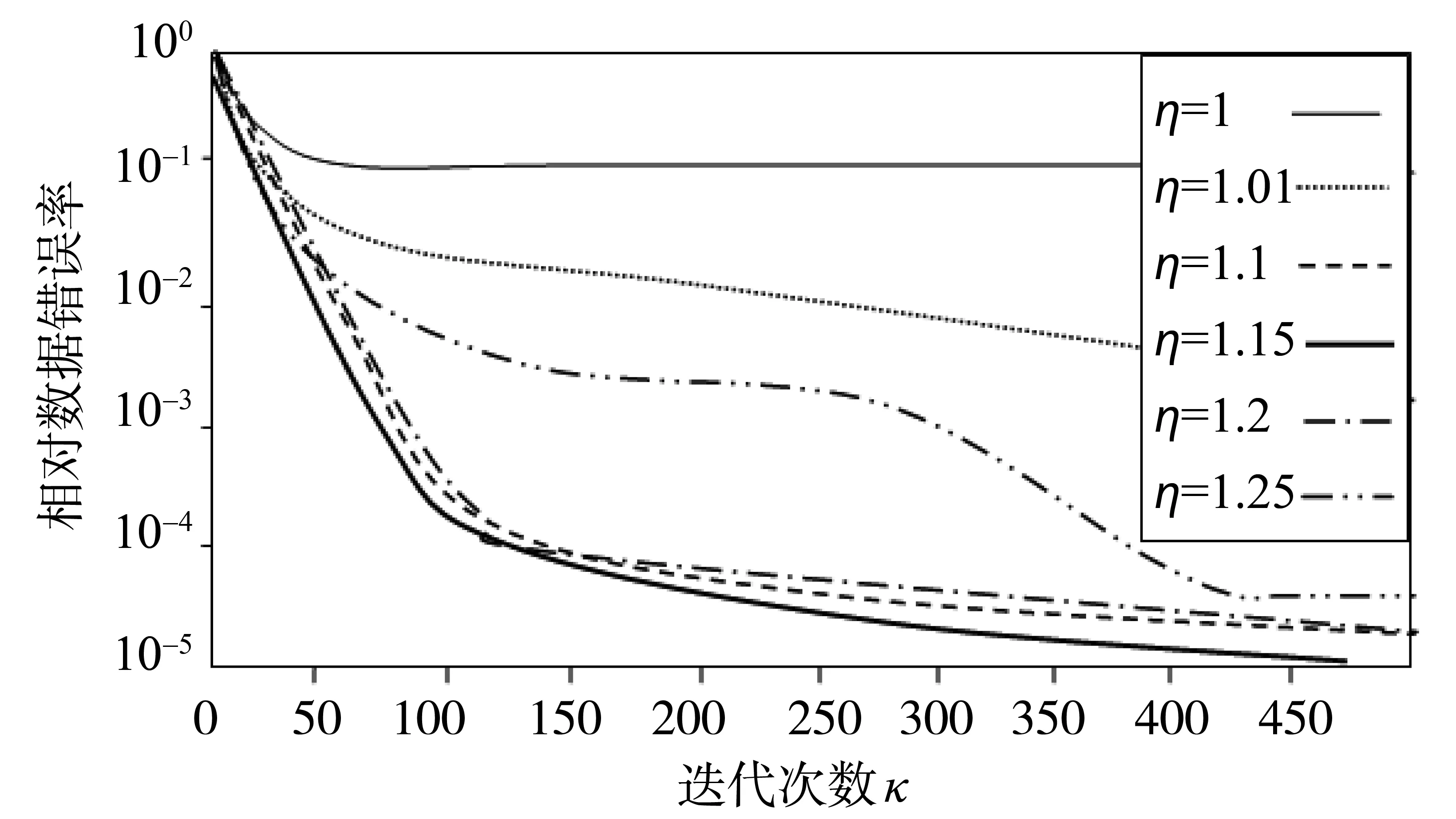
这里x∈Rn,A∈Rm×n，card(x)表示张成希尔伯特空间x的非零元素集，X是x的全体。目前，解决(1)式的几种主要算法是基于最小l1范数的凸优化算法、匹配追踪等贪婪算法[1 - 5]。为了改进最小l1范数算法的信号恢复性能，Candes和Daubechies等[6-7]分别提出了迭代重加权l1和迭代重加权最小二乘IRLS-p(0

(2)

Chartrand等[9 - 10]证明，在A的零空间假设条件下，核范数最小化IRLS-1算法的输出与最低秩A(X)=b的结果是一致的。同时，他说明在p<1时IRLS-p比最小l1范数具有更好的信号恢复性能。基于此条件，利用几何影射学原理[11]，通过每次迭代时对加权F范数(即Frobenius Norm)的最小化处理，本文分析了一类扩展EIRLS-p算法的性能。在此基础上，通过梯度投影GP(Gradient Projection)简化迭代二乘目标函数的求解过程，进而实现了一类短时迭代重加权最小二乘算法(简称sEIRLS-p算法)。本文研究的目的是，实现压缩感知理论下EIRLS-p算法的收敛性与实时性之间的有效折中，为信号高质量恢复提供一种新的研究参考。

1 几何影射EIRLS-p算法

定义矩阵X的核范数为‖X‖*=∑iσi(X)，其中σi(X)代表了X中第i个最大奇异值。由此，对于求解压缩感知理论的(1)式问题，我们可以得到一种最小核范数关系式：

(3)

(3)式的求解类似于凸优化最小l1范数算法，但凸优算法的最大问题是迭代收敛性能较差[13]。为此，我们考虑(3)式的一种秩函数非凸优近似求解方法。定义F(Frobenius)范数下的一种平滑Schatten-p函数形式为

(4)

这里Tr(·)为矩阵的迹。由矩阵迹函数的性质可知，当p>0时，函数fp(X)是可微的；当p≥1时，fp(X)具有凸性；而满足γ=0∪p→0时，fp(X)→rank(X)。当p=1,γ=0时，f1(X)=‖X‖*称为Schatten-1范数。因此，对(3)式的求解近似于求解以下问题:

minfp(X)s.t.A(X)=b

(5)

注意到对(4)式取微分有:▽fp(X)=pX(XTX+γ·I)p/2-1。代入(5)式，则其成立的一种KKT方程条件(Karush-Kuhn-Tucker最优化条件)可写为[14]：

X(XTX+γ·I)p/2-1+A*(λ)=0

A(X)=b

(6)

其中，A*(λ)表示特征值为λ时矩阵A的共轭矩阵。对(6)式KKT条件1求解有：

(7)

(8)

由式(7)、(8)可见，Xk+1满足了(6)式的KKT条件，且遵循了(9)式的凸优化关系：

(9)

说明，秩最小化EIRLS-p系列算法就是对应压缩感知凸优化算法的一种近似扩展。

1.1 EIRLS-1实现的收敛性

为了准确分析EIRLS-1算法连续迭代收敛的特性，定义F范数意义下的一种函数：

γTr(W)+Tr(W-1))

(10)

其中Z∈G(b)，G(b)为零状态空间中A(X)=b的希尔伯特空间解集。当p=1时，EIRLS-p算法的第2步迭代等价于

Xk+1=argminZ∈G(b)Γ(Z,Wk,γk)

(11)

选择γk+1=min{γk,σK+1(XK+1)/N，其中K和N是固定整数。把(10)式加权矢量代入(11)，并根据矩阵迹和F范数的性质，我们可以同时得到以下迭代关系[14-16]:

(12)

且有关系

Γ(Xk+1,Wk+1,γk+1)≤Γ(Xk+1,Wk,γk+1)≤

Γ(Xk+1,Wk,γk)≤Γ(Xk,Wk,γk)

(13)

由此，对于任意k≥1，我们有关系‖Xk‖*≤Γ(X1,W0,γ0):=D。这里，W0=I,γ0=1。且存在σi(Wk)≥D-1,j=1,2,...,min[m,n]。这说明，在张成希尔伯特零状态空间内，通过选择一定的调节参数γ，EIRLS-1算法总能够有效收敛，且能够用具有唯一最小化秩的核范数矩阵表示[11，17]。

1.2 EIRLS-0实现的收敛性

为了说明EIRLS-0实现算法的收敛性,定义一种对于W和X都严格凸性的F范数函数:

Η(X,W,γ)=Tr(WXTX)+γ·TrW-logdetW

(14)

其中，detW表示矩阵W的行列式。根据矩阵迹和F范数的性质，类似于公式(13)存在如下关系:

H(Xk+1,Wk+1,γk+1)≤H(Xk+1,Wk,γk+1)≤

H(Xk+1,Wk,γk)≤

H(Xk,Wk,γk)

(15)

对于任意k≥1，我们有logdet(XkTXk)≤H(X1,W0,γ0):=E。设σj(Wk)为加权矩阵W第k次迭代的第j个奇异值，则存在有不等关系式σj(Wk)≥e-E,j=1,2,...,t.其中，t=min[m,n]。这也说明了EIRLS-0算法能够有效收敛，且能够用一种稳定的矩阵形式唯一表示。

2 基于梯度投影的sEIRLS-p算法

2.1 sEIRLS-p算法的实现原理

借鉴梯度投影对交替迭代优化求解的实现过程[18]，我们在构造低秩矩阵时，把矩阵X的实现问题也可通过梯度投影(GP)方式进行计算，并得到EIRLS-p算法实现的另一种形式-短时扩展迭代重加权最小二乘(sEIRLS-p)算法。其满足关系：

minrank(X)s.t.ΡΩ(X)=ΡΩ(X0)

(16)

这里，X0是我们要恢复的信号数据矩阵。ΡΩ：Rn×n→Rn×n，表示矩阵X在支撑Ω中投影时数据元素Xij的投影算子，(i,j)∈Ω。sEIRLS-p算法的实现过程描述如下：

设置k=0,X0=0，按以下步骤迭代计算：

3) 设置k=k+1。重复1)-3)直到收敛。

由此可见，对于固定的γ参数，sEIRLS-p(0

2.2 sEIRLS-p算法的快速梯度投影

在不同条件下，为了使EIRLS算法能够用低秩矩阵实现数据的高概率恢复，同时又能使系统满足实时性要求，我们用梯度投影关系ΡΩ(X)=ΡΩ(X0)替代EIRLS-p算法中A(X)=b的约束条件。同时，用梯度投影(GP)算法求解EIRLS算法中每次迭代的最小二乘运算过程。为此，我们得到一种快速sEIRLS-p算法的具体实现方式如下：

设置k=0,X0=0，按以下步骤迭代：

2) 设置梯度投影常数为L,进行梯度投影(GP)。

b)Xold=Xnew.返回a)迭代直到GP收敛。

3)Xk+1=Xnew,k=k+1，返回1)直到EIRLS-p算法收敛。

算法中，GP的步长为2/Lk，Lk是二次方函数Tr(WkXTX)在第k次迭代的利普希兹(Lipschitz) 梯度常数。由算法可见，GP算法是利用EIRLS算法第k次迭代的结果作为第(k+1)次迭代梯度投影的先验条件，然后寻找每次迭代加速收敛的一种实现过程。

3 算法的验证及其性能分析

3.1 算法验证的参数选择

设原始数据矩阵为X，由Y·YT产生，其中Y为I.I.D高斯分布的数据矩阵，且Y∈Rn×r，n=500。归一化要恢复的矩阵为X0(最大奇异值为1)，其大小为500×500。X0的秩r分别设置为5、10、15，同时，我们定义当算法恢复的信号数据相对错误率ξ=‖X-X0‖F/‖X0‖F≤10-3时，信号恢复是成功的。实验时，支撑Ω通过均值为q的贝努立{0,1}随机值产生。所做实验用Matlab在Intel双核处理器上执行，其CPU为3 GHz，RAM大小为3.25 GB。

图1 n=500，p=0, η=1.15,不同γc条件下EIRLS-p算法的实现性能Fig.1 n=500，p=0, η=1.15, implementation performances of EIRLS-p to different γc

由图1可见，当γc<10-3时，收敛速度较快，但相对错误率ξ值较大；而当γc>10-3时，相对错误率ξ较小，但收敛速度较慢。因此，γc的选择是影响EIRLS-p算法实现性能的关键。由验证实验结果可知，选择γc=10-3，EIRLS-p算法恢复数据的性能最好。

刻度参数η的选择：设置γc=10-3，定义秩为r的矩阵X0的自由度为r(2n-r)，矩阵X0的自由度率FR=r·(2n-r)/q,采样率SR=q/n2。通过实际计算过程可知，如果FR>0.4或接近于1，算法恢复矩阵X0就很困难；反之，如果FR<0.4或接近于0，则恢复X0就比较容易。

图2表示了EIRLS算法与刻度参数η的敏感性关系。算法实现时，当确定γ0后，η取决于X0的秩和SR的大小。对于不同条件的X0实现问题，我们随机产生10个支撑。由图可见， 如果X0的秩r=5、10、15，FR=0.18、0.2、0.33时，η=1.15、1.1、1.05，算法恢复数据的错误率都较低，其实现性能都较好。

图2 n=500，γc=10-3，不同η条件下EIRLS算法的实现性能Fig.2 n=500, γc=10-3,implementation performances of EIRLS to different η

3.2 算法的实验结果及其性能比较

算法实现时，我们认为当数据相对错误率ξ≤10-3时，表示算法成功恢复了原始信号，并用NS作为成功恢复的次数。实验时选择γc=10-3，同时，当FR<0.4时，选择η=1.1；而当FR≥0.4时，选择η=1.03。表1列出了当FR<0.4时，在相同实验参数设置下算法的实现性能，并与SVT算法进行了比较。可见，EIRLS-0,sEIRLS-0,EIRLS-1,sEIRLS-1算法都能够较好地恢复原始数据，但SVT在某些情况下却是无效的。由表也可以看到，EIRLS-0比EIRLS-1算法收敛时需要更少的迭代次数和更低的计算时间。而在各种情况下，sEIRLS-0算法具有最好的实时性能。

表1 EIRLS和SVT算法的实现性能比较(FR<0.4)Table 1 Performances comparison for EIRLS and SVT algorithm (FR<0.4)

表2说明了当FR≥0.4时，算法sEIRLS-1、EIRLS-0、sEIRLS-0的实现性能。由表可见，在不同条件下，EIRLS-0、sEIRLS-0都能较好地恢复原始数据，但sEIRLS-1算法在某些情况下是无效的(SVT在各种条件下都不能执行，因此这种情况下没有列出)。当n>500后，相比其它算法，sEIRLS-0具有更好的实时性能。

由以上的结果可见，在sEIRLS-p、EIRLS-p系列算法中，sEIRLS-0实时性更强、实现性能最好。因此这里，我们主要比较sEIRLS-0和IHT算法的实现性能。在不同情况下，表3和4分别列举了两种算法实现时的需要的迭代次数、恢复次数NS以及计算时间。由表3可见，当FR<0.4时，两种算法具有一定的可比较性。而当FR≥0.4时，由表4可见，sEIRLS-0算法的实现性能明显优于IHT算法。

表2 EIRLS算法的实现性能分析(FR≥0.4)Table 2 Performances analyzing for EIRLS algorithm (FR≥0.4)

表3 sEIRLS-0和IHT算法的实现性能比较(当FR<0.4时)Table 3 Performances comparison for sEIRLS-0 and IHT algorithm (FR<0.4)

表4 sEIRLS-0和IHT算法的实现性能比较(FR≥0.4时)Table 4 Performances comparison for sEIRLS-0 and IHT (FR≥0.4)

4 总结与展望

基于几何影射求矩阵秩最小化问题，分析了EIRLS-p和sEIRLS-p的系列实现算法，并分析了它们在各种情况下的收敛性和实时性。在零状态空间及其假设条件下，EIRLS-1算法能够收敛到唯一核范数函数，这与最低秩矩阵满足几何影射的约束条件是一致的。我们也说明了EIRLS-0和sEIRLS-p算法收敛到最小平滑函数的稳定点问题，并给出了通过梯度投影实现算法的具体结构。在不同条件下的实验结果表明，EIRLS-0和sEIRLS-0算法比SVT算法具有更好的实现性能。而相比于IHT算法，当矩阵秩信息未知时，sEIRLS-0算法的性能具有明显的优势。未来的工作，结合非凸优问题，我们主要研究EIRLS-0和sEIRLS-0算法的实现效果和收敛率，并将其尽快应用于信息安全的数据处理研究领域。

[1] ARORA S, DASKALAKIS C, STEURER D. Message-passing algorithms and improvedlpdecoding[C]∥ Proc 41st annual ACM symposium on Theory of Computing, 2009:3-12.

[2] 周燕，张德丰，马子龙. 基于压缩感知的图像哈希水印算法研究[J].中山大学学报：自然科学版，2010，49(6)：58-63.

[3] CANDES E J，RECHT B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2009, 9(6):717-772.

[4] CANDES E J，BECKER S. Software for singular value thresholding algorithm for matrix completion[EB/OL]. Available at http://svt.caltech.edu/code.html. 2010.

[5] 杨海蓉,张成,丁大为,等.压缩感知理论与重构算法[J].电子学报,2011,39(1):142-147.

[6] CANDES E J, WAKIN M B, BOYD S. Enhancing sparsity by reweightedl1 minimization [J]. Journal of Fourier Analysis and Applications, 2008, 14(5):877-905.

[7] DAUBECHIES I, DEVORE R, FOMASIER M, et al. Iteratively re-weighted least squares minimization for sparse recovery[EB/OL]. http://arXiv.org/abs/0807.0575. 2008.

[8] MOHAN K ，FAZEL M. Reweighted nuclear norm minimization with application to system identification[C]∥ Proc. American Control Conference(ACC), 2010:2953-2959.

[9] CHARTRAND R, STANEVA V. Restricted isometry properties and nonconvex compressive sensing[J]. Inverse Problems, 2008, 24(035020):1-14.

[10] CHARTRAND R，YIN W. Iteratively reweighted algorithms for compressive sensing[C]∥ 33rd International Conference on Acoustics, Speech, and Signal Processing (ICASSP), 2008:3869-3872.

[11] KARTHIK M, MARYAM F. Iterative reweighted least squares for matrix rank minimization[C]∥Forty-Eighth Annual Allerton Conference, USA, 2010:653-661.

[12] GOLDFARD D, MA S. Convergence of fixed point continuation algorithms for matrix rank minimization[R]. Technical Report, Available at http://www.columbia.edu/sm2756/FPCAconvergence.pdf.2009.

[13] GROSS D, LIU Y K, FLAMMIA S T, et al. Quantum state tomography via compressed sensing[EB/OL]. Preprint available at http://arxiv.org/PS cache/arxiv/pdf/0909/ 0909.3304v2.pdf. 2010.

[14] 魏木生. 广义最小二乘问题的理论和计算[M].北京：科学出版社，2006：161-165.

[15] MEKA R, JAIN P, DHILLON I S. Guaranteed rank minimization via singular value projection[EB/OL]. Available at http://arxiv.org/ abs/0909. 2009:54-57.

[16] LEE K, BRESLER Y. ADMIRA: Atomic decomposition for minimum rank approximation[EB/OL]. Available at http://arxiv.org/abs/0905.0044. 2009.

[17] LU Z, PONG T K. Interior point methods for computing optimal design[EB/OL]. Available at http://arxiv.org/PS cache/arxiv/pdf/1009/ 1009.1909v1.pdf. 2010.

[18] 练秋生，周婷. 结合字典稀疏表示和非局部相似性的自适应压缩成像算法[J].电子学报，2012，40(7)：1416-1422.