Gorenstein合冲模的扩张封闭性
杨星星
(宿州学院 数学与统计学院,安徽 宿州 234000)
本文中,设R是左—右Noether 环,modR(modRop)表示由有限生成左R模(或右R模)组成的模范畴.众所周知,合冲模类具有很好的性质,对于任意正整数n,合冲模类都是函子有限的;另外,Auslander等[1]给出了诺特环上的合冲模与挠自由模的关系,并探讨两模类的扩张封闭性;Huang[2]研究了相对合冲模类的扩张封闭性;文[3]引入Gorenstein合冲模(以下简称G-合冲模)的概念,给出了G-合冲模类与挠自由模类的关系.本文探讨G-合冲模类的扩张封闭性(即:如果modR中正合列0 →A→B→C→0,若A,C是G-合冲模,则B是G-合冲模).
先来回顾一些后面要用到的基本知识.
我们把HomR(M,R)表示为M∗.对于一个左(或右)R模M,设:σM:M→M∗∗为M的典范同态,如果σM是单态射,模M为无挠的;如果σM是同构,模M为自反的.对于正整数k,模M∈modR为k-挠自由模,如果Exti R(TrM,R)=0,(1<i≤k),其中 TrM是模M的转置[2].易知:1- 挠自由模是无挠模,2- 挠自由模是自反模.本文用Tn(modR)表示由全体n-挠自由模组成的全子范畴.
定义1模M∈modR(或M∈modRop)被称为Gorenstein 投射的(简称G- 投射),如果满足(1)M是自反的.
定义2[4]对任意正整数n,模A∈modR,叫做左R模M的n-Gorenstein 合冲模,如果modR存在正合列 0 →A→Gn-1→ …G1→G0→M→0,其中所有的Gi都是G- 投射的.本文用G-Ωn(modR)表示全体n-Gorenstein合冲模组成的全子范畴,对偶地表示为G-Ωn(modRop).
定义3设M∈modR,i为任意非负整数,如果对任意 0≤j<i,有ExtRj(M,R)=0,则称模M的级数不小于i,记为GradeM≥i;如果对M的任意子模N都有GradeN≥i,则称模M的强级数不小于i,记为s.GradeM≥i.
显然,若s.GradeM≥i,则GradeM≥i,反之不成立.
引理4[5]下列陈述等价:
(1)对任意M∈modR,有GradeExtiR+1(M,R)≥i,其中1≤i≤k-1;
(2)对任意的1≤i≤k,有G-Ωi(modR)=Ti(modR).
下面给出G-Ω1(modR)的扩张封闭的结论.
定理5对任意N∈G-Ω1(modR),以下陈述等价:
(1)s.GradeExt1R(N,R)≥1;
(2)对 modR中的正合列 0 →L→M→N→0,若L∈G-Ω1(modR),则M∈G-Ω1(modR).
证明(1)⇒(2),对正合列应用典范同态σX:X→X∗∗,则容易得到如下交换图:

已知L,N∈G-Ω1(modR),于是σL和σN都是单的,由交换图可知:若f∗∗:L∗∗→M∗∗是单的,则可得σM是单的.事实上,对正合列,函子扩张后有如下正合列:
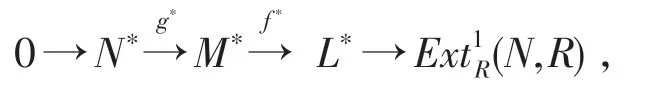
令K=co kerf∗,显然K为Ext1R(N,R)的子模,已知(1)中s.GradeExt1R(N,R)≥1,于是Hom(Ext1R(N,R),R)=0,即K∗=0,于是有,得f∗∗是单的,得证.
(2)⇒(1),设K为Ext1R(N,R)的任意子模,要证:s.gradeExt1R(N,R)≥1,只需证:K∗=0 即可.因为Ext1R(N,R)∈ modRop,则K为Ext1R(N,R)的有限生成子模,已知(2)中的正合列 0 →L→fM→gN→ 0 通过函子扩张以后有是正合的,因此,有下面的正合列交换图:
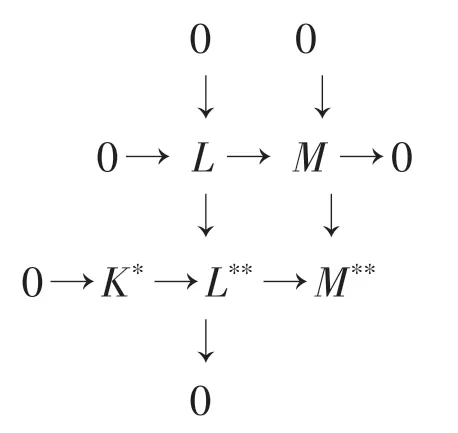
由交换图易知:K∗=0,于是有s.GradeExt1R(N,R)≥1.
引理6[2]以下陈述等价:
(1)对任意M∈modR,s.GradeExt1R(M,R)≥i,(1<i≤k);
(2)对任意的1<i≤k,有Ti(modR)是扩张封闭的.
下面给出本文的主要定理:
定理7对正整数k,有1<i≤k,以下陈述等价:
(2)G-Ωi(modR)是扩张封闭的;
(3)G-Ωi(modR)是扩张封闭的,且G-Ωi(modR)=Ti(modR).
证明(1)⇒(2):由(1)中,则由引理 4 可得:G-Ωi(modR)=Ti(modR),1<i≤k.设:N∈Ti(modR),于是N∈G-Ωi(modR),且在 modR中存在正合列:0 →N→Gi-1→ …G0→M→0,其中所有的Gi都是G-投射模,那么:M∈G-Ω-i(modR).所以由(1)可得于是由引理6可得:对任意的1<i≤k,有Ti(modR)是扩张封闭的,从而G-Ωi(modR)是扩张封闭的.
(2)⇒(3):K=1 显然,现设K≥2,利用数学归纳法,假设结论在 1<i≤k-1 时成立,即有:G-Ωi(modR)=Ti(modR)且G-Ωi(modR)是扩张封闭的,于是在modR中存在正合列:,其中所有的Gi都是G- 投射模,可得:Imfi∈G-Ωi(modR)=Ti(modR),1<i≤k-1,且有:,由G-Ωi(modR)在 1<i≤k-1 是扩张封闭的,可知在1<i≤k-1时,有Ti(modR)是扩张封闭的.由引理5有:对1<i≤k-1,有:

再由引理4可得:

(3)⇒(1):由于G-Ωi(modR)是扩张封闭的,且G-Ωi(modR)=Ti(modR),于是对1<i≤k,Ti(modR)是扩张封闭的,于是由引理5 可得:s.gradeExt1R(N,R)≥i,1<i≤k,N∈modR,还由正合列 0 →N→Gi-1→ …G0→M→0 可知:s.gradeExtiR+1(M,R)≥i且M∈G-Ω-i(modR),得证.
推论8对正整数k,有1<i≤k,以下陈述等价:
(1)s.gradeExtiR+1(M,R)≥i,M∈modR;
(2)G-Ωi(modR)是扩张封闭的;
(3)G-Ωi(modR)是扩张封闭的,且G-Ωi(modR)=Ti(modR).
[1]AUSLANDER M,REITEN I.Syzygy module for Northerian rings[J].Journal of Algebra,1996,183(1):163-185.
[2]HUANG Z Y.Extension closure of relative syzygy module[J].Science in China(Series A),2003,46(5):611-620.
[3]黄宠辉,谭良,蔡秋娥.Noether环上的Gorenstein合冲模[J].南华大学学报,2008,22(3):26-28.
[4]HUANG C H,HUANG Z Y.Gorenstein syzygy module[J].Journal of Algebra,2010,324:3408-3419.
[5]AUSLANDER M,BRIDGER M.Stalble module theory[M].Memoirs Amer Math Soc,Providence:AMS,1996.
[6]AUSLANDER M,REITEN I.K-Gorenstein algebras and syzygy module[J].Pure and Appl:Algebra,1994,92(1):1-27.

