The Jacobi Elliptic Function Method for Solving Zakharov Equation

WANG Qing

(Department of Basic Coures,Liaoning University of International Business and Economics,Dalian 116052,China)

The Jacobi Elliptic Function Method for Solving Zakharov Equation

WANG Qing

(Department of Basic Coures,Liaoning University of International Business and Economics,Dalian 116052,China)

The Zakharov equation to describe the laser plasma interaction process has very important sense,this paper gives the solitary wave solutions for Zakharov equation by using Jacobi elliptic function method.

Zakharov equation;Jacobi elliptic function method;solitary wave solution

§1.Introduction

Zakharov equation is a kind of important nonlinear evolution equation,it has a very rich physical background and connotation,the research from the son body movement or nonlinear waves of high frequency are involved in how to solve the Zakharov equation[1](numerical solution and exact solution),scholars pay close attention to the problem,gives some solving methods(such as[2-3]),this paper uses the Jacobi elliptic function method for solving Zakharov equation,obtained by this equation are obtained.

§2.Jacobi Elliptic Function Method

Jacobi elliptic function method for the main steps are as follows.

The f i rst step,for a given nonlinear evolution equation(Group)

As the traveling wave transformation

where λ is the wave speed.By ordinary dif f erential equation(Group)

The second step,a step of ordinary dif f erential equation(Group)(2.3)as the solution

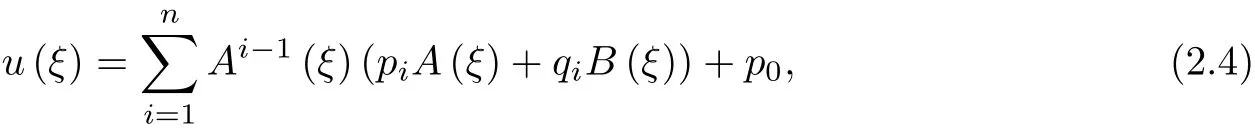
where n is a constant,it can get by balancing the highest derivative and non-linearity[2]and A(ξ),B(ξ)is a double projection Riccati equation with non zero solution,

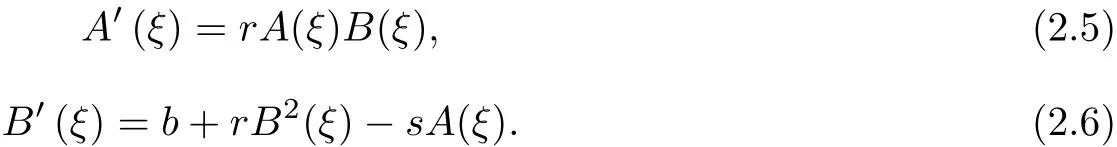
Based on the above relationship and[2-3],we give the equation(2.5)～(2.6)follows the formal solution.

When b2k20=b2l2+δ and br＜0,equations(2.5)and(2.6)have the following function solutions

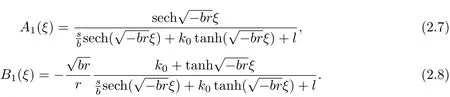
When b2k20=b2l2−δ and br＞0,equations(1.5)and(1.6)have the following trigonometric function solutions

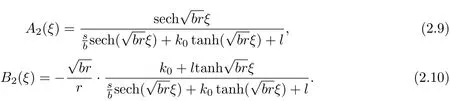
The third step,the formula(2.4)together with equation(2.5)～(2.6)substituted into equation(2.3)and the search for theAi(ξ)Bj(ξ)(i=0,1,···,n;j=0,1)coefficients,and then make the coefficient is 0,get on a variable p0,pi,qi,λ(i=1,···,n)overdetermined algebraic equations.

The fourth step,using Wu’s method(see[4])and Maple software for solving overdetermined equations,p0,pi,qi,λ(i=1,···,n),several solutions.

The f i fth step,the fourth step of each solution together with solutions group(2.7)～(2.9) and(2.10)into(2.4)and(2.2)type has the original equation(2.1)to the exact solution.

§3.Application of Jacobi Elliptic Function Method for Solving Zakharov Equation

The specif i c form of Zakharov equation as follows

Considering v is the electric f i eld intensity variations in the amplitude,we can set it into an envelope wave solutions and the ion number density deviation u for general travelling wave solutions.

Will(3.2)substituted into equation(3.1)to get

Will(3.3)the f i rst equation direct integral,integral constant is zero,so

Thus,for a real-valued function φ on c2g−c2sand u established requirements have the same sign.cg＜cs(subsonic),u from a negative number,cg＞cs(supersonic),u plus.

Will(3.4)type of substitution(3.3)of the second equation

Will(3.2)into(3.5),so

Let

Then(3.6)type of

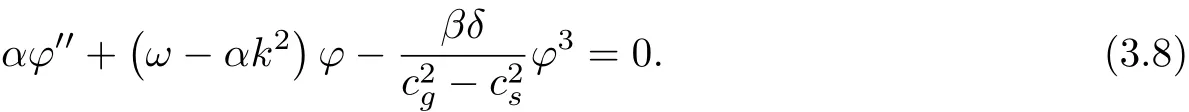
Will(3.7)type generation(3.8)type,there are

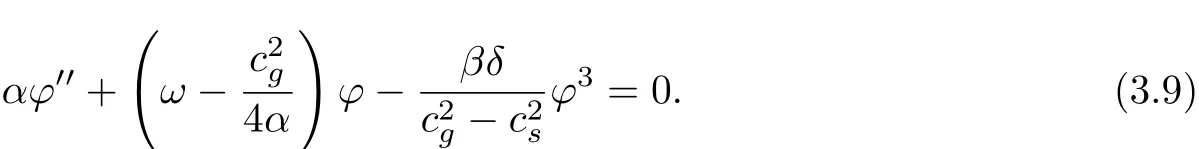
That is

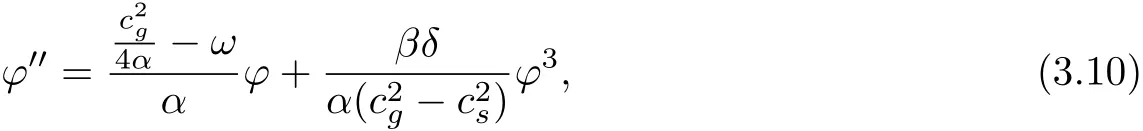
let

By[2],

Constraint condition

ψ(ξ)satisf i es the f i rst kind of elliptic equation

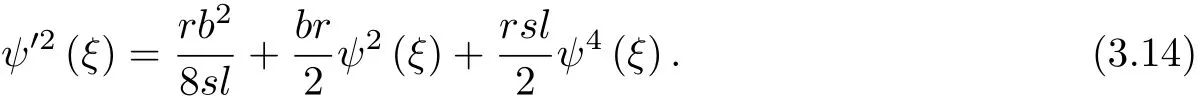
When the A(ξ),B(ξ)constraints

党的十九大提出了“实施乡村振兴战略”，推进乡村振兴，实现农业现代化，必须加快农业机械化步伐。站在新的历史起点，农业机械化引领农业生产方式变革的态势更加趋显，河南农机化发展又迎来了重大历史机遇。

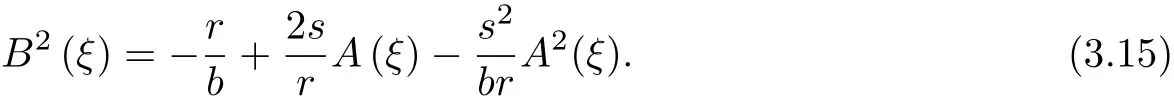
Equations(3.5)and(3.6)have the following elliptic function solutions

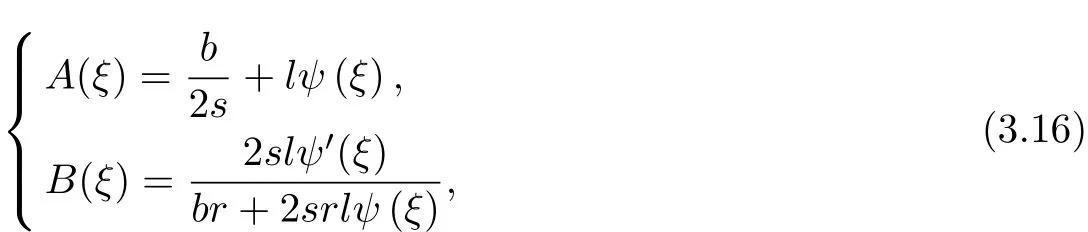
ψ(ξ)satisf i es the elliptic equation

Will(3.11)type of substitution(3.19)type and the use of(3.5),(3.6)and(3.12),the A(ξ) and B(ξ)of the power coefficient is zero,so

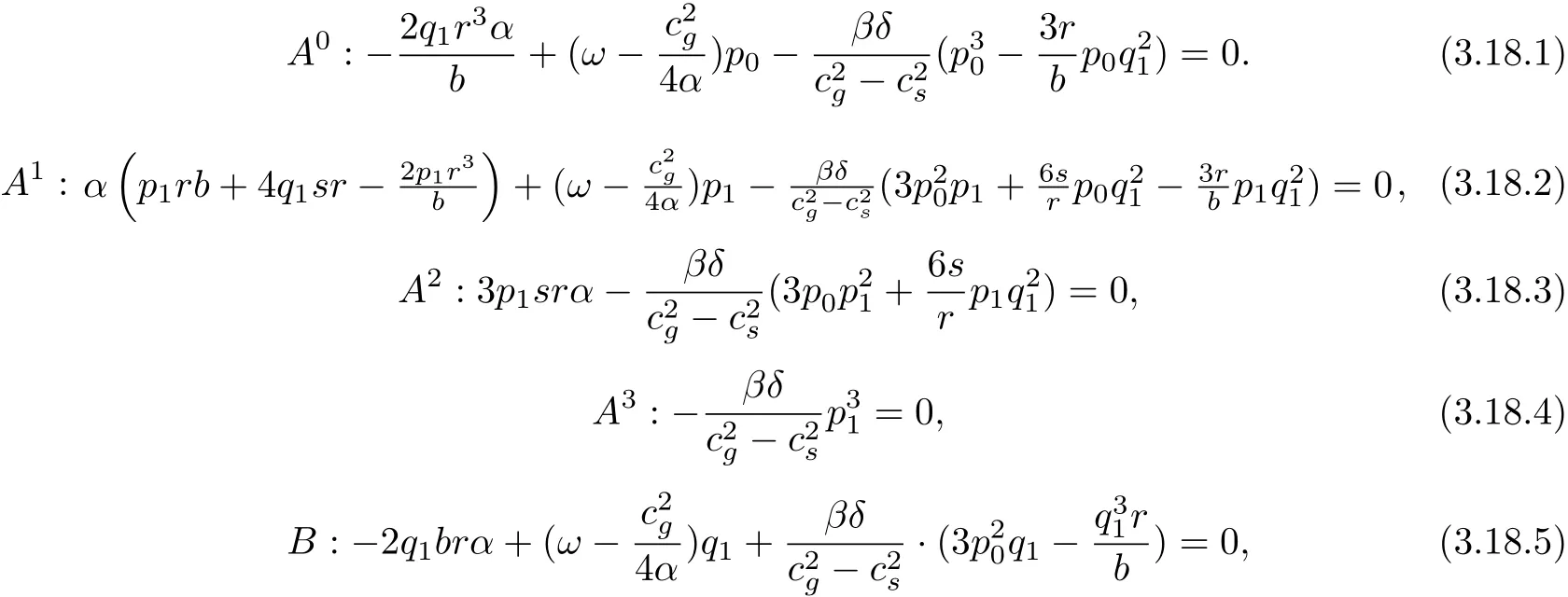
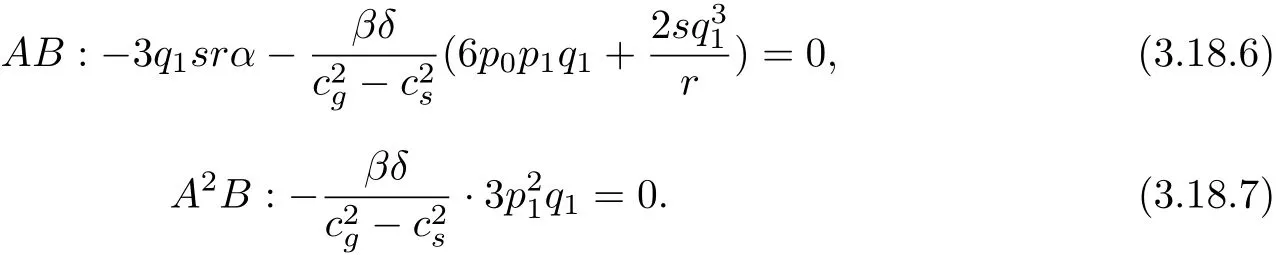
With Maple software solutions of the above equations,it can be

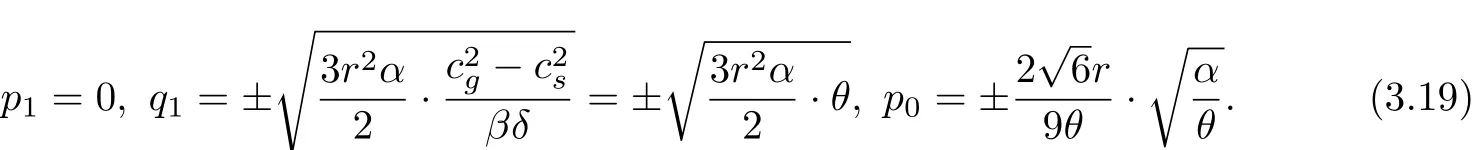
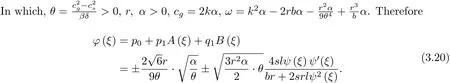
Will(3.20)type of substitution(3.12)and(3.14)type,we get Zakharov equation of a solitary wave solution

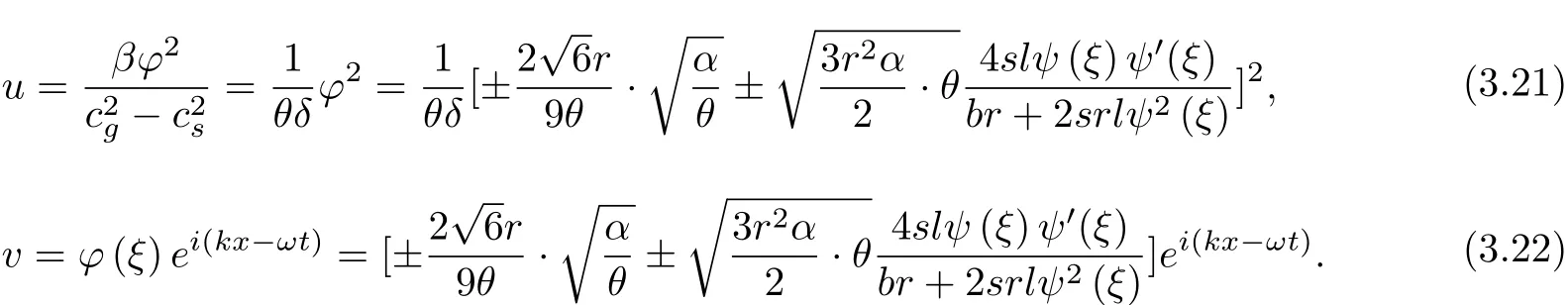
On the dif f erent values of r,b,s,l,ψ(ξ)correspond to dif f erent elliptic function.Will (3.11)type of substitution(3.9)type and use(3.5)～(3.6),(3.15),the A(ξ)and B(ξ)of the power coefficient is zero,so

With Maple software solutions of the above equations,it can be

In which

So

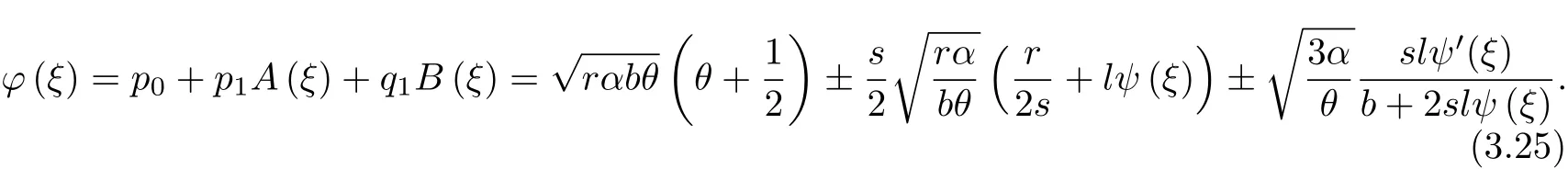
Will(3.25)type of substitution(3.2)and(3.4)type,we get Zakharov equation and a solitary wave solution

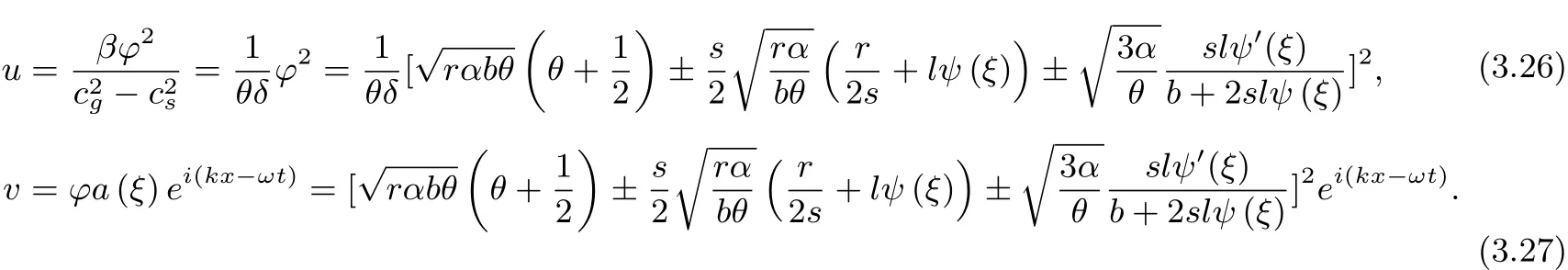
On the dif f erent values of r,b,s,l,ψ(ξ)correspond to dif f erent elliptic function.

§4.Summary

We use the Jacobi elliptic function method to solving Zakharov equation into the equation and obtained Zakharov equation new solitary wave solutions of Zakharov equation and gives the solutions to elliptic equations.Other suitable methods still need further discussion.

[1]LIU Shi-shi,LIU Shi-da.Nonlinear Equations in Physics[M].Beijing:Peking University Press,2000:157-200.

[2]LI De-sheng,ZHANG Hong-qing.Elliptic function solutions for nonlinear evolution equation have a simple and its applications[J].Acta Physical Sin,2006,55(4):1565-1570.

[3]ZHANG Shan-qing,LI Zhi-bin.New applications of Jacobi elliptic function expansion method[J].Acta Physical Sin,2003,52(5):1066-1069.

[4]YONG Xue-lin,ZHANG Hong-qing.Extended projective Riccati equations method and its application[J]. Acta Physical Sin,2005,54(6):2514-2519.

[5]WU W T.Polynomial Equation-solving and Its Application,Algorithms and Computation[M].Berlin: Springer-Verlage,1994:55-98.

tion:05A30

1002–0462(2014)04–0627–06

date:2013-11-11

Supported by the GHZD(13010)

Biography:WANG Qing(1974-),male,native of Liaoning,Dalian,an associate professor of Liaoning University of International Business and Economics,M.S.D.,engages in the numerical approximation.

CLC number:O155Document code:A