带无穷时滞两种群Lotka-Volterra离散模型的持久性
卞继承,范志强,徐加波,樊小琳
(新疆工程学院基础教学部,新疆 乌鲁木齐 830091)
带无穷时滞两种群Lotka-Volterra离散模型的持久性
卞继承,范志强,徐加波,樊小琳
(新疆工程学院基础教学部,新疆 乌鲁木齐 830091)
研究了一类无穷时滞两种群竞争Lotka-Volterra离散模型.通过构造李雅普诺夫函数,利用不等式的放缩技巧,给出了系统持久的充分条件.从而可知无穷时滞对种群的持久性没有影响.
持久性;种群离散模型;Lotka-Volterra系统;无穷时滞
1 引言
从20世纪80年代至今,国内外有许多研究工作[17]及其引用的参考文献,讨论了种群的持续生存及周期解的存在问题,并得到很多很好的结果.Lotka-Volterra模型就是生物种群动力学研究的一种非常重要的模型.
时滞在自然界中是经常发生的现象,研究时滞对系统的稳定性的影响是生物数学研究的一个重要课题.文献[8-10]就研究了具有时滞的离散模型.
本文中,主要对一类具有无穷时滞两种群的Lotka-Volterra离散模型进行了研究.
提出下列带无穷时滞非自治两种群Lotka-Volterra竞争系统:
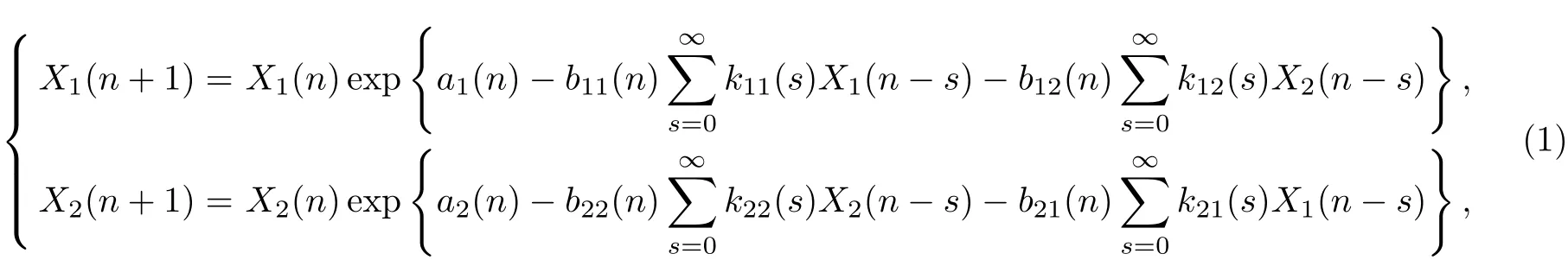
这里Xi(n)(i=1,2)表示时刻n时的种群密度.kij(i,j=1,2)是时滞核.
本文,将建立系统(1)持久的充分性条件,而且从结果中很容易看到无穷时滞对系统的持久性没有产生影响.本文的结果是对前人工作的一个推广.
2 基本假设和引理

本节,就系统(1),给出如下假设:
(H1)ai(n),bij(n)(i,j=1,2)是定义在上的非负有界序列,使得

(H2)kij(s)(i,j=1,2)对每一个s=0,1,2,···都是非负实数,而且满足

(H3)下面的不等式成立:
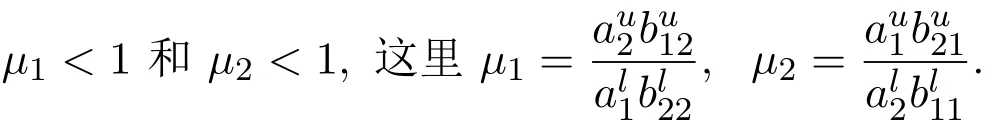
考虑到系统(1)的生物背景,本节只考虑系统(1)满足下列初始条件的解:

这里ϕ(θ)定义在θ=0,−1,−2,···上,而且满足ϕ(0)>0.
不难证明,系统(1)满足初始条件(2)的解都是正值,即,对n≥0,Xi(n)>0(i=1,2).
考虑下列非自治差分不等式:

这里α(n)和β(n)是定义在Z+上满足αl>0,βl>0的非负有界实数序列.
引理 2.1如果N(n)是不等式(3)满足N(0)>0的解,那么有
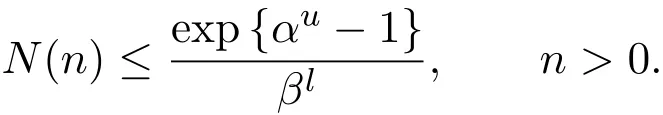
此引理证明比较简单,不再赘述.
引理 2.2如果 x(n)定义在 Z上的非负有界实数序列,H(n)是定义在上满足的非负有界实数列,那么

3 系统的持久性
接下来将建立系统(1)持久的充分条件.首先先给出系统最终有界的结果.
定理 3.1如果假设(H1)和假设(H2)成立,那么存在正常数Mi使得对系统(1)的满足初始条件(2)的任意正解(X1(n),X2(n))Xi(n)≤Mi,n>0,i=1,2.
证明对每一个i=1,2,因为存在一个整数 si0使得 0 所以 从而,对每一个i=1,2 因此,由引理2.1可知存在正常数Mi使得 定理 3.2如果假设(H1)-(H3)成立,那么存在正常数mi>0使得对系统(1)的任意正解(X1(n),X2(n)),有liminfn→∞Xi(n)≥mi,i=1,2. 证明设(X1(n),X2(n))是系统(1)的任意正解.由假设(H1),对系统(1)引入以下变换: 由变换(5)式和(6)式,利用引理2.2和定理3.1,可知对任意的n>0, 这里, 由(7)式和假设(H2),可知对n>1,有 由假设(H3),可以选取充分小的常数0<ε<1/2,使得 现在,定义一个区域Ω如下.首先定义两条曲线γ和Γ, 接下来将证明z(n)=(x1(n),(n))最终会进入区域Ω并最终保持在其中.为此,首先来证明z1(n)=(x1(n),x2(n))最终位于曲线γ的右侧.为此,先给出两个重要的命题. 命题 3.1存在正整数N0>0使得x1(N0)≥ω. 事实上,如果对n>0,x1(n)<ω.那么由(12)式,可得 这表明当n→∞时V(n)→∞.所以,由(10)式进一步可得 同时,由引理2.2,存在正常数T0,使得 在前面的假设之下,由引理2.2,存在正整数T1≥T0,使得 因此,由(1),(5),(14)-(16)式,对n≥T1,有 因此,当n→∞时x1(n)→∞.这导出一个矛盾.命题3.1证明结束. 命题 3.2对任意p>0,如果x1(p)≥ω,那么z(p+1)位于曲线γ的右侧,同时 因此,由(7)式,有 事实上,如果x1(p)≥ω,那么由系统(1)第一个方程,可得 这和z(p+1)位于曲线γ的右侧矛盾.命题3.2证明结束. 现在,用上面的命题证明z(n)最终位于曲线γ的右侧.由命题3.1,存在正整数N0>0,使得x1(N0)≥ω.接下来证明对n≥N0,z(n)位于曲线γ的右侧.否则,由命题3.2,存在整数≥N0+1,使得对N0≤n≤,z(n)位于曲线γ的右侧并且z+1)位于曲线γ的左侧,即, 因此,由命题3.2可得x1()<ω.因为x1(N0)≥ω,存在整数满足N0<≤,使得 进而,注意到x1(−1)≥ω,那么由命题3.2,可得 由(12)式,可知 结合(10)式,有 这表明 这和 (17)式矛盾.根据上面的论证,可以得到:对 n≥N0,z1(n)=(x1(n),x2(n))位于曲线 γ的右侧.类似的可以证明 z2(n)=((n),(n))最终会位于曲线 Γ的上方.因此, z(n)=(x1(n)(n))最终会进入并保持在区域Ω内.这表明 最后,由变换(5)式和(6)式,最终可得存在常数 mi使得liminfn→∞Xi(n)≥mi,i=1,2,定理3.2证明结束. 本文就带无穷时滞两种群竞争离散模型的持久性进行了研究.但是带有无穷时滞离散种群系统的全局吸引性仍然是一个开问题,在处理无穷时滞的时候遇到很大的困难,因此种群全局吸引性将在后续工作中加以讨论. [1]Teng Zhidong.Uniform persistence of the periodic predator-prey Lotka-Volterra systems[J].Appl.Anal., 1999,72:339-352. [2]Cui Jingan,Sun Yonghong.Permanence of predator-prey system with inf i nite delay[J].Electronic Journal of Dif f erential Equations,2004,81:1-12. [3]Lu Zhengyi,Wang Wendi.Permanence and global attractivity for Lotka-Volterra dif f erence systems[J].J. Math.Biol.,1999,39(3):269-282. [4]樊小琳,秦丽华,刘艳.捕食者非密度制约的捕食食饵模型的持久性[J].纯粹数学与应用数学,2011,27(4):459-471. [5]王晖.一类基于比率的且具有收获率和时滞的捕食系统的周期解[J].纯粹数学与应用数学,2013,29(5):520-528. [6]田德生.三阶常系数拟线性泛函微分方程的周期解[J].纯粹数学与应用数学,2013,29(3):233-240. [7]Li Yongkun,Zhu Lifei.Existence of positive periodic solutions for dif f erence equations with feedback control [J].Applied Mathematics Letters,2005,18:61-67. [8]Chen Fengde.Permanence of a single species discrete model with feedback control and delay[J].Applied Mathematics Letters,2007,20:729-733. [9]Saito Y,Ma Wanbiao,Hara T.A necessary and sufficient condition for permanence of a Lotka-Volterra discrete system with delays[J].J.Math.Anal.Appl.,2001,256(1):162-174. [10]Saito Y,Hara T,Ma Wanbiao.Harmless delays for permanence and impersistence of a Lotka-Volterra discrete predator-prey system[J].Nonlinear Anal.,2002,50:703-715. Permanence of two species Lotka-Volterra discrete system Bian Jicheng,Fan Zhiqiang,Xu Jiabo,Fan Xiaolin In this paper,a Lotka-volterra competitive discrete system with inf i nity delay is investigated.By constructing Lypunov functions,an sufficient conditions for the permanence of the system has been established. From the result,we f i nd that the inf i nity delay does not ef f ect the permanence of the system. permanence,species discrete system,Lotka-Volterra system,inf i nite delay O178 A 1008-5513(2014)02-0166-07 10.3969/j.issn.1008-5513.2014.02.007 2014-03-10. 国家自然科学基金(11301451);新疆自治区高校科研计划(XJUEDU2013S44). 卞继承(1976-),硕士,讲师,研究方向:小波分析及应用. 樊小琳(1979-),博士生,副教授,研究方向:微分方程的应用. 2010 MSC:39A30,92D25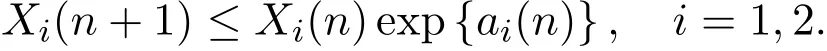


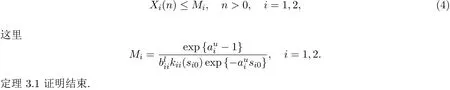
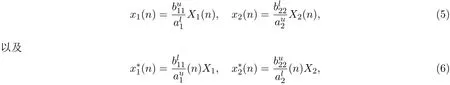






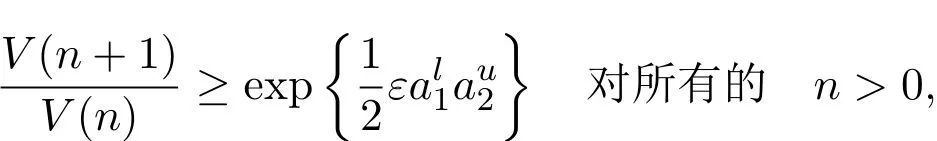
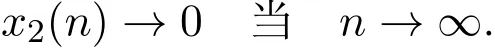



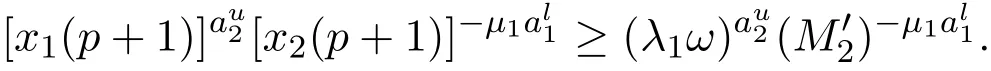





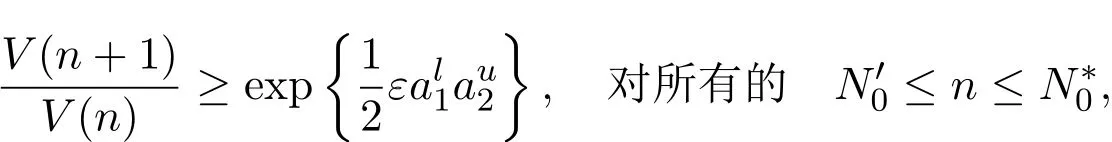
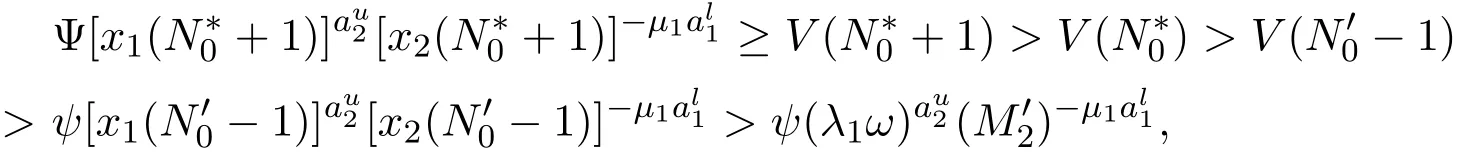
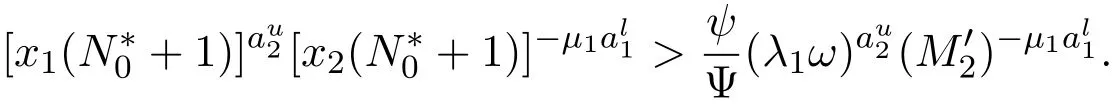

3 讨论
with inf i nite delay
(Department of Fundamental Education,Xinjiang Institute of Engineering,Urumqi830091,China)

