近Kaehler流形S3×S3上的殆切触拉格朗日子流形
杨标桂,朱晴晴
(福建师范大学数学与计算机科学学院,福建福州350108)
近Kaehler流形S3×S3上的殆切触拉格朗日子流形
杨标桂,朱晴晴
(福建师范大学数学与计算机科学学院,福建福州350108)
对于近Kaehler流形S3×S3上的一个拉格朗日子流形M,给出由M上的一个单位向量场典范引出的殆切触度量结构是α-Sasakian的充要条件.当这个殆切触度量结构为切触度量结构时,给出了这个切触度量结构是Sasakian结构的充分必要条件.关键词:近Kaehler流形;拉格朗日子流形;(殆)切触度量结构;Sasakian结构
1 引言
1970年,文献[1]系统地研究了近Kaehler流形,这些近Kaehler流形是带有复结构J的殆Hermitian流形,这里张量场¯∇J是反对称的.近Kaehler 6维球面S6的子流形已被许多人研究过(参见文献[2-4]).近年来,文献[5]中阐述了齐性6维近Kaehler流形只包括近Kaehler流形S3×S3,射影空间CP3和旗流形SU(3)/U(1)×U(1),这些空间都是紧致的3维对称空间.众所周知,一般情况下近Kaehler流形的子流形分为殆复子流形和全实子流形,而拉格朗日子流形为全实子流形的一种.文献[6]系统地介绍了近Kaehler流形S3×S3的殆复曲面,本文将初步研究S3×S3的殆切触拉格朗日子流形.旨在找出由S3×S3的拉格朗日子流形上的一个单位向量场典范引出的殆切触度量结构是α-Sasakian的充要条件,并且讨论这个殆切触子流形为切触子流形时的情形.
2 预备知识

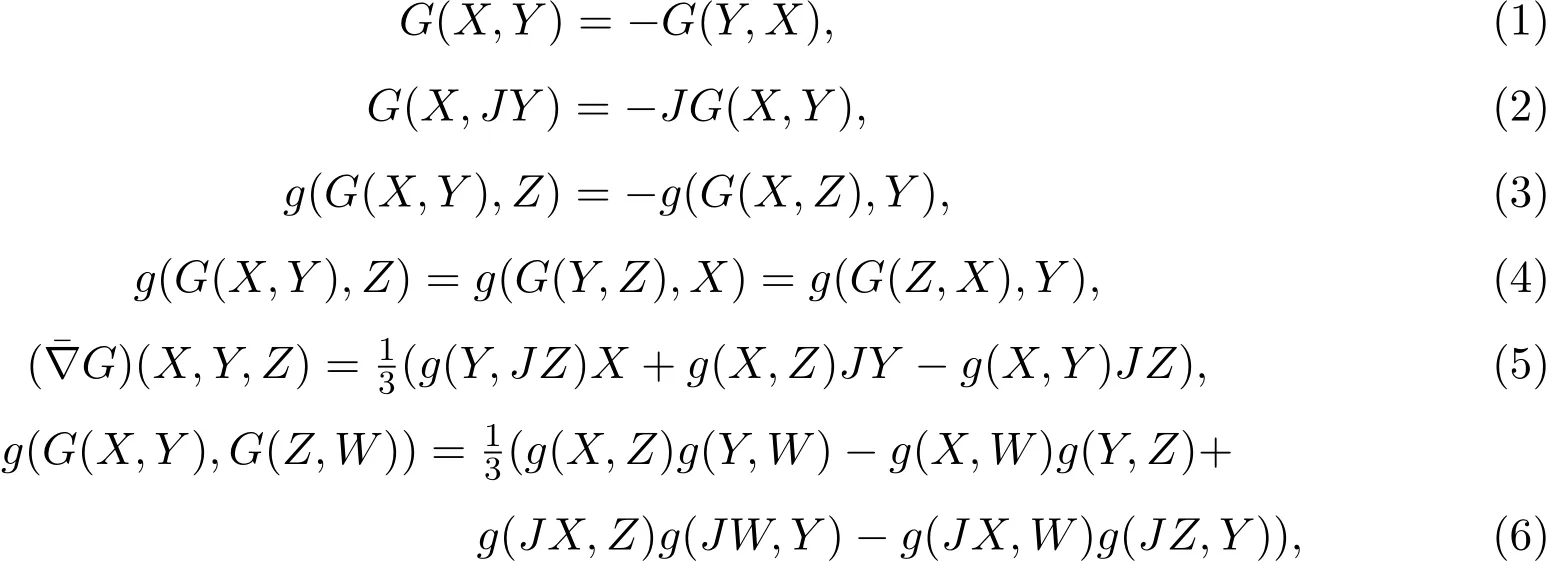

其中X,Y∈TM,ξ∈T⊥M.第二基本形式σ和形状算子Aξ之间有如下关系式:

回顾殆切触度量流形的相关知识[7-8].一个(2n+1)维光滑流形M称为殆切触度量流形,若∀X,Y∈TM,M上存在一个整体1形式η,一个单位向量场ξ,一个(1,1)-型张量场φ和黎曼度量g满足下列方程:

显然

若满足dη(X,Y)=g(X,φY),则M上的殆切触度量结构(M,η,,g)称为切触度量结构.


当h=0时,称为K-切触度量流形.殆切触度量流形若满足(∇Xφ)Y=α(g(X,Y)ξ−η(Y)X),则称为α-Sasakian流形,其中∇是关于g的黎曼联络.特别地,若α=1,这个切触度量流形就是Sasakian流形.切触度量流形是K-切触度量流形当且仅当Ric(X,ξ)=2nη(X).在维数为3的情况下,K-切触条件等价于Sasakian条件.
3 主要结果
首先,给出如下引理.
引理3.1设M为S3×S3的一个拉格朗日子流形,∀X,Y∈TM,有G(X,Y)∈T⊥M.
证明由(7)式和(8)式可得:

其中X,Y,Z∈TM.(1)式和(3)式表明上式右边互相相等.因此有g(G(X,Y),Z)=0,这表明G(X,Y)正交于M.
其次,有如下结果.
引理3.2设M为S3×S3的一个拉格朗日子流形,∀X,Y,Z∈TM,有

证明由(1)式和(2)式知,∀X,Y,Z∈TM,有
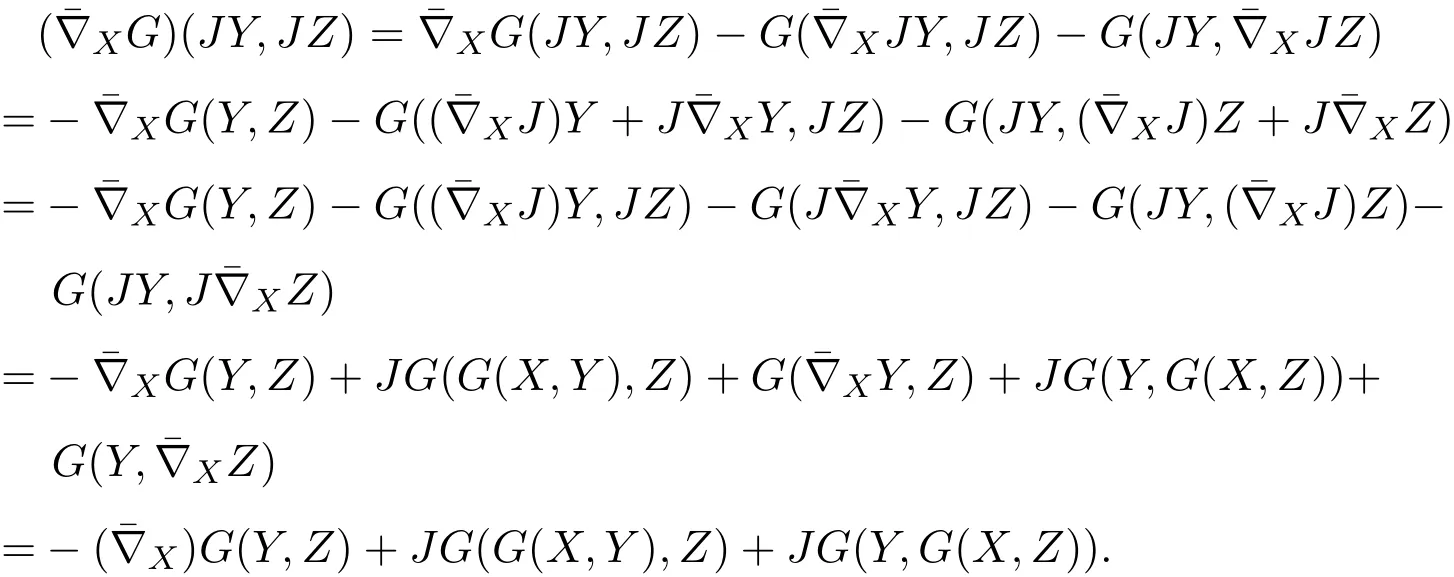
结合(5)式,得到
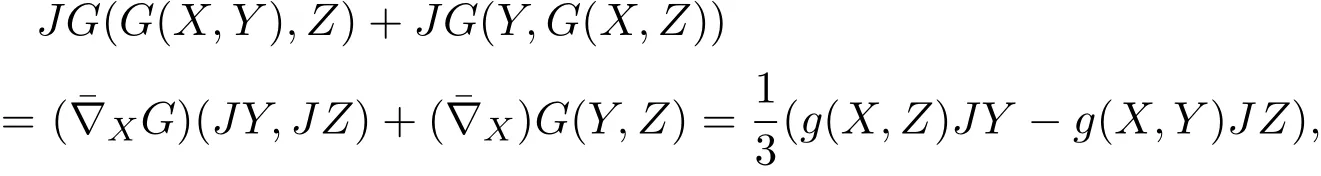
即
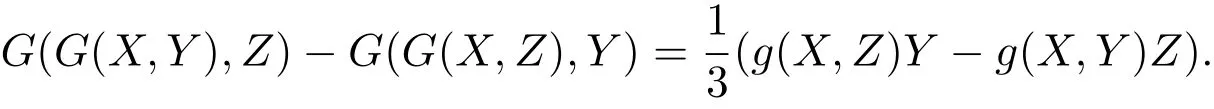
因此

或者等价于
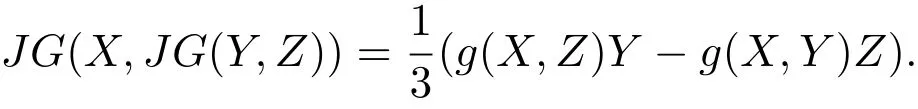
再次,令ξ是M上的一个单位向量场,遵从M上的度量g,定义一个1形式η满足η(X)=g(X,.由(2)式可知,∀X∈TM,向量场G(X,J)=−JG(X,),由引理3.1可知,G(X,J)∈TM.因此给出如下引理:
引理3.3的拉格朗日子流形(M,g)上的一个单位向量场ξ,引出一个典范殆切触度量结构(φ,g,),其中结构张量φ定义为
证明由定义知φ(ξ)=0,从(1)式和(2)式可以得到,对∀X,Y∈TM,有

另外

结合引理3.2,可得
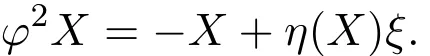
又由(6)式得到,
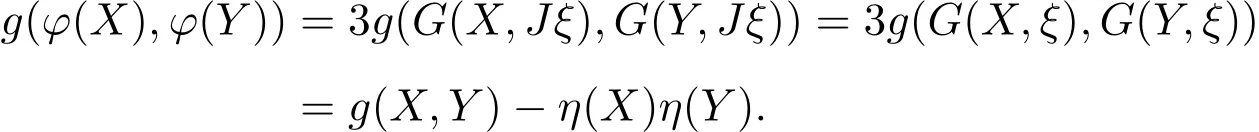
给出如下定义:
定义3.1(φ,,η,g)称为M上的典范殆切触度量结构,其中单位向量场由上述引理定义.
定理3.1令M为的一个拉格朗日子流形,带有近Kaehler结构(g,J),是M上的一个单位向量场,带有典范引出的M上的殆切触度量结构(φ,g,),则这个结构是的当且仅当F=0.
证明由引理3.3,计算出φ的共变导数

将(5)式和(8)式代入上式,得

通过比较上述等式左右两端的切向分量,有

可知,若F=0,则

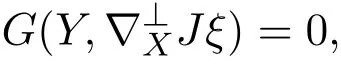
即
用ξ代替Y,可得φFX=0.等式两边用φ作用便得F=0.
此外,还可以得到如下结果:
定理3.2令M为的一个拉格朗日子流形,带有近Kaehler结构(g,J),是M上的一个单位向量场.假设由典范引出的M 上的殆切触度量结构(φ,g,)是切触度量结构,
证明由(7)式-(8)式和引理3.3可得,


成立.因此就有

又由文献[8]知:div(hφ)(X)=Ric(ξ,X)−2η(X).得

[1] Gray A.Nearly Kaehler manifolds[J].J.Di ff.Geom.,1970,4:283-309.
[2] Deshmukh S,EI Hadi K.A Sasakian structure on a 3-dimensional totally real submanifold of the nearly Kaehler 6-sphere[J].Panamer Math.J.,1992,3:43-52.
[3] Dillen F,Opozda B,Verstraelen L,et al.On totally real 3-dimensional submanifold of the nearly Kaehler 6-sphere[J].Proc.Am.Math.Soc.,1987,99:741-749.
[4] Ejiri N.Totally real submanifolds in a 6-sphere[J].Proc.Am.Math.Soc.,1981,83:759-763.
[5] Butruille J.B.Homogeneous nearly Kaehler manifolds.Handbook of Pseudo-Riemannian Geometry and Supersymmetry[M].IRMA Lect.Math.Theor.Phys.,16,Eur.Math.Soc.,Zu¨rich,2010.
[6] Bolton J,Dillen F,Dioos B,et al.Almost complex surfaces in the nearly kaehler S3×S3[J].ArXiv:1208. 0737.Preprint,2013.
[7] Blair D.E.Riemannian Geometry of Contact and Symplectic Manifolds[M].Sec.edi.Progress in Mathematics,203.,Boston,MA:Birkh¨auser Boston,Inc,2010.
[8] Blair D.E,Sharma R.Generalization of Myers′theorem on a contact manifold[J].Illinois Journal of Mathematics,1990,34:837-844.
Almost contact Lagrangian submanifolds of nearly Kaehler
Yang Biaogui,Zhu Qingqing
(School of Mathematics and Computer Science,Fujian Normal University,Fuzhou350108,China)
For a Lagrangian submanifold of the nearly Kaehler S3×S3,we provide a necessary and sufficient condition for a canonically induced almost contact metric structure by a unit vector fi eld,to be α-Sasakian. Furthermore,assuming the almost contact metric structure is contact metric structure,we give a necessary and sufficient condition in which the contact metric structure is Sasakian.
nearly Kaehler manifold,Lagrangian submanifold,(almost)contact metric structure, Sasakian structure
O186
A
1008-5513(2014)05-0454-06
10.3969/j.issn.1008-5513.2014.05.003
2014-07-26.
国家自然科学基金(11171139,11326045,11401099);福建省自然科学基金(2011J05001);福建省教育厅A类项目(JA11052).
杨标桂(1976-),博士,副教授,研究方向:微分几何.
2010 MSC:53D15

