锥 b-Banach空间的不动点定理

鲍宝国，卢冬晖

(湖北师范学院 数学与统计学院， 湖北 黄石 435002)

锥 b-Banach空间的不动点定理

鲍宝国，卢冬晖

(湖北师范学院 数学与统计学院， 湖北 黄石 435002)

通过新定义锥b-Banach 空间的概念，推广了锥Banach 空间的概念，并推广了Karapinar的两个不动点定理。

锥Banach 空间;锥 b-Banach空间;不动点

在2007年，黄龙光和张宪[1]通过用借助锥而定义的半序来代替实数之间的半序定义出锥度量空间的概念，之后，很多建立在锥度量空间的不动点定理被发表出来[2，3]。Hussain N和Shah M H[4]在2011年又在锥度量空间的基础之上，提出了锥b-度量空间，它讨论的范围比锥度量空间更大。最近，一个与锥度量空间紧密相关的锥Banach空间[5]被定义出来，Karapinar[6]把一些著名的度量空间的不动点定理推广到这个空间。

在本文中，作者通过新定义锥b-Banach 空间的概念，推广了锥 Banach空间的概念，而且推广了Karapinar[6]的两个不动点定理。

首先我们需要了解下面的定义。

定义1[1]设X是一个非空集合，d:X×X→E,满足下列条件：

1)d(x,y)≥θ(∀x,y∈X),d(x,y)=θ⟺x=y;

2)d(x,y)=d(y,x);

3)d(x,y)≤d(x,z)+d(z,y)(∀x,y,z∈X)

称d为X上的一个锥距离或锥度量，同时称(X,d) 为锥度量空间或锥距离空间.

定义2[5]设X是一个向量空间，映射 ‖·‖c:X→E满足：

1)‖x‖c≥θ(∀x∈X),‖x‖c=θ⟺x=θ;

2)‖x+y‖c≤‖x‖c+‖y‖c(∀x,y∈X);

3)‖kx‖c=|k|‖x‖c(∀k∈,∀x∈X)

称 ‖·‖c为X上的一个锥范数，同时称 (X,‖·‖c)为锥赋范空间.

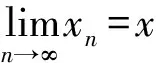
2) 设(X,‖·‖c) 为锥赋范空间，{xn} 为X中的序列，如果对于每个满足c≫θ的c∈E, 这里总存在一个自然数N, 使得对于所有的n,m>N, 都有‖xn-xm‖c≪c, 那么称{xn} 为X中的Cauchy列.

3) 若对X中的每个Cauchy列都收敛，称 (X,‖·‖c)为完备的锥赋范空间.完备的锥赋范空间被称为锥Banach空间。

定义4[4]设X是一个非空集合，d:X×X→E, 满足下列条件：

1)d(x,y)≥θ(∀x,y∈X),d(x,y)=θ⟺x=y;

2)d(x,y)=d(y,x);

3)d(x,y)≤sd(x,z)+sd(z,y)(∀x,y,z∈X);

称d为X上的一个锥b度量，同时称(X,d) 为锥b度量空间.

1 主要结果

定义5 设X是一个向量空间，映射‖·‖c:X→E满足：

1)‖x‖≥θ(∀x∈X),‖x‖c=θ⟺x=θ;

2)‖x+y‖c≤s‖x‖c+s‖y‖c(∀x,y∈X);

3)‖kx‖c=|k|s‖x‖c(∀k∈,∀x∈X)

称 ‖·‖c为X上的一个锥b范数，同时称(X,‖·‖c)为锥b赋范空间.

完备的锥b赋范空间被称为锥b-Banach 空间。任意的锥b赋范空间都是锥b度量空间，实际上，我们可以令d(x,y)=‖x-y‖c.

例1 设X=R2，P={(x,y):x≥0,y≥0}⊂R2,及 ‖(x,y)‖c=(|x|2,|y|2).那么(X,‖·‖c)是一个锥b-Banach 空间。

注释1 定义5推广了定义2，因为只要在定义5中令s=1，即可得到定义2，而且例1也足以支撑定义5中的锥b-Banach 空间是存在的。

定理1 设C是锥b-Banach 空间(X,‖·‖c)上的凸闭集，且定义‖x‖c=d(x,0) ，映射T:C→C满足：

d(x,Tx)+d(y,Ty)≤qd(x,y)

(1)

对任意x,y∈C,0≤q<3s，那么T存在至少一个不动点。

证明 令x0为C中任意一点，定义{xn} ：

(2)

我们可得到d(xn,Txn)=‖xn-Txn‖c=3sd(xn,xn+1)

(3)

结合(1)式，我们可得到：

3sd(xn-1,xn)+3sd(xn,xn+1)≤qd(xn-1,xn)

d(z,Tz)+3sd(xn,xn+1)≤qd(z,xn)

令n→∞时，我们可得到Tz=z。

注释2 定理1不仅在空间上推广了Karapinar[6]的定理2.5，而且推广了他的定理2.5中压缩条件的系数。

定理2 设C是锥b-Bbanach 空间(X,‖·‖c)上的凸闭集，且定义‖x‖c=d(x,0) ，映射T:C→C满足：

d(Tx,Ty)+d(x,Tx)+d(y,Ty)≤rd(x,y)

(4)

证明 构造定理1中的数列{xn} ，那么(2)，(3)式都满足，且

(5)

因为d(xn,Txn)-sd(xn,Txn)≤sd(Txn-1,Txn)

考虑到(3)，(5)式，我们得到

3sd(xn,xn+1)-s·2sd(xn-1,xn)≤sd(Txn-1,Txn)

易得 3sd(xn,xn+1)-s·3sd(xn-1,xn)≤sd(Txn-1,Txn)

(6)

令x=xn-1,y=xn代入(4)式中且考虑到(3)，(5)，(6)式，我们得到

我们令x=z,y=xn，代入(4)式，得

d(Tz,Txn)+d(z,Tz)+d(xn,Txn)≤rd(z,xn)

所以Tz=z.

注释3 定理2不仅在空间上推广了Karapinar[6]的定理2.6，而且推广了他的定理2.6中压缩条件的系数。

[1]Huang L G, Zhang X.Cone metric space and fixed point theorems of contractive mappings[J]. J Math Anal Appl,2007,332:1468～1476.

[2]Cho S H, Bae J S.Common fixed point theorems for mappings satisfying property (E. A) on cone metric space[J]. Mathematical and Computer Modeling,2011, 53:945～951.

[3]Cho Yeol Je, Saadati Reza, Wang Shenghua.Common fixed point theorems on generalized distance in ordered cone metric spaces[J].J Computers and Mathematics with Applications, 2011,61:1254～1260.

[4]Hussain N,Shah M H.KKM mapping in cone b-metric spaces[J].J Computers and Mathematics with Applications,2011,62:1677～1684.

[5]Abdeljawad T, Turkoglu D, Abuloha M.Some theorems and examples of cone metric spaces[J]. J Comput Anal Appl,2010,12(4): 739～753.

[6]Karapinar E.Fixed point theorems in cone Banach spaces[J]. Fixed Point Theory Appl,2009: 1～9.

Fixedpointtheoremsinconeb-Banachspaces

BAO Bao-guo,LU Dong-hui

(College of Mathematics and Statistics, Hubei Normal University,Huangshi 435002,China)

In this paper,we introduce a concept of cone b-Banach space,using this concept,we prove two fixed point theorems,which generalize the correspondly results obtained by karapinar.

cone Banach space;cone b-Banach space;fixed point

2013—12—29

鲍宝国(1988— )，男，陕西韩城人，硕士研究生，主要从事不动点理论的研究.

O177.91

A

1009-2714(2014)02- 0058- 03

10.3969/j.issn.1009-2714.2014.02.013