二维晃动模态的统一Ritz计算格式
李遇春,张 皓
(同济大学 水利工程系,上海 200092)
晃动是一种常见的发生在贮液结构中的物理现象。在土木、水利、化工、造船及航空航天工程中,常常遇到各种形状的贮液结构,如净水池、水塔、水库、渡槽、储油罐、液化气运输船以及燃料箱等,为保证贮液结构的可靠性,在结构设计时,需要首先了解容器内液体的晃动模态。
Dodge等[1-3]在他们的专著中对流体晃动的一般理论及工程应用进行了全面而系统的阐述。流体晃动模态分析方法有:变分法[4-5],积分方程法[6],保角映射法[7-8]、双坐标法[9]、其它解析方法[10]以及诸多的数值方法[11],文献[12-13]对三维晃动模态分析方法进行了分析总结。
在土木、水利工程领域,许多三维晃动问题常常可按二维晃动问题进行处理,例如:不同形状的TLD(调频液体阻尼器)、大型渡槽的内流体的横向晃动等都可以按二维晃动进行分析。二维矩形截面内液体晃动的模态问题已得到了充分的研究,然而对于非矩形截面内的二维晃动模态问题研究不够充分,所采用的计算方法不具一般性,仅用于解决特定的问题,例如:Hasheminejad等[8]采用保角映射的方法研究了半椭圆截面内液体晃动模态的求解方法,但其计算公式只能适合半椭圆容器,最近Li等[14]基于Ritz方法提出了一个针对不同截面内的二维晃动频率的简单近似解析方法,但计算精度有限,与其它解析与数值解的误差在5%的范围内,若希望得到更高精度的频率解时,这个方法不再适用,这个方法难以获得可靠的晃动振型。
本文亦基于Ritz方法,通过引入Green公式,借助矩形截面晃动模态的精确解,针对任意二维截面形状,采用统一的基函数,避免针对不同截面(由于边界条件的不同)需要引入不同基函数的复杂性,使得Ritz方法在理论上适用于任意截面的二维晃动模态分析,可同时得到可靠的晃动频率与振型,计算精度可以通过选取基函数的多寡进行调整,可完全满足工程计算要求。
1 二维自由晃动基本方程
如图1所示为任意的二维(对称)形状截面,建立直角坐标系OXZ,符号Ω,Sf和Sw分别表示静止液体区域,液体自由表面和湿边界。x轴与液体自由表面重合,z轴垂直向上并通过自由表面的中点。自由表面的宽度为2a,容器假定为刚体。

图1 任意形状截面Fig.1 An arbitrary-section
基于线性势理论,不考虑表面张力作用,假定流体为无粘,无旋且不可压缩的液体,假设液体自由表面的晃动幅度较小,那么其晃动问题可由下列的线性化方程来描述:

式中:(x,z,t)为速度势函数,hf(x,z,t)为自由表面上的波高函数,t为时间,g为重力加速度,n为湿边界的外法线,/n为湿边界外法线方向的导数。
为了求解方程组(1)-(4),可以假定方程具有以下形式的解:

式中是晃动(圆)频率,函数(x,z)和f(x,z)分别表示函数 Φ(x,z,t)和 hf(x,z,t)的幅值,将表达式(5),(6)代入方程组(1)-(4),同时合并方程(3)(4),可以得到如下的特征值问题:


式中:特征值λ与晃动(圆)频率ω之间的关系为:

根据图1的液体区域Ω,引入平面Green定理:

式中:S=Sw+Sf,P与Q为封闭区域Ω内连续可微的函数,若定义:

将式(12)代入方程(11),并利用方程(7)得到:

式中:s表示曲线坐标,在边界S上沿逆时针方向为正。τx=cos(τ,x)及 τz=cos(τ,z)为切向量 τ(见图 1)的方向余弦,切向量与外法向量的方向余弦有如下的关系:

式中:nx=cos(n,x)与 nz=cos(n,z)为外法向量 n(见图1)的方向余弦。将式(14)代入方程(13),将S上的积分分解为边界Sf与Sw上的和,利用方程(8)和(9),最后可以得到:

式(15)为晃动频率ω在二维情形下的Rayleigh商表达式。
2 Ritz求解方法
式(15)可以改写为:

利用Ritz方法求解方程(16),可将函数表达为一组完备基函数的线性组合:

其中:αT=(α1,…,αm)为待定系数向量
=(φ1,…,φm)为基函数向量
将表达式(17)代入式(16)可以得到:

如果记:

则式(18)可以写为:

方程(20)为广义特征值问题,矩阵A,B为实对称矩阵,若基函数向量 φT=(φ1,…,φm)已知,解此特征值问题,可求得m个特征值与特征向量为λj,αTj(j=1,2,…,m),根据方程(10)(17)可以得到流体系统的前m阶晃动频率与振型函数。
3 Ritz基函数的构造
3.1 矩形截面基函数及其模态解
如图2所示矩形截面的静止流体宽度为2a0,深度为H。

图2 矩形截面Fig.2 A rectangular section
引入无量纲变量 x=X/a0,z=Z/a0,无量纲液深h=H/a0,构造基函数 φj(x,z),可将其分离为两个独立函数 ξj(x)和 ηj(z)之积:

显然:函数ξj(x)表示自由液面的第j阶模态振型,基函数 φj(x,z)应满足方程(7)~(9),将 φj(x,z)代入方程(7)~(9),求解之,可以得到基函数 φj(x,z)及模态频率ω2j如下:

式中:
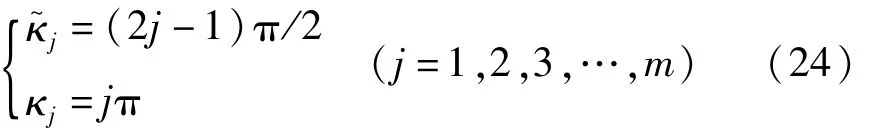
可以发现式(22),(23)满足 Laplace方程(7)及边界条件式(8),(9),为特征值问题的精确解析解。其第j阶自由表面的模态函数分别为(反对称模态)及 cosκjx(正对称模态)。
3.2 任意截面基函数及其模态解
如图3,记 Ω0为矩形计算区域,Sf0和Sw0分别为其自由表面和湿边界,其相对应的基函数记为φi,特征值为需要求解的任意计算域Ω位于矩形区域Ω0中,并且两者的自由表面Sf和Sf0相重合,为矩形区域Ω0与待求解域Ω之差,ΔSf为两者自由表面Sf0以及Sf之差。
对于任意截面Ω内的液体,若采用的Ritz方法求解,根据方程(19)(20),矩阵A以及B中元素aik和bik的表达式可以写为以下形式:


图3 任意截面与矩形截面Fig.3 Arbitrary and rectangular sections
引入第一格林(Green)公式的二维形式:

式中:S=Sw+Sf,u与 v为封闭区域 Ω内连续可微的函数。将方程(26)应用于矩形计算域Ω0,并设u=φi,v=φk代入式(26),并利用边界条件(8)和(9)得:

考虑到指标i和k具有可交换性,由式(27)可知,函数φi在自由表面Sf0上具有如下的正交性:

再次利用第一格林公式(26)并考虑边界条件(8)(9)可以得到:

利用式(27)~(29),式(25)可以重新写为以下形式:

其中
由方程(30)可以看出,对于具有任意形状的液体区域Ω,采用Ritz方法求解晃动模态时,可统一采用矩形区域(截面)的基函数(式(22))进行求解,其广义特征值矩阵的系数可按式(30)计算,从而避免了针对不同截面(由于边界条件的不同)需分别构造基函数的复杂性。
4 数值算例
4.1 半顶角为45°的三角形截面
文献[2]给出了半顶角为45°的三角形渠道内流体晃动频率的近似解析解。截面尺寸如图4所示,其中水深为H,自由液面的半宽值为a,容器侧壁间半顶角θ为 45°。

图4 半顶角为45°的三角形截面渠道Fig 4.Canal with 45°-walls
选取式(22)为Ritz方法的基函数(取150项),矩阵A与B的系数按式(30)计算,应用Ritz方法得到归一化的一阶反对称以及正对称频率分别为1.019 0、1.574 2。文献[2]给出的近似解分别为1.000 0、1.524 4。本文 Ritz解答与文献[2]的近似解最大相对误差约3%,两者吻合良好。
4.2 半椭圆截面
选取文献[8]半椭圆截面液体作为计算实例,半椭圆容器无盖板及有盖板的的几何尺寸如图5所示。液体所占体积为容器容量的一半,符号a′,b′,L分别表示椭圆的半长轴、半短轴以及盖板长度。符号a则是自由液面静止时的半宽值。对于无盖板的椭圆容器,盖板长度L为零。
同样选取式(22)为Ritz方法的基函数,矩阵A与B的系数按式(30)计算。

图5 有盖板以及无盖板的半椭圆截面Fig.5 Baffled and un-baffled half elliptical sections
本文Ritz方法(基函数所取项数m为23)计算的前三阶反对称及正对称正规化的晃动频率与文献[8]保角映射方法的结果都列于表1,通过比较发现,本文和文献[8]结果的最大相对误差约为1%,由于正规化频率为频率平方的倍数,且本文结果与文献[8]的结果很接近,所以实际频率的最大相对误差大约为0.5%,两者结果吻合很好。
为了考察此时Ritz方法的收敛性,取两个无盖板的半椭圆截面为例,截面尺寸分别为a′=1.0 m,b′=0.1 m及 a′=1.0 m,b′=0.8 m,短长轴的比值分别为b′/a′=0.1,0.8。图 6、7分别显示了二个半椭圆容器内流体前3阶反对称与对称晃动频率随基函数项数m变化的图线,由图可见,对于本算例而言,Ritz方法收敛很快,只需取5~6项即可获得较高的计算精度,可满足工程使用要求。
通常情况下,采用本文Ritz方法计算,取较多的基函数项数可获得较高的计算精度,实际计算中可根据所要求的计算精度来确定取多少项。
需要说明的是,文献[8]的方法仅适用于半椭圆形状,而本文方法不仅适用于半椭圆截面的频率计算,同样适用具有任意液深的椭圆截面容器。
表1 前三阶正规化的反对称以及正对称晃动频率Tab.1 The first three normalized anti-symmetric and symmetric sloshing frequencies Ωj=g(j=1,2,3)
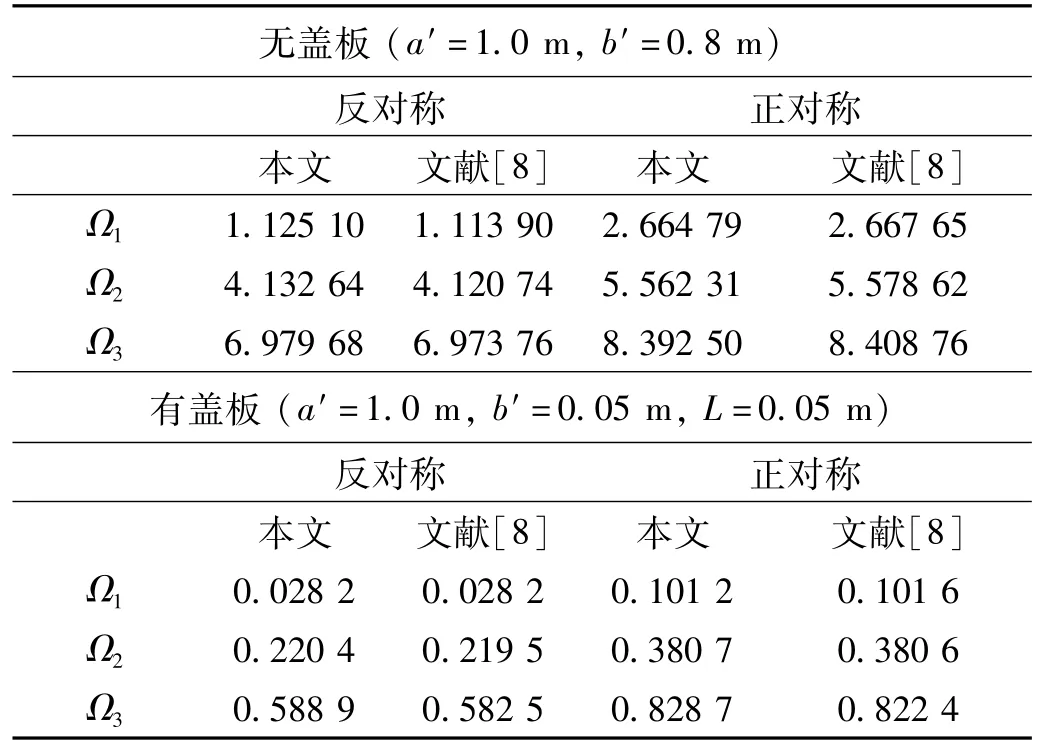
表1 前三阶正规化的反对称以及正对称晃动频率Tab.1 The first three normalized anti-symmetric and symmetric sloshing frequencies Ωj=g(j=1,2,3)
无盖板 (a′=1.0 m,b′=0.8 m)反对称 正对称本文 文献[8] 本文 文献[8]Ω1 1.125 10 1.113 90 2.664 79 2.667 65 Ω2 4.132 64 4.120 74 5.562 31 5.578 62 Ω3 6.979 68 6.973 76 8.392 50 8.408 76有盖板 (a′=1.0 m,b′=0.05 m,L=0.05 m)反对称 正对称本文 文献[8] 本文 文献[8]Ω1 0.028 2 0.028 2 0.101 2 0.101 6 Ω2 0.220 4 0.219 5 0.380 7 0.380 6 Ω3 0.588 9 0.582 5 0.828 7 0.822 4

图6 半椭圆 a′=1.0 m,b′=0.1 m频率收敛图线Fig 6.Convergence curves of frequencies(half elliptical section a′=1.0 m,b′=0.1 m)

图7 半椭圆 a′=1.0 m,b′=0.8 m频率收敛图线Fig.7 Convergence curves of frequencies(half elliptical section a′=1.0 m,b′=0.8)
5 结 论
基于Ritz方法,本文引入Green公式,将矩形截面晃动模态的精确解作为基函数,针对任意二维截面形状,建立了特征值问题Ritz求解方法的统一计算格式,避免不同截面(由于边界条件的不同)需要引入不同基函数的复杂性,使得Ritz方法在理论上适用于任意截面的二维晃动模态分析,可同时得到模态频率与振型解答,采用本文方法对半顶角为45°的三角形、半椭圆形截面的晃动模态进行求解,本文计算结果与其它解析方法的结果吻合良好,其计算精度完全满足工程要求。
[1]Dodge F T.The New Dynamic Behavior of Liquids in Moving Containers[R].Southwest Research Institute,San Antonio,TX,2000.
[2]Ibrahim R A. Liquid sloshing dynamics: theory and applications,[M].Cambridge:Cambridge University Press,2005.
[3]Faltinsen O M,Timokha A N.Sloshing[M].Cambridge:Cambridge University Press,2009.
[4]Lawrence H R,Wang C J,Reddy R B.Variational solution of fuel sloshing modes jet propulsion,1958,28(11):728-736.
[5]Lukovsky L A.Variational methods of solving dynamic problems for fluid-containing bodies[J]. International Applied Mechanics,2004,40(10):1092-1128.
[6]Budiansky B.Sloshing of liquids in circular canals and spherical tanks[J].Journal of Aerospace Sciences,1960,27(3):161-173.
[7]Fox D W,Kuttler J R.Sloshing frequencies,zeitschrift für angewandte mathematik und physik ZAMP,1983,34(5),668-696.
[8]Hasheminejad SM,Aghabeigi M.Liquid sloshing in half-full horizontal elliptical tanks[J]. Journal of Sound and Vibration,2009,324(1-2):332-349.
[9]Mciver P.Sloshing frequencies for cylindrical and spherical containers filled to an arbitrary depth[J].Journal of Fluid Mechanics,1989,201:243-257.
[10]周叮.截面任意形状的柱形和环形容器内液体晃动特性的精确解法[J].工程力学,1995,12(2):58-64.ZHOU Ding.An exact solution of liquid sloshing in cylindrical and annular tanks with arbitrary cross-sections[J].Engineering Mechanics,1995,12(2):58-64.
[11]Ibrahim R A,Pilipchuk V N,Ikeda T.Recent advances in liquid sloshing dynamics[J].Applied Mechanics Reviews,2001,54(2):133-199.
[12]Moiseev N N,Petrov A A.The calculation of free oscillations of a liquid in a motionless container[J].Advances in Applied Mechanics,1966,9:91-154.
[13]Ohayon R,Morand J P.Fluid-structure interaction:applied numerical methods[M]. New York: John Wiley &Sons,1995.
[14]Li Y,Wang Z.An approximate analytical solution of sloshing frequencies for a liquid in various shape aqueducts[J].Shock and Vibration,http:11dx.doi.org/10.1155/2014.672648

