二次函数在高考的考点
聂炜艺
二次函数是初中所学的知识,但高中继续深入学习,在高考中经常涉及,是中学阶段的一个重要函数.通常要求学生掌握二次函数的概念、解析式、图像及性质,能利用二次函数研究一元二次方程的实根分布条件,能求二次函数的区间最值.
一般来说,高考所出的题型包括以下三类:
1.求二次函数的解析式
例1 已知二次函数的对称轴为x=-2,截x轴上的弦长为4,且过点(0,-1),求函数的解析式.
解 ∵二次函数的对称轴为x=-2,
设所求函数为f(x)=a(x+2)2+b,
又∵f(x)截x轴上的弦长为4,
∴f(x)过点(-2+2,0).
f(x)又过点(0,-1),
∴4a+b=0,
2a+b=-1,a=12,
b=-2.
∴f(x)=12(x+2)2-2.
总结:求二次函数的解析式时,要根据条件选择不同的形式.
2.讨论二次函数的区间根的分布
这类问题的情况比较多,在考试时很少单独出题,数形结合是处理本类题目的重要思想方法.
例2 已知函数f(x)=x2-(2a-1)x+a2-2与非负x轴至少有一个交点,求a的取值范围.
解法一 由题知关于x的方程x2-(2a-1)x+a2-2=0至少有一个非负实根,设根为x1,x2,
则x1x2≤0或Δ≥0
x1x2>0
x1+x2>0,得-2≤a≤94.
解法二 由题知f(0)≤0或f(0)>0
--(2a-1)2>0
Δ≥0,得
-2≤a≤94.
总结:二次函数的区间根的分布情况一般需从三方面考虑:①判别式;②区间端点的函数值的符号;③对称轴与区间的相对位置.
3.讨论二次函数的区间单调性与最值问题
例3 函数y=x2+bx+c (x∈[0,+∞))是单调函数的充要条件是( ).
A.b≥0 B.b≤0 C.b>0 D.b<0
分析 对称轴x=-b2.
∵函数y=x2+bx+c(x∈[0,+∞)是单调函数,
∴对称轴x=-b2在区间[0,+∞)的左边,即-b2≤0,得b≥0.
因此选A.
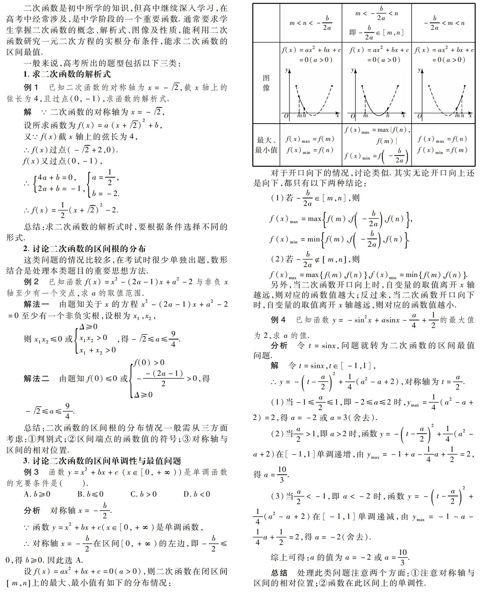
设f(x)=ax2+bx+c=0(a>0),则二次函数在闭区间m,n上的最大、最小值有如下的分布情况:
m m<-b2a 即-b2a∈[m,n] -b2a 圖 像f(x)=ax2+bx+c =0(a>0) f(x)=ax2+bx+c =0(a>0) f(x)=ax2+bx+c =0(a>0) 最大、 最小值f(x)max=f(m) f(x)min=f(n) f(x)max=max{f(n), f(m)} f(x)min=f-b2a f(x)max=f(n) f(x)min=f(m) 对于开口向下的情况,讨论类似.其实无论开口向上还是向下,都只有以下两种结论: (1)若-b2a∈[m,n],则 f(x)max=maxf(m),f-b2a,f(n), f(x)min=minf(m),f-b2a,f(n). (2)若-b2am,n,则 f(x)max=maxf(m),f(n),f(x)min=minf(m),f(n). 另外,当二次函数开口向上时,自变量的取值离开x轴越远,则对应的函数值越大;反过来,当二次函数开口向下时,自变量的取值离开x轴越远,则对应的函数值越小. 例4 已知函数y=-sin2x+asinx-a4+12的最大值为2,求a的值. 分析 令t=sinx,问题就转为二次函数的区间最值问题. 解 令t=sinx,t∈[-1,1], ∴y=-t-a22+14(a2-a+2),对称轴为t=a2. (1)当-1≤a2≤1,即-2≤a≤2时,ymax=14(a2-a+2)=2,得a=-2或a=3(舍去). (2)当a2>1,即a>2时,函数y=-t-a22+14(a2-a+2)在[-1,1]单调递增, 由ymax=-1+a-14a+12=2,得a=103. (3)当a2<-1,即a<-2时,函数y=-t-a22+14(a2-a+2)在[-1,1]单调递减, 由ymax=-1-a-14a+12=2,得a=-2(舍去). 综上可得:a的值为a=-2或a=103. 总结 处理此类问题注意两个方面:①注意对称轴与区间的相对位置;②函数在此区间上的单调性.

