基于分解的多目标进化算法在工程优化中的应用

张春江，TAN Kay Chen，高 亮，吴 擎

(1．华中科技大学 机械科学与工程学院，湖北 武汉430074;2．Department of Electrical and Computer Engineering，National University of Singapore，Singapore 117583;3． 华中农业大学 工学院，湖北 武汉430070)

0 引言

多目标优化问题(Multi-Objective Optimization Problems，MOPs)普遍存在于工程应用与科学研究中，这些问题的各个目标往往相互冲突，在对其优化时，需要对各个目标进行折衷处理． MOPs 往往没有唯一的全局最优解，而有一个Pareto 最优解集(Pareto Optimal Set，POS)． 采用传统的数学规划方法求解MOPs 时，如权重法、目标规划法等，一次运行只能求得一个解，而多目标进化算法(Multi-Objective Evolutionary Algorithm，MOEA)因其内在的并行性，能一次性求得一组Pareto 最优解．自从Schatter 和David［1］在1985 年首次提出用于多目标优化的向量评估遗传算法(Vector Evaluated Genetic Algorithm)以来，MOEA 得到了学者的广泛关注． 同时，许多学者提出了优秀的MOEA 算 法，如Zitzler 等［2］提 出 了SAPE-II;Deb［3］提出了NSGA-II;Bader 和Zitzler［4］提出了基于评估指标的HypE;2007 年Zhang 等［5］提出了一种全新的基于分解的MOEA 算法(Multi-Objective Evolutionary Algorithm based on Decomposition，MOEA/D)． 该算法结合传统的数学规划法，首先将多目标优化问题转发为众多单目标优化问题，然后采用进化算子同时优化这些单目标优化问题，最终获得一组Pareto 最优解． 与大多数MOEA 算法相比，MOEA/D 被证明有更快的求解速度，能获得分布性及收敛性更好的解集． 在2009 年的IEEE 进化计算大会中的多目标优化竞赛中，MOEA/D 荣获了第一名［6］．近年来，许多学者对MOEA/D 做出了很多改进，例如，Palmers等［7］让MOEA/D 分解的每个子问题记录多个解;Qi 等［8］为MOEA/D 提出了一种自适应权重调整方法;Li 等［9］为MOEA/D 提出了一种自适应算子选择方法;周爱民等［10］提出了一种基于混合高斯模型的MOEA/D． 目前，该算法也被成功应用于天线设计［11］、电力系统经济调配［12］、复杂网络聚类［13］、无线传感网络优化［14］等应用领域．

多目标优化标准测试问题的Pareto 最优前沿(Pareto Optimal Front，POF)的各目标值往往在［0，1］区间，MOEA/D 在这些问题上表现良好．但现实中的工程优化问题各目标函数往往有不同的单位量度，并且其函数值常在不同的数量级上．当直接应用MOEA/D 求解时，会造成极差的解集分布性［12］，因此，需对各目标函数进行归一化处理．Zhang 等［5］利用当前种群的信息来归一化，但该方法使得原目标函数动态变化，并在某些目标难以优化的情况下，该方法也会失效． Zhu 等［12］采用目标函数的最大和最小值来归一化，在某些情况下，该方法不适合MOEA/D．

笔者旨在提供一种新的归一化方法，以便将MOEA/D 应用于工程优化问题． 另外，笔者采用一种自适应ε 约束处理方法来处理工程优化问题中的约束．

1 问题定义

不失一般性，工程优化中的多目标优化问题通常可以采用以下数学模型加以定义:

该问题有m 个优化目标，决策向量X =(x1，x2，…，xn)，有k 个不等式约束及l 个等式约束，最大化问题可采用下式转化为最小化问题．

max fi(X)= -min(-fi(X))． (2)

1．1 Pareto 最优解

MOPs 中的最优解通常被称为Pareto 最优解(Pareto Optimal Solution)． 对于式(1)中的MOP，其Pareto 最优解X*定义如下:对于X*∈Ω(表示满足(1)中所有约束的可行集)，如果不存在其他任何X'∈Ω 使得fj(X*)≥fj(X')(j =1，2，…，m)同时成立，且至少有一个严格不等式成立，则称X*是min f(X)的Pareto 最优解．

1．2 Pareto 最优解集

MOPs 的Pareto 最优解往往不止一个，而存在一组相互制约的最优解集，被称为Pareto 最优解集，其定义如下:

Pareto 最优解集是所有Pareto 最优解的集合．

1．3 Pareto 最优前沿

Pareto 最优前沿是Pareto 最优解集在目标函数空间的映射，定义如式(4)所示:

2 基于分解的多目标进化算法(MOEA/D)

MOEA/D 是一种全新的多目标优化框架，在该框架中，多目标优化问题被转化为一系列单目标优化子问题，然后利用一定数量相邻问题的信息，采用进化算法对这些子问题同时进行优化，因为每一个单目标优化问题的最优解对应于Pareto最优前沿上的一个解，最终能求得一组Pareto 最优解．由于分解操作的存在，该方法在保持解的分散性方面有着很大优势，而通过分析相邻问题的信息来优化，能避免陷入局部最优．与NSGA-II 相比，MOEA/D 能在更快时间内获得分散性更好并更精确的Pareto 近优解集［5］．

较为常用的分解策略是切比雪夫(Tchebycheff)分解法．该方法对Pareto 最优前沿的形状不敏感．笔者也采用该策略将MOP 问题min f(X)转化为min(Xλj，z*)，j=1，2，…，N，如下式所示:

式中:λj= (，…，)T，为相应的权重向量，并满足条件，0 ≤≤1，∑= 1，λj的设定算法见文献［5］;z*=，…)T为参考点，=min{fi(X)}． 可以证明，每一个子问题的最优解都是MOP 的Pareto 最优解，且MOP 的每一个Pareto 最优解都对应一个切比雪夫子问题．

3 归一化方法

MOEA/D 适用于求解各目标函数的范围和量纲一致的问题．将MOEA/D 直接应用于各目标值量纲和数量级不同的工程优化问题时，目标函数会向着数值较大的目标进化，往往只能获得分散性较差的Pareto 近优前沿，因而需要归一化处理．Zhu 等［12］在采用MOEA/D 优化电力环境经济调度问题时，采用以下方法进行归一化．

式中:ftransi表示归一化后的第i 个目标函数;fi表示原始的第i 个目标函数值和分别表示第i 个目标函数的最小值和最大值．有时某个会非常大，甚至存在并不存在的情况，这时候该归一化方法就会失效．

对于MOEA/D，最理想的归一化方法如下所示:

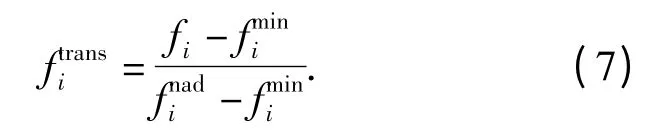
Zhang 等［5］认为很难求解fmin和fnad，并提出了一种自适应归一化方法，如式(9)所示:

笔者将采用式(7)的方法来进行归一化． 现在的问题便转化为了怎样求fmin和fnad．对于MOP存在以下定理:在一般情况下，对于有m 个目标的MOP，它的Pareto 最优解无论在解空间还是目标空间都是一个分段连续的m -1 维流形． 这说明，当m =2(双目标优化问题)时，pareto 最优前沿是一个分段连续的一维流形，一般情形下是一条一维曲线，显然，恰好是曲线的两个端点．

对于双目标优化问题，采用以下方法来求解fmin和fnad． 首先，采用一种高效的约束优化算法，即自适应εDE［16］分别优化f1和f2而求得和．要求解和，只需采用自适应εDE 求解式(10)和式(11)，可证明这两式的最优值为和．式(11)最优解的示意图如图1 所示．约束条件f1(X)实际上只能取到f1(X)=，如图中的虚线所示．在这虚线上，f2能取到的最小值只能是当虚线与Pareto 前沿相交时取到该最小值，此交点也是Pareto 前沿的一个端点．

与公式(9)相比，公式(6)和公式(7)的方法要先求解归一化所需的fmin和fmax或fnad． 但因为单目标优化的计算复杂度要低于多目标优化，并且单目标优化所需的种群大小也一般小于多目标优化．另外，当采用公式(6)和公式(9)进行归一化时，不需要更新z*，可节约计算时间．因而采用公式(6)和公式(9)的方法并不会增加额外的计算时间，甚至比公式(7)的方法所需时间更少．

图1 式(11)的最优解示意图Fig．1 Illustration of optimal solution for formula (11)

4 自适应ε 约束处理及自适应ε 差分进化算法

ε 约束处理方法最先由Takahama 等［17］提出．该方法用来比较两个候选解的优劣．在该方法中，存在一个ε 值，当两个解的约束违反量都小于ε 时，则根据目标函数值的大小来比较，否则采用违反约束的程度来比较．数学表达式如下:

其中，φ 表示约束违反量，计算方式如下:

式中:δ 为等式约束的容许误差值．

Takahama 和Sakai 将ε 约束法与差分进化算法相结合，赢得了2006 年与2010 年IEEE 计算智能大会上约束优化竞赛上的第一名［18-19］．笔者采用Zhang 等改进的自适应ε 约束法． Zhang 等［16］利用当前种群中的信息而采用一种自适应方式来控制ε 值．具体控制方法如式(14)所示:

式中:t 表示迭代次数;φmax表示种群中约束违反量的最大值;φ0表示种群中约束违反量为0 的个体数;N 表示种群大小;Tc 表示迭代次数的阈值;Th 也是阈值;ap1和ap2是介于0 和1 之间的系数．上式表示，当种群中φmax很大或者可行解很多时，直接让ε 取0;否则，让ε 取值为φmax的ap2倍．

DE 算法由Storn 和Price［20］提出．Zhang 等人将自适应ε 约束方法与最简单的一种DE 算法(DE/rand/1/exp)结合．数值试验证明，该方法具有求解速度快、精度高、鲁棒性强等优点．用来求解fnad的εDE 算法的伪代码如图2 所示．

5 算法步骤

将MOEA/D 应用于工程优化问题的具体步骤如下:

(1)参数设置． 设置自适应εDE 算法的参数以及MOEA/D 的参数．

(2)采用自适应εDE 算法求解fmin和fnad．

(3)初始化MOEA/D． ①初始化权重向量λ1，…，λN，具体方法见参考文献［5］，计算这些权重向量之间的欧氏距离，为每个权重向量找出T个与其距离最近的向量，从而构成B(i)={i1，…，iT};②采用均匀分布在定义域中生成种群大小为N 的种群X，并计算初始种群的目标函数与约束违反量;③迭代次数初始化:Gen=0．

图2 自适应εDE 的伪代码Fig．2 Pseudo-code of adaptive εDE

(4)算法迭代更新．

a)根据式(14)定义ε 值．对每一个个体i，进行如下操作．

b)根据下式选择重组父本的范围:

其中，rand 为服从均匀［0，1］分布的随机数．

c)重组．令r1=i，从P 中随机选择r2和r3．根据DE 算子重组出新解=(，…，)． 每一维如下式所示:

其中，F 和CR 是两个参数．再通过一个多项式突变算子得到解Y．具体见文献［15］．

d)修复． 如果新解Y 的某个元素值超出边界，则赋予该元素一个边界内随机值．计算新解Y的函数值f(Y)及约束违反量φ(Y)．

(5)终止准则． 如果迭代次数gen =Genmax，则停止迭代，输出结果;否则，gen =gen +1，并返回步骤(4)．

6 数值实验

为了验证笔者提出归一化方法的有效性，选取了另两种方法来进行对比，这两种方法分别采取公式(6)和公式(9)来归一化． 首先选用CEC2009 中多目标优化竞赛［21］中的一个问题CF6 来比较3 种归一化方法．

6．1 CF6 测试问题

对于CF6，CEC2009 的标准测试问题的最大函数评估次数为300 000，种群大小为600，最大迭代次数为500，其他参数的设置请参考文献［15］．在求解fmin、fnad和fmax时，种群大小设置为40，最大迭代次数设置为2 000，其他参数设置请参考文献［16］．

CF6 的两个目标函数范围都在［0，1］，本不需要归一化，因此，将原目标函数f1乘以10，经改造的CF6 如下所示:

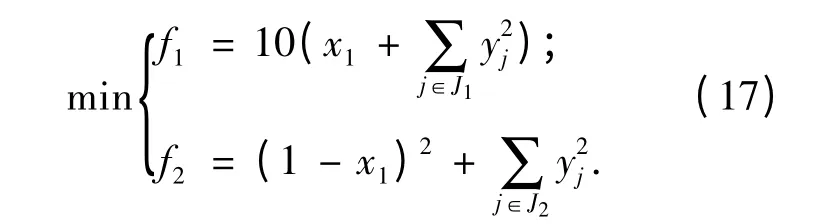
其中，J1=j 是奇数且2≤j≤n}，J2=j 是偶数且2≤j≤n}，且

约束条件为

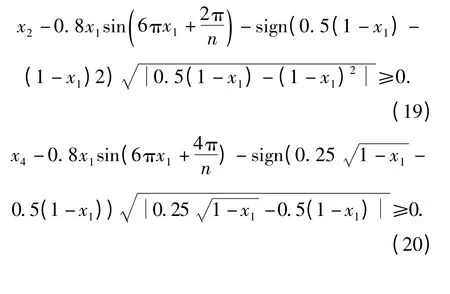
决策空间为［0，1］×［-2，2］n-1．

采用公式(6)的归一化方法，需要先求fmin和fmax．这里采用自适应εDE 算法来求解，求得fmin=［0，0］，fmax=［270．9，30．9］． 采用本文方法，也就是公式(7)的方法，需要求fnad，求得fnad=［10，1］．对于公式(6)的方法，可以先根据式(8)计算fTnad=．因为与相差不大，因此，可以推断公式(6)的方法与本文方法效果相当．3 种方法均采用相同的算法参数，最终求得的解如图3 所示．

图3 对CF6 各方法Pareto 前沿的比较Fig．3 Pareto fronts of different methods for CF6

图3 中第一个子图为真实的Pareto 前沿．3种方法都没有求得f2的范围在［0，0．2］的Pareto最优前沿．公式(6)的方法与本文方法相当，这是因为采用公式(6)时，该问题的fTnad1与fTnad2相差不大;公式(9)的方法结果较差，其一为分散性较差，f2的范围在［0．4，1］的Pareto 前沿非常稀疏，原因在于此问题比较难于优化． 在优化后期该问题的z*约为［0，0．2］，(种群中的最大目标函数值)约为［110，1］． 此时，计算fTnad为，可见远大于，因此导致了较差的解集分布性． 公式(9)的结果较差还表现在精度不高． 从图3(c)可见，公式(9)方法所获的前沿不光滑，有些解不是非支配解，这是因为采用公式(9)的方法使子问题变成了动态优化问题，收敛速度变慢了．

对于该问题，采用自适应εDE 求解fmin时，可获得fmin=［0，0］．但采用MOEA/D 进行求解时，却无法求得f2的范围在［0，0．2］的Pareto 最优前沿．在已知fmin=［0，0］和fnad=［10，1］的情况下，可以结合归一化方法让更多的解集中在f2的范围为［0，0．2］的Pareto 最优前沿处． 具体方法是在归一化时加大fnad1． 比如，当分别采用fnad=［20，1］和［100，1］进行归一化时，可获得如图4所示的最优前沿． 很显然，当fnad1 增加的越大时，对Pareto 前沿的下端的优化就越集中，因而图4中右图Pareto 前沿的下端要优于左图，而上端却较左图稀疏．

图4 增加fnad1 时所获得Pareto 前沿Fig．4 Pareto fronts obtained by increasing

下面选取逆向世代距离(Inverted Generation Distance，IGD)进一步比较这几种方法． IGD 的定义如下式所示:

分别采用公式(6)、公式(9)、公式(7)以及采用公式(7)时将增大为100 来归一化处理，将算法随机运行30 遍．IGD 的平均值与标准差及每种方法所需的平均运行时间如表1 所示． 每种方法获得IGD 做出箱线图如图5 所示．

由表1 和图5 可知，采用公式(9)的归一化方法所获的IGD 最大，公式(6)和公式(7)的方法没有明显的差异，这与之前分析是一致的．相对而言，公式(7)方法所获的解IGD 更集中，而采用公式(7)方法时，将fnad1 增大为100 能明显提高算法的性能，不但能获得更小的IGD 值，并且比其他方法更加集中． 这就是因为当fnad1 =100 时，会有大量的解集中到难以优化的Pareto 前沿附近，因而能跳出该处的局部最优，获得更为完整Pareto最优前沿，结果如图4 所示．

表1 4 种方法对CF6 运行30 次求得的IGD平均值、标准差及所需平均时间Tab．1 IGD’s average value，standard error and average time by the four methods running 30 times for CF6

图5 4 种方法对CF6 运行30 次的IGD 的箱线图Fig．5 Boxplot of four methods for CF6

由表1 可见，虽然需要先计算归一化所需的fmin和fmax或fnad，但公式(6)和公式(7)不需要更新z*，所以这两种方法反而比公式(9)的方法的计算时间更少．

作出IGD 为中位数时各方法的IGD 收敛曲线如图6 所示． 可见，公式(9)的方法最差，波动也较大，这正是fnad和z*不断变化的结果．采用公式(6)和公式(7)求得的IGD 非常接近．而采用公式(7)并将增大为100 时，能收敛到更低的IGD 值，这是因为有更多的解集中到Pareto 前沿的下端，而能跳出局部最优．

图6 4 种方法求解CF6 的IGD 收敛图Fig．6 IGD’s converge plots of four algorithms for CF6

6．2 焊接梁设计问题

笔者选用焊接梁设计问题［22］验证该算法的有效性，其目标是最小化制造成本和末端挠度，其约束为在一定的负载下剪切应力和弯曲应力均满足要求．

对于该问题，种群大小设置为100，最大迭代次数为100;自适应εDE 的种群大小为20，最大迭代次数为500．

用自适应εDE 算法求的fmin=［1． 861 6，0．000 44］，fmax=［1 220，0．071 28］，求得fnad=［35．23，0．015 7］．对于公式(6)的方法，计算其fTnad=［0．027，0．215］，可见两个值相差较大． 采用3 种方法所获得的Pareto 前沿如图7 所示．

从图7 可见，该问题的Pareto 最优前沿有比较陡峭的尖端和很平缓的尾端． 当采用MOEA/D求解时，所获的解在尖端和尾端非常稀疏．对于此问题，结合本文的归一化方法提供一种解决思路．对于同一个问题采用两个种群分别求解，对一个种群归一化时增加，对另一个种群归一化时增加，最后所得解合二为一，就能得到在整个Pareto 最优前沿上都分布较好的解． 这里每个种群采用50 个粒子，分别将和扩大10 倍，最终分别获得的Pareto 前沿以及混合后的Pareto 前沿如图8 所示．

图7 对焊接梁设计问题各方法Pareto 前沿的比较Fig．7 Pareto Fronts obtained by three methods for weld bean design

7 结束语

为了将MOEA/D 算法更好地应用于各目标数量及量纲不同的多目标优化问题，笔者提出了一种新的归一化方法，并采用了一种自适应ε 约束处理方法来处理约束． 归一化方法采用一种自适应εDE 算法来求解归一化所需的fmin和fnad．通过数值实例，证明了该方法能获得分布性较好的Pareto 前沿，并且该方法能克服其他两种归一化方法的缺点．另外，通过灵活运用该归一化方法，MOEA/D 能对Pareto 前沿的一端集中优化，因而能处理一些Pareto 前沿的两端比较难以优化的多目标优化问题．

［1］ SCHAFFER，DAVID J． Some experiments in machine learning using vector evaluated genetic algorithms［D］． Nashville，TN (USA):Vanderbilt Univ，1985．

［2］ ZITZLER E，LAUMANNS M，THIELE L． SPEA2:Improving the strength pareto evolutionary algorithm for multiobjective optimization［R］．Zurich:Computer Engineering and Networks Laboratory(TIK)，Swiss Federal Institute of Technology(ETH)，2001:19-21．

［3］ DEB K，PRATAP A，AGARWAL S，et al． A fast and elitist multiobjective genetic algorithm:NSGA - II［J］． IEEE Transactions on Evolutionary Computation，2002，6(2):182 -197．

［4］ BADER J，ZITZLER E． HypE:An algorithm for fast hypervolume-based many-objective optimization［J］．Evolutionary Computation，2011，19(1):45 -76．

［5］ ZHANG Qingfu，LI Hui． MOEA/D:A multiobjective evolutionary algorithm based on decomposition ［J］．IEEE Transactions on Evolutionary Computation，2007，11(6):712 -731．

［6］ ZHANG Qingfu，LIU Wudong，LI Hui． The performance of a new version of MOEA/D on CEC09 unconstrained MOP test instances［C］//In IEEE Congress on Evolutionary Computation． Trondheim:IEEE Press 2009:203 -208．

［7］ PALMERS P，MCCONAGHY T，STEYAERT M，et al． Massively multitopology sizing of analog integrated circuits［C］//Conference on Design，Automation and Test in Europe，DATE 2009．Nice:IEEE Press，2009:706 -711．

［8］ QI Yutao，MA Xiaoliang，LIU Fang，et al． MOEA/D with adaptive weight adjustment ［J］． Evolutionary computation，2014，22(2)，231 -264．

［9］ LI Ke，FIALHO A，KWONG S，et al． Adaptive operator selection with bandits for a multiobjective evolutionary algorithm based on decomposition［J］． IEEE Transactions on Evolutionary Computation，2014，18(1):114 -130．

［10］周爱民，张青富，张桂戌． 一种基于混合高斯模型的多目标进化算法［J］． 软件学报，2014，25 (5):913 -928．

［11］CARVALHO R D． A multi-objective evolutionary algorithm based on decomposition for optimal design of Yagi-Uda antennas［J］． IEEE Transactions on Magnetics，2012，48(2):803 -806．

［12］ ZHU Yongsheng，WANG Jie，QU Boyang． Multi-objective economic emission dispatch considering wind power using evolutionary algorithm based on decomposition［J］． International Journal of Electrical Power ＆Energy Systems，2014，63:434 -445．

［13］ GONG Maoguo，CAI Qing，CHEN Xiaowei，et al．Complex network clustering by multiobjective discrete particle swarm optimization based on decomposition［J］． IEEE Transactions on Evolutionary Computation，2014，18(1):82 -97．

［14］ KONSTANTINIDIS A，YANG K． Multi-objective energy-efficient dense deployment in wireless sensor networks using a hybrid problem-specific MOEA/D［J］．Applied Soft Computing，2011，11(6):4117 -4134．

［15］ LI Hui，ZHANG Qingfu． Multiobjective optimization problems with complicated Pareto sets，MOEA/D and NSGA-II ［J］． IEEE Transactions on Evolutionary Computation，2009，13(2):284 -302．

［16］ZHANG Chunjiang，LIN Qun，GAO Liang． A novel adaptive ε-constrained method for constrained problem［C］//In Proceedings of the 18th Asia Pacific Symposium on Intelligent and Evolutionary Systems． Singapore:Springer，2015:573 -586．

［17］ TAKAHAMA T，SAKAI S，IWANE N． Constrained optimization by the epsilon constrained hybrid algorithm of particle swarm optimization and genetic algorithm［C］//Ai 2005:Advances in Artificial Intelligence．Sydney，Australia:Springer，2005:389 -400．

［18］TAKAHAMA T，SAKAI S． Constrained optimization by the epsilon constrained differential evolution with gradient-based mutation and feasible elites［C］//IEEE Congress on Evolutionary Computation．Ancouver，BC:IEEE Press，2006:1-8．

［19］ TAKAHAMA T，SAKAI S． Constrained optimization by the ε constrained differential evolution with an Archive and gradient-based mutation ［C］//2010 IEEE Congress on Evolutionary Computation (CEC)．Barce:IEEE Press，2010:25 -32．

［20］ STORN R，PRICE K． Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces［J］． Journal of Global Optimization，1997，11(4):341 -359．

［21］ ZHANG Qingfu，ZHOU Aimin，ZHAO Shizheng，et al． Multiobjective optimization test instances for the CEC 2009 special session and competition［R］． University of Essex，Colchester，UK and Nanyang Technological University，Singapore，2008:1 -30．

［22］RAY T，TAI K． An evolutionary algorithm with a multilevel pairing strategy for single and multiobjective optimization［J］． Foundations of Computing and Decision Sciences，2001，26(1):75 -98．