基于建模驱动的经管类专业图论教学探究

杨利峰，王先超，朱剑峰

(阜阳师范学院a.经济学院;b.数学与统计学院，安徽 阜阳 236041)

图论是运筹学课程的核心组成部分，其在商务管理、复杂系统、行为经济学和社交网络等经济、管理领域有着广泛的应用[1]。经管类专业学生认为图论中一些算法系统性较强，难懂且不知如何运用，提不起学习兴趣，而通过建模驱动的数学类课程教学能够在经管类学生中取得好的成效[2]。随着信息技术在社会生活等领域的逐步渗透，大数据时代的到来，数据复杂性也快速增长，其复杂性主要表现为多样性、低价值、实时性等[3]，基于复杂数据的图论教学更需与时俱进。所以在教学中应有效挖掘图论中潜在的思维模式，培养学生运用图的基本理论思考和解决实际问题的能力，全方位提高学生的综合素质[4]。为帮助学生掌握图论中经典算法的基本理论、思维模式，以便学生能够利用相关知识解决实际问题，将从现实生活中的图论问题，算法基本思想及步骤，建模驱动的实践等方面展示图论中Dijkstra 算法和Floyd 算法教学实践，然后对建模驱动的图论教学做了相应的思考。

1 图论中的实际问题

1.1 图论中的经典问题

哥尼斯堡七桥问题: 哥尼斯堡七桥问题是18世纪经典数学问题之一。有七座桥将哥尼斯堡城市中的两个岛和河岸连接起来，旅游者不禁要问是否存在一条路径经过七座桥一次且仅一次。1736年，欧拉在递交给圣彼得堡科学院的论文《哥尼斯堡七桥》中提出了欧拉定理，指出由于哥尼斯堡七桥问题中存在不止两个奇数度节点，所以不存在这样的道路，即不存在欧拉道路[5]。欧拉在解决哥尼斯堡七桥问题的同时开创了数学的一个重要分支——图论。

旅行推销员(TSP)问题:在N 个城镇间如何设计一条路线，使得推销员能够从其所在城镇出发经过其余城镇一次且仅一次，回到原城镇并满足所走行程最短。满足条件的路线称之为最佳推销员回路，寻找最佳推销员巡回相当于在加权完备图中寻找H 圈，即汉密尔顿回路。TSP 问题是一个组合优化问题，该问题被证明具有NP 计算复杂性，此后的一些导致该问题简化的方法都引起了广泛关注[6-7]。

四色问题: 四色猜想是数学的著名猜想之一，通常的说法为任一平面地图都可以用四种颜色来着色，且没有任何两个相邻的区域颜色相同。1976年，Appel 和Haken 借助计算机花了1200 小时，获得了1936 个构形的不可避免集，做了100 亿次判断，成功的进行了四色问题的证明[8]。四色问题的研究产生了新的数学理论，发展了数学计算技巧，且体现了图论基本理论与现代计算技术工具的完美结合[9]。

1.2 信息时代背景下的图论新问题

社交平台上的博客群问题:随着信息技术对社会经济生活的广泛渗透，图论也应用到网络舆情传播和政治群体的构建等社会管理方面，逐渐成为计算社会科学领域研究的重要工具，其对推动复杂、动态数据的分析有积极的意义。Blogosphere 博客空间的数据经过相应的计算得到了两大群体:自由派群体和保守派群体。在图1中节点表示不同派别个体对应的博客[10]。每个博客节点的大小反应了其与其他节点联接的程度。群体内博客的联接密度显著大于群体间博客的联接密度，两大群体间边缘个体的博客交往信息可以预测群体间边缘个体的政治倾向变化。

病毒式营销问题:商业营销和商务管理在大数据背景下也需要图的相关理论进行支撑[11]。文献[11]展示了在线社交网络中的病毒式营销模式，这种营销模式能够以较低的成本增加销售额。但是进行病毒式营销的关键问题是识别最具影响力的用户，以此类用户为信息扩散的核心进行营销信息扩散。这需要解决信息的时效性问题，在某一时刻定义孤立用户及用户信任程度等信息，再通过虚拟社交网络结构建立模型，然后以时间因素为主变量考虑病毒式营销的扩散动态过程。文献[11]中通过SNS 网站数据信息提取了一些个体在某一时刻的网络信任信息，如图2所示。

图1 政治博客群的结构

图2 某时刻用户间的信任网络

上述这些实际问题都与图论中最短路问题密切相关，下面介绍图论中最短路算法教学如何在实际问题建模驱动中进行。

2 图论教学中最短路算法的基本理论

最短路问题分为两类:单源最短路问题和全局最短路问题。这两类问题分别对应着两个经典的最短路算法:Dijkstra 算法和Floyd 算法。

2.1 最短路算法的基本思想

首先介绍一下上述两个经典算法的基本思想。

Dijkstra 算法的基本思想: 假设每个节点都有一对标号〈di，fi〉，其中di是从起点v0到节点vi的路径长度，fi表示节点vi的父节点的标号，用以确定路径。Dijkstra 算法就是通过不断比较插入可能的父节点后，更新节点标号，以致进行永久标号。这一永久标号过程就形如树生长，当所有节点都进行了永久标号后，就得到了以某一固定起点为根节点的树，也就确定了固定起点的最短路径。

Floyd 算法的基本思想: 在初始图的带权邻接矩阵中不断插入节点组合，依次构造新的距离矩阵D1，D2，…，DN，在构造新的距离矩阵的同时不断更新路径矩阵R1，R2，…，RN，最终得到的距离矩阵DN中元素表示了对应位置节点对间的最短距离。通过查找RN矩阵中的元素值就可以得到对应节点对间最短距离是通过怎样的路径走出的。

2.2 最短路算法的基本步骤

设G 为一赋权网络，权均非负，其邻接矩阵用W 表示。d(v) 表示距离标号，f(v) = v0表示父节点标号，w(v*，v) 表示邻接矩阵中两个节点之间的权数。Dijkstra 算法的主要步骤:

D(i，j) 表示具有n 个节点的图中节点vi和vj间的距离，r(i，j) 表示节点vi和vj间插入的节点标号，w(i，j) 表示邻接矩阵中的元素。Floyd 算法的主要步骤:

Step1:赋初值，∀i，j，d(i，j) ←w(i，j) ，r(i，j) ←j，k ←1 ;

Step2:若d(i，k) +d(k，j) ＜d(i，j) ，更新d(i，j) ，r(i，j) ，即d(i，j) ←d(i，k) + d(k，j) ，r(i，j)←k;

Step3:若k = n，停止，否则k ←k + 1 ，回到Step2。

3 基于建模驱动的最短路算法教学实践

3.1 问题建模驱动的实践教学一

实际问题: 微信社交网络平台应用十分广泛，如何评价自己与微信好友的联系的亲密程度?

问题分析:在现实的管理问题中需经常解决分类问题，这个问题实际上就是将某一同学朋友圈内的朋友分成若干群体，不同的群体表示不同的亲密度。在虚拟社交平台上，两个朋友间的亲密程度可以具象化地用他们之间联系的多少及频率来衡量，他们之间联系得多意味着他们之间的交往距离就短，否则就表示他们之间的交往距离较长。因此，可以用朋友圈内朋友与该同学之间的交往距离大小来进行亲密程度分类。这样该实际问题就化为了固定起点的最短路问题，即该问题可以用Dijkstra 来解决。

解决步骤:

Step1:某一学生将自身微信朋友圈的信息交流信息进行整理，得到两两朋友间的交流信息;

Step2:将交流信息进行距离化( 假设以交往信息条数的倒数作为距离，交往信息越多则距离越短)，得到初始的距离矩阵;

Step3:按照Dijkstra 算法的主要步骤，将初始距离矩阵带入，进行固定起点的最短路计算，并将朋友按照计算结果进行分成5 类( 非常亲密的朋友、亲密的朋友、较为亲密的朋友、联系较少的朋友和很少联系的朋友)。

下面介绍包含某一学生本身共计183 位成员，利用自身数据的解决结果。其将微信平台中一个月时间内的信息推送指向信息( 那个成员在推送，哪些成员在回应信息) 进行统计，在获取微信交流信息数据的基础上进行距离定义，再依据固定起点的最短路算法( Dijkstra 算法) 进行计算，并对计算后的数据进行可视化展示，结果如表1和图3所示。

表1 微信朋友圈的亲密程度等级划分结果

初始时刻的数据可视化信息及计算后的数据可视化信息如图3所示:

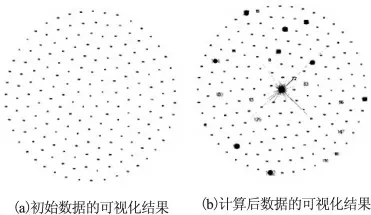
图3 微信朋友亲密程度数据的可视化结果

通过该学生将其微信朋友圈中信息推送信息的统计和计算，得到了其朋友圈亲密程度的划分。表1中其将朋友群体分为5 类: 非常亲密的朋友，，若亲密朋友，较为亲密的朋友，联系较少的朋友和很少联系的朋友，对应的成员个数分别为4，5，7，6 和160 个，通过这组数据可以发现，微信朋友圈中很多朋友都是很少联系的，很少联系的朋友比例约占总数的87.91%，说明该学生在社交网络中的活跃程度不是很高。在图3中，针对联系的密切程度对不同成员节点的大小进行了赋权，节点越大表明联系越紧密。

3.2 问题建模驱动的实践教学二

实际问题:同一宿舍的6 位学生之间的联系是否密切，宿舍舍友间是否存在小团体，这种小团体的成因是什么?

问题分析:同一宿舍6 个同学的群体划分问题实际上是对宿舍每一成员与他人间距离进行整体评价。在实际操作中，同宿舍成员间的交往频率往往不能实际统计，可以借助通讯和社交平台数据进行数据统计，其一定程度上也可以反映成员之间的交往多少。有了成员间交往的数据信息，可以通过合理的假设，设定成员间距离如何衡量，进而获得初始的成员间的距离矩阵。接下来的工作就是计算任意一对成员间的最短距离，然后再对每一成员与其他5 个成员间的整体距离进行判定，得到群体划分的直接依据。

解决步骤:

Step1:某一学生将自身通讯数据( 包括通话、短信信息、QQ 信息和微信信息)在某一时间内进行统计;

Step2:将通讯数据进行距离化( 同样可以假设以交往信息的条数的倒数作为距离，交往信息越多则距离越短)，得到初始的距离矩阵;

Step3:按照Floyd 算法的主要步骤，将初始距离矩阵带入，进行任意起点的最短路计算，得到任一对成员之间的距离(为使节点间边在图像显示中美观，将不同对成员间算出的距离进行了同比例的放大、取整，具体例子中距离数据调整后如表2所示)。

Step4:按照简单的算术平均，将每一成员与他人间的平均距离得到，若两个成员与其他成员间的平均距离值相差超过一定比例( 这里设定为100%)就视为他们不在同一个群体，进而得到群体的划分。

下面介绍某一学生利用其宿舍群体数据的解决结果。将同一宿舍6 位同学的手机通讯数据( 包括通话、短信信息、QQ 信息和微信信息) 进行为时2 月的统计，并利用任意起点的最短路算法( Floyd算法)进行计算和评价，将计算结果展示如下。

同宿舍6 位同学间距离的计算结果如表2。

表2 宿舍同学间距离计算结果

宿舍6 位同学根据距离设定阈值划分为3 个群体，数据可视化结果如图4。

图4 宿舍同学群体划分数据的可视化结果

通过表3的数据可以看出同学3 和其他同学间的联系最为紧密，而同学5 和同学6 和其他4 位同学的联系较少，距离较远。根据设定的阈值对同宿舍的6 位同学进行了群体划分，将6 位同学化为3 个群体，同学1 和同学6 各成为一个群体，同学2、同学3、同学4//同学5 成为了一个群体，这与该宿舍同学的切身感受基本一致。这6 位同学对宿舍形成的交往现状进行了思考，觉得同学1 和同学6 和其他4 位同学联系较少的原因是她们对自己的学习要求更为严格，非上课时间主要是在自习室和图书馆度过，造成了联系较少。

通过两个实际问题的驱动教学，学生不仅对最短路的两个经典算法有了深刻的了解，而且通过动手实践对自身的交往信息做了科学的计算，取得了对自身交往信息更为客观的认识和评价。这些实践对经管类学生利用综合知识对现实问题作出科学评价提供了有益的尝试。

4 建模驱动经管类专业图论教学的思考

4.1 建模驱动为图论教学带来开放性

传统图论教材中的教学内容、体系、模式有自我封闭的趋势，尤其是在大数据、复杂数据大发展的背景下，如何结合现实生活中新现象，提出新的具有吸引力的新问题，是引导经管类学生对图论等相关知识进行深入学习和实践的关键。大数据时代的到来不仅给网络科学的发展提供了新的动力和机遇，也为支持网络发展的基础理论之一的图论教学提供了建模驱动的契机。“众包”( 众包是种分布式问题解决模式，它将指定人员执行指定任务的方式变为了自由自愿接受任务的方式[13]) 这种网络科学理论的驱动模式在图论教学与实践中也应该有强大的生命力。类似于众包的建模驱动模式，拓展了学生对虚拟社交平台等新问题的认识，意识到了图论知识运用的广泛性及带来的趣味性，增强了学习兴趣。

4.2 建模驱动为图论教学带来融合性

学科交叉运用变的越来越普遍，大量实践交流平台中问题的解决需要图论知识与经管类其它专业知识的综合运用，经管类学生创新能力的培养离不开学科交叉运用能力的培养。随着社会经济发展，经管类专业学生需要面临的是分析更为复杂的问题，而以往的单一理论教学模式无法解决问题分析和学生创新能力培养的问题。一些实际问题驱动的学科竞赛平台中展示的问题需要图论与其他经管类知识的融合，如: 美国大学生数模竞赛出现了进行恐怖分子的社交网络分析此类与图论密切相关题目。2013 年全国数学建模竞赛题目“车道被占用对城市道路交通能力的影响”，2014 年数学建模美国赛中“高速公路交通规则的制定”及“体育功勋教练员贡献的评价”。上述问题中不仅需要学生有对实际问题进行分析和判断的能力，更需要学生综合运用图论与经济学、管理学、决策等理论来解决。

4.3 建模驱动为图论教学带来合作性

经管类学生培养的一个重要方面就是沟通能力、协调能力和组织能力的培养。在建模驱动的实际问题解决过程中，不论是问题分析，还是数据获得方式、数据收集及数据计算和评价都是复杂的，在复杂问题的解决中需要团队合作。建模驱动的教学模式要求学生成立学习小组，倡导学生间的合作，培养学生团队精神，团队精神能够促进团队成员的学习和创新等能力的培养。解决实际问题的过程中，团队成员间需要激烈讨论，这种团队讨论一方面可以培养成员的语言表达能力、沟通协调能力和团结推进能力，另一方面是一个不断反省、不断尝试、探索创新及提升实际应用能力的一个过程。数学建模竞赛平台吸引了越来越多的经管类专业学生参与，据统计参加建模竞赛和获得奖项的同学中经管类学生超过了6%[2]，在这种合作活动中学生的团结协作能力得到了显著的提升。

5 结束语

以建模为驱动的经管类专业图论教学模式能够为学生增强学习兴趣，提高学习效率提供有力支撑，对培养学生创新能力和沟通协调能力提供有效的平台。教学方法和模式的改变需要在实际教学中不断总结，逐渐实现图论教学效果的提升。

[1]孙惠泉.图论及其应用[M].北京:科学出版社，2004.

[2]姜启源，谢金星.一项成功的高等教育改革实践——数学建模教学与竞赛活动的探索与实践[J].中国高教研究，2011(12):79-83.

[3]冯芷艳，郭迅华，曾大军，等.大数据背景下商务管理研究若干前沿课题[J].管理科学学报，2013，16(1):1-9.

[4]王志刚，姚云飞.“最值定理”的教学探究[J].阜阳师范学院学报:自然科学版，2014，31(1):79-81.

[5]Euler L. Solutio problematis ad geometriam situs pertinentis[J]. Commentarii Academiae Scientiarum Petropolitanae(8): 128-140.

[6]Codenotti B，Manzini G，Margara L，et al. Perturbation:an efficient technique for the solution of very large instances of the euclidean TSP[J]. INFORMS Journal on Computing，1996，8(2): 125-133.

[7]Angel E，Bampis E，Gourvès L. Approximating the pareto curve with local search for the bicriteria TSP(1，2)problem[J]. Theoretical Computer Science，2004，310(1/3): 135-146.

[8]Appel K，Haken W. The four color theorem[J]. Scientific American，1977，236(4): 108-121.

[9]程 钊. 图论中若干著名问题的历史注记[J]. 数学的实践与认识，2009，39(24):73-81.

[10]Lazer D，Pentland A S，Adamic L，et al. Life in the network:the coming age of computational social science[J]. Science，2009，323(5915): 721.

[11]Zhu Zhiguo. Discovering the influential users oriented to viral marketing based on online social networks[J].Physica a: Statistical Mechanics and Its Applications，2013，392(16): 3459-3469.

[12]赵 静，但 琦. 数学建模与数学实验[M]. 北京＆nbsp;＆nbsp;海德堡:高等教育出版社，施普林格出版社，2000.

[13]Doan A，Ramakrishnan R，Halevy A Y. Crowdsourcing systems on the World-Wide web[J]. Communications of the ACM，2011，54(4): 86-96.