基于Mathematica软件在常微分方程初值问题中的可视化

孔祥强

(菏泽学院数学系，山东菏泽 274015)



基于Mathematica软件在常微分方程初值问题中的可视化

孔祥强

(菏泽学院数学系，山东菏泽 274015)

基于Mathematica软件的功能特点，针对常微分方程数值解的3种常见算法，本文通过编程实现了在同一界面下、不同算法之间的动态可视化操作，直观地验证了3种方法的优劣，并通过具体的数值算例验证了操作的可行性。

Mathematica软件；可视化；数值解；初值问题；常微分方程

Mathematica是一款有关科学计算的软件，它将符号计算、图形描绘和数值计算有效地结合起来.该软件有如下特点：(1)简单易学，操作方便；(2)强大的绘图和动态显示功能；(3)编程语言精练，效率高；(4)与其它数学软件可互相调用[1].Mathematica软件广泛应用于图形绘制、动态模拟、随机模拟和物理现象模拟等诸多方面[2].常微分方程是一门较抽象的学科，其中的一些算法不好理解，比如求微分方程数值解的几种算法，利用Mathematica软件可使这些复杂的问题简单化、直观化.通过Mathematica软件，可实现方程数值解的可视化操作，使多种不同的计算方法在同一界面下显示出来；通过参数的调整，由图像直观观察出数值解与解析解的误差，从而对算法的优劣进行判定，达到抽象内容具体化、教学内容直观化和提高教学质量的目的.

1 常微分方程初值问题的3种常用解法

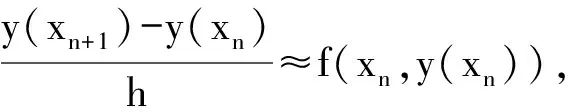
一般地有yn+1=yn+hf(xn,yn),n=0,1,2,…，N-1.

称该式为Euler法公式.Euler法的局部截断误差的阶为O(h2)，为一阶精度的方法[4].Euler法有明显的几何意义.以f(x0,y0)为斜率，过点(x0,y0)做直线，它与直线x=x1的交点为y1，依次类推，yn+1是以f(xn,yn)为斜率，过点(xn,yn)的直线与直线x=xn+1的交点，故Euler法也称为折线法[5].

称上式为梯形法公式，梯形法为二阶精度的方法[3].

Runge-Kutta法是一种非线性的高阶单步法，该方法的导出基于Taylor展开，故要求所求的解有较高的光滑度，对于光滑性不太好的解，最好采用低阶算法而将步长取小.经典的四阶Runge-Kutta法的计算公式为

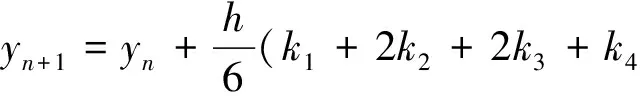
其局部截断误差为O(h5)，为四阶精度的方法，阶数越高，方法越精确[5].

2 3种算法的动态可视化实现

Euler法、梯形法和Runge-Kutta法均可求方程的数值解，下面通过数值算例动态演示算法的解题过程，从中了解3种算法的优劣.

若用3种方法单独求每一个方程的初值问题比较繁琐，计算量大，且不易比较3种方法的优缺点.下面通过Mathematica软件编程，可动态观察3种算法的计算过程，从而实现以下功能：(1)通过下拉菜单选择不同的方程,再进一步动态选择Euler法、梯形法或Runge-Kutta法；(2)作出微分方程解析解的图像及数值解的折线图；(3)对每一个方程，可以选择不同的步长h(不妨设0.1≤h≤2)，且能在图像上反映出节点个数，并显示出h的具体值；(4)通过同一窗口下直观比较数值解和解析解的误差，对3种方法进行比较；(5)通过微调x轴、y轴，选择不同的视角观察图形.

实现以上功能的源程序：

f1[x_,y_]:=y-2.01x;f2[x_,y_]:=-1.01y^2;

f3[x_,y_]:=-1.01x^2y;f4[x_,y_]:=x^2-2.01y;

f5[x_,y_]:=Sin[1.01x]y;f6[x_,y_]:=(x-x^2)y;

p[x_,y_]:={x,y};

q[x_List,y_List]:=MapThread[p,{x,y}];

jie[a_,s_,y0_,t_]:=DSolve[{y’[t]s[t,y[t]],y[a]y0},y,t];

dian={ImageSize450,PlotRangePadding0.41};

s1[{a_,b_},s_,y0_,n_]:=Module[{h,x,y,u},h=(b-a)/n;

x=Table[a+(j-1)h,{j,1,n+1}];

y=Table[0,{n+1}];y[[1]]=y0;

Do[y[[j]]=y[[j-1]]+hs[x[[j-1]],y[[j-1]]],{j,2,n+1}];u=q[x,y]];

t1[{y0_,x0_,h_,s_},{D_,b_,d_}]:=Module[{g,z},g=Length[b];

z=Table[0,{j,1,g}];z[[1]]=s[x0,y0];

Do[z[[j]]=s[x0+d[[j]]h,y0+hSum[D[[j-1,k]]z[[k]],{k,1,j-1}]],{j,2,g}];

yn=y0+hSum[b[[j]]z[[j]],{j,1,g}]];

t2[{a_,r_},s_,y0_,n_,{D_,b_,d_}]:=Module[{h,x,y,v,j},h=(r-a)/n;

x=Table[a+(j-1)h,{j,1,n+1}];

y=Table[0,{n+1}];y[[1]]=y0;

Do[y[[j]]=t1[{y[[j-1]],x[[j-1]],h,s},{D,b,d}],{j,2,n+1}];

v=q[x,y]];

s2[{a_,r_},s_,y0_,n_]:=Module[{D,b,d},D={{1/2}};

b={0,1};d={0,1/2};

t2[{a,r},s,y0,n,{D,b,d}]];

s3[{a_,r_},s_,y0_,n_]:=Module[{D,b,d},D={{1/2},{0,1/2},{0,0,1}};

b={1/6,1/3,1/3,1/6};d={0,1/2,1/2,1};t2[{a,r},s,y0,n,{D,b,d}]];

Manipulate[Show[{Plot[Evaluate[y[t]/.jie[a,s,d,t]],{t,a,b+0.1},

PlotStyle{Orange,Thick},AxesOrigin{0,0},PlotRangeAll,

PlotLabelRow[{

Style["步长:",16,Bold,Red],Style[N[(b-a)/qq,12],16,Brown]}]],

ListPlot[Tooltip[Check[fangfa[{a,b},s,d,If[MemberQ[{f3,f5,f6},s],N[qq],qq]],{a}]],PlotStyle{Blue,PointSize[0.016]}],

ListLinePlot[Check[fangfa[{a,b},s,d,If[MemberQ[{f3,f5,f6},s],

N[qq],qq]],{a,d}],PlotStyle{Blue,Dashed},PlotRangeAll]},

ImageSize600,AxesStyleArrowheads[0.02],

Epilog

{Text[Framed[Column[{Row[{Style["-",Red,Bold,18],

Style["方程的解析解",14,Bold,Magenta]}],

Row[{Style["-",Blue,Bold,18],Style["方程的数值解",14,Bold,Magenta]}]}]],{1,0.8},{1,0.8}]}],{{s,f1,

Style["选择方程y'=",13,Blue,Bold]},{f1"y-2.01x",

f2"-1.01y2",f3"-1.01x2y",f4"x2-2.01y",

f5"Sin[1.01x]y",f6"(x-x2)y"},

ControlTypePopupMenu,ControlPlacementBottom},

{{fangfa,s1,Style["选择方法",13,Brown,Bold]},{s1"Euler法",

s2 "梯形法",s3 "Runge-Kutta法"},ControlPlacementBottom},

Delimiter,{{qq,5,

Style["选择步长",13,Blue,Bold]},1,20,1,ControlPlacementBottom,

Appearance"Labeled"},Delimiter,{{a,0,

Style["向左微调x轴",13,Bold,Green]},-1/3,1/3,1/5,

Appearance"Labeled",ControlPlacementBottom},{{b,2,

Style["向右微调x轴",13,Bold,Green]},1,3.5,1/4,

ControlPlacementBottom,Appearance"Labeled"},

{{d,1,Style["上下微调y轴",13,Bold,Green]},1/2,5/2,1/5,

ControlPlacementBottom,Appearance"Labeled"},

TrackedSymbolsManipulate,SaveDefinitionsTrue]

输出结果：

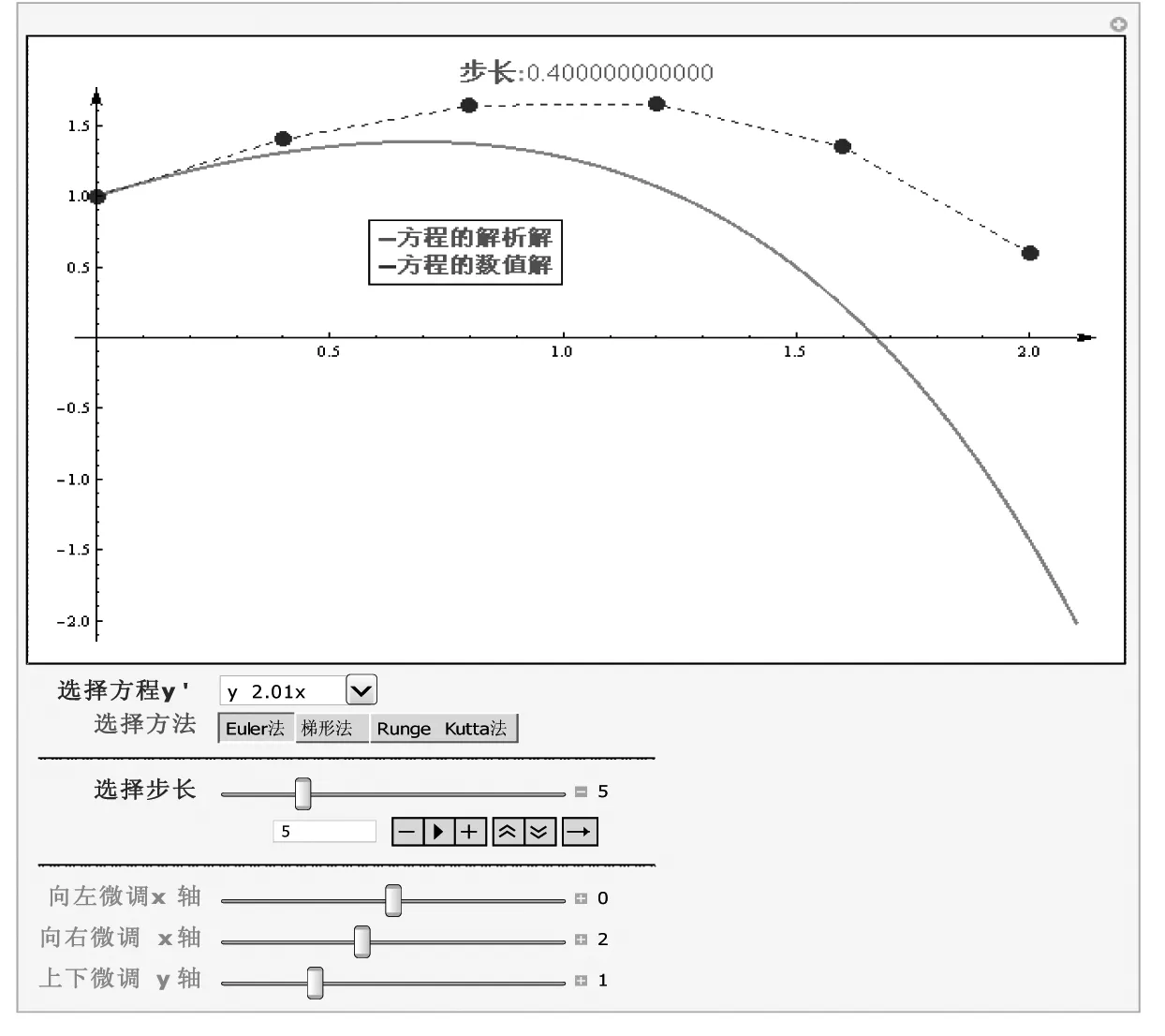
图1 用Euler法求初值问题y′=y-2.01x,y(0)=1

图1中，连续曲线为方程解析解的图形，折线为数值解图像；步长为0.400000000000，通过单击“动画控件”按钮，可实现步长的自动播放功能.通过窗口最下方的3个微调按钮，可选择合适的视角观察图形.

图2 用梯形法求初值问题，y′=y-2.01x,y(0)=1

图2选择的是梯形法，与图1比较，在同步长的情形下，梯形法所得数值解产生的误差明显小于Euler法，梯形法是比Euler法更精确的方法.在调节步长的同时，节点也随时变化.随着步长的减小，图形的节点动态增加.节点个数越多，所得数值解折线和解析解曲线越吻合.

图3采用Runge-Kutta法解同一个初值问题，与图1和图2比较可知，该法所得数值解曲线和解析解曲线基本一致，是3种方法里误差最小的，是比Euler法和梯形法都要精确的方法.

图4 用Euler法求初值问题y′=x2-2.01y,y(0)=1

图4中选择的方程为y′=x2-2.01y，通过下拉菜单也可以选择y′=-1.01y2或y′=-1.01x2y或y′=sin(1.01x)·y或y′=(x-x2)y，这样求解速度快，大大提高了做题效率，实用性强.案例中的微分方程，完全可以更换为其它方程，只需将源程序中的函数表达式改为其它表达式即可，因此程序具有一般性.

3 结语

通过案例可看出，利用Mathematica软件编程，可达到将复杂问题简单化、直观化的目的[6].在教学中，能够突破教学难点，激发学生的学习兴趣，使他们更好地理解和认识所学的各种算法，以达到提高解决实际问题能力的目的.Mathematica软件的使用为数学教学注入了生命力，使数学软件和数学教学有机地结合起来，成为一种新型的教学方法和手段.

[1]王绍恒,王艺静.Mathematica软件在大学数学课程教学中的应用[J].教育理论与实践,2013,33(21):39-40.

[2]李士恒.Mathematica在数学实验中的应用[J].中央民族大学学报:自然科学版,2014,23(3):14-17.

[3]关治,陈景良.数值计算方法[M].北京:清华大学出版社,2005:236-242.

[4]李荣华,刘播.微分方程数值解法[M].北京:高等教育出版社,2011:1-37.

[5]张韵华,奚梅成,陈效群编.数值计算方法与算法[M].北京:科学出版社,2006:168-186.

[6]程春蕊,朱军辉.Mathematica软件在常微分方程教学中的应用[J].高等函授学报:自然科学版,2012,25(1):21-23.

Mathematica-based Visual Insight in the Initial Value Problems of Ordinary Differential Equation

KONG Xiang-qiang

(Department of Mathematics of Heze University, Heze Shandong 274015, China)

Based on the functions and characteristics of the Mathematica software, in view of the numerical solution of three common algorithms of ordinary differential equations,we realized the dynamic visualization operation under the same interface between different algorithms through the programming. The advantages and disadvantages of three kinds of method were verified, and we verified the feasibility of operation by detailed numerical examples.

Mathematica software; visualization; numerical solution; initial value problems;ordinary differential equation

2015-07-17

菏泽学院重点课题组项目(201311)。

孔祥强(1983- )，男，山东菏泽人，菏泽学院数学系讲师，硕士，从事计算数学研究。

O245

A

2095-7602(2015)10-0020-06