区间直觉模糊数的精确函数及其在决策中的应用
康 婧, 兰 蓉, 王莎莎
(1.西安邮电大学 通信与信息工程学院, 陕西 西安 710121; 2.西北大学 信息科学与技术学院, 陕西 西安 710127)
区间直觉模糊数的精确函数及其在决策中的应用
康 婧1, 兰 蓉1, 王莎莎2
(1.西安邮电大学 通信与信息工程学院, 陕西 西安 710121; 2.西北大学 信息科学与技术学院, 陕西 西安 710127)
针对区间直觉模糊数的排序问题,定义一种新的区间直觉模糊数精确函数。在考虑犹豫度信息的情况下,讨论了该精确函数的性质。通过实例与已有的精确函数比较,结果显示,该精确函数的排序能力有一定程度的提高。最后将其应用到区间直觉模糊多属性决策中,并用实例分析验证该方法的有效性。
区间直觉模糊数;犹豫度;精确函数;多属性决策
模糊集及其相关理论[1]为解决涉及不精确性、不确定性信息的问题提供了一种有力的工具。直觉模糊集[2]相对传统的模糊集理论,在解决模糊性和不确定性等问题时具有更好的灵活性和实用性,这是因为直觉模糊集同时考虑了隶属度、非隶属度以及犹豫度3方面的信息,使得它在对事物属性的刻画上更全面,表现能力更强[3]。随着直觉模糊集概念的推广,区间直觉模糊集的概念被引入,将隶属度、非隶属度和犹豫度分别用[0,1]上的区间数表示,并定义了区间直觉模糊集的基本运算法则[4]。
区间直觉模糊集理论被广泛应用于诸多领域,尤其是多属性决策分析[5-7]方面。在这种基于区间直觉模糊集的多属性决策过程中,对区间直觉模糊数的排序是不可或缺的一个环节,因此有关区间直觉模糊数排序的问题日益凸显出其重要性,并引起了广泛关注。针对区间直觉模糊数的排序问题文献[8]提出了得分函数和精确函数来实现区间直觉模糊数的排序,随后文献[9]提出一种新的精确函数用来排序,文献[10]在文献[8]和文献[9]的基础上得到一种改进的精确函数。然而,在某些情况下使用这些已有的得分函数和精确函数仍然无法比较区间直觉模糊数的优劣,即存在排序失效的情况。
本文研究区间直觉模糊数的排序问题,在考虑犹豫度的情况下定义一种新的区间直觉模糊数的精确函数,借助新的精确函数提出一种区间直觉模糊数的排序算法,并通过若干区间直觉模糊数的排序结果验证该算法的有效性。将此排序算法应用于区间直觉模糊多属性决策问题,并通过相关实例验证该方法的有效性。
1 预备知识
1.1 直觉模糊集和区间直觉模糊集
直觉模糊集是模糊集概念的延伸。
定义1[2]设X是个非空集合,则定义
A={(x,μA(x),νA(x)):x∈X}
为直觉模糊集。其中映射
μA(x):X→[0,1]
是元素x属于直觉模糊集A的隶属度,而映射
νA(x):X→[0,1]
则是非隶属度,并且满足
0≤μA(x)+νA(x)≤1 (x∈X)。
但实际上,很难用精确的数值来刻画元素对概念的隶属度和非隶属度,因此,在这种情况下更适合用区间数来表示。于是区间直觉模糊集的概念被提出。
定义2[3]设D[0,1]是区间[0,1]上的所有闭子集的集合,则定义
是X上的区间直觉模糊集,其中
满足条件
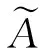

其中
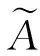
1.2 区间直觉模糊集的相关运算



其中
[a,b]∈D[0,1],[c,d]∈D[0,1],b+d≤1。
则可为区间直觉模糊数定义运算法则如下。
定义4[8]其中
(1) 补运算
(2) 和运算
(3) 乘运算
(4) 数乘运算
(5) 指数运算
1.3 区间直觉模糊集成算子
使用区间直觉模糊加权算数平均算子,定义如下。
定义5[8]设Ai(i=1,2,…,m)为区间直觉模糊数,则定义加权算术平均算子为
其中

1.4 区间直觉模糊集的得分函数和精确函数
在基于区间直觉模糊数的多属性决策方法中,区间直觉模糊数的排序一直是个很关键的问题,因此定义得分函数和精确函数。
定义6[8]设A=([a,b],[c,d])是区间直觉模糊数,则分别称
为A的得分函数和精确函数,其中
S(A)∈[-1,1], H(A)∈[0,1]。
得分函数S与精确函数H比较类似于统计学中的均值和方差。因此基于S(A)与H(A)两个指标,文献[8]提出了如下排序方法。
若A1=([a1,b1],[c1,d1])和A2=([a2,b2],[c2,d2])为任意两个区间直觉模糊数,则
(1) 若S(A1)>S(A2),则A1>A2;
(2) 若S(A1)=S(A2),则当
H(A1)=H(A2)时,A1=A2;
H(A1)>H(A2)时,A1>A2。
此方法只考虑了隶属度与非隶属度区间,并未将犹豫度区间信息考虑在内,所以在对一些区间直觉模糊数排序时依然会存在失效的情况。文献[9]在考虑了犹豫度区间π=[1-b-d,1-a-c]的情况下提出了新的精确函数。
定义7[9]设A=([a,b],[c,d])是区间直觉模糊数,则称
为A基于犹豫度的精确函数。M(A)∈[-1,1]。
随后文献[10]在文献[8]和文献[9]的基础上进一步改进了区间直觉模糊数的精确函数,得到了一种改进后的精确函数。
定义8[10]设A=([a,b],[c,d])是区间直觉模糊数,定义
为A基于犹豫度的精确函数。L(A)∈[-1,1]。
但这些得分函数和精确函数在对一些区间直觉模糊数排序时仍存在失效的情况,以下举例说明。
例1 对区间直觉模糊数
A1=([0.5,0.6],[0.1,0.3]),A2=([0.6,0.7],[0.05,0.15])
排序。
用定义6可得
H(A1)=0.75, H(A2)=0.75。
在这种情况下,文献[8]提出的精确函数不能有效的对这两个区间直觉模糊数排序,故失效。
例2 对区间直觉模糊数
A1=([0.3,0.5],[0.3,0.4]),A2=([0.3,0.5],[0.2,0.3])
排序。
用定义6可得
H(A1) =0.75, H(A2)=0.65,
用定义7得
M(A1)=0.15, M(A2)=0.05,
但A1⊂A2,由于两个区间直觉模糊数的隶属度相同,而A1的非隶属度大于A2,考虑到实际情况A2应该优于A1,而定义6和定义7中的精确函数给出的排序却是A1>A2,故定义6及定义7对此区间直觉模糊数的排序与实际情况不符。
例3 对区间直觉模糊数
A1=([0,0.4],[0,0.6]),A2=([0.2,0.4],[0.4,0.4])
排序。
用定义8得
L(A1)=0.02, L(A2)=0.02。
在此情况下定义7中的精确函数不能对其做出正确排序,故失效。
例4 对区间直觉模糊数
A1=([0.45,0.65],[0.15,0.25]),A2=([0.5,0.6],[0.1,0.3])
排序。
用定义6可得
H(A1)=0.75, H(A2)=0.75,
用定义7得
M(A1)=0.3, M(A2)=0.3,
用定义8得
L(A1)=0.465, L(A2)=0.465。
即上述3种排序法均不能对此区间直觉模糊数进行正确排序,故在此排序中均失效。
2 新的精确函数
对于区间直觉模糊数来说,隶属度越大越好,非隶属度越小越好,此外犹豫度也是越小越好。以一项满意度问卷调查模型为例,隶属度越大表示越满意,非隶属度越大则表明越不满意,而犹豫度则表示未完成的问卷,若将未完成的问卷再次让当事人做完,又能得到部分满意或不满意的答案,于是考虑将犹豫度信息根据实际情况转化成部分非隶属度信息来给出一种新的精确函数,具体定义如下。
定义9 设A=(μA(x),νA(x))是区间直觉模糊数,其中
μA(x)=[a,b]⊂[0,1],νA(x)=[c,d]⊂[0,1]
分别表示其隶属度区间和非隶属度区间,且
0≤b+d≤1,
于是犹豫度区间可表示为
πA(x)=1-μA(x)-νA(x)=[1-b-d,1-a-c],
则定义其精确度函数为
基于精确函数S′(A),定义如下区间直觉模糊数的一种排序方法。
定义10 若A1=([a1,b1],[c1,d1])和A2=([a2,b2],[c2,d2])为任意两个区间直觉模糊数,S′(A1)>S′(A2),则A1>A2。
精确度函数S′满足如下性质。
定理1 设A=([a,b],[c,d])是一个区间直觉模糊数,S′(A)是其精确度函数,则有
(1) -1≤S′(A)≤1;
(2) S′(A)=1时,A取最大值([1,1],[0,0]);
(3) S′(A)=-1时,A取最小值([0,0],[1,1])。
定理2 设A1=([a1,b1],[c1,d1])和A2=([a2,b2],[c2,d2])为任意两个区间直觉模糊数,若A1⊆A2,则S′(A1)≤S′(A2)。
证明 区间直觉模糊数的精确度函数表示为
其中a,b,c,d∈[0,1],且
a≤b, c≤d, b+d≤1。
于是对于S′(A)求关于a的偏导数,则
即S′(A)关于a是单调递增的。
对S′(A)求关于b的偏导数,则
即S′(A)关于b也是单调递增的。
接着对S′(A)求关于c的偏导数,则
则意味着S′(A)关于c是单调递减的。
再对S′(A)求关于d的偏导数,则
则意味着S′(A)关于d是单调递减的。
由于A1⊆A2,则对两个区间直觉模糊数有
a1≤a2, b1≤b2, c1≥c2, d1≥d2;
再结合S′(A)分别关于a,b,c,d的单调性可得
S′(A1)≤S′(A2)。
证毕。
定义10的排序方法考虑了区间直觉模糊数犹豫度对排序的影响,能使区间直觉模糊数排序更精确。使用定义9的精确函数给上述例子中的区间直觉模糊数排序。
将定义10应用于上述例1,得到
S′(A1)=0.285, S′(A2)=0.52,
故A1 将定义10应用于上述例2,得到 S′(A1)=-0.045, S′(A2)=0.055, 故A1 将定义10应用于上述例3,得到 S′(A1)=-0.4, S′(A2)=-0.22, 故A1 将定义10应用于上述例4,得到 S′(A1)=0.2925, S′(A2)=0.285, 故A1>A2。 所以本文提出的排序法能对上述几组区间直觉模糊数排序失效的情况做出正确的比较,对区间直觉模糊数比较的覆盖范围更广,具有较好的分辨性和较强的推广性。 针对区间直觉模糊多属性群决策问题进行讨论,并采用上述定义的新的精确函数给出具体的决策方法。区间直觉模糊多属性决策问题的具体模型如下。 其中 方便起见,分别记 运用精确函数区间直觉模糊数排序的方法,给出一种基于WAA(加权算数平均)算子下区间直觉模糊多属性决策方法,具体步骤如下。 (3) 基于定义10对候选方案Ai(i=1,2,…,m)进行排序并得到最佳方案。 某学校在对奖学金获得者进行评选时,制定了5项考查指标(属性):C1为考试成绩、C2为思想品德、C3为参加竞赛获奖情况、C4为论文发表情况、C5为班级贡献。各项指标的权重向量为 ω=(0.2, 0.1, 0.3, 0.3, 0.1)T。 通过自我申请、导师推荐、评议,对各候选人按照以上5项指标进行评定,统计处理后确定了4位候选人Ai(i=1,2,3,4)。若每位候选人的5项指标评定信息经过统计处理,可以表示为区间模糊数,则各方案对应的属性值如表1所示。 表1 各方案的属性值 以下用本文中的方法排序并选择最佳候选人。 A2>A4>A1>A3, 所以最佳候选人为A2。 为了在决策过程中,更有效、合理地对区间直觉模糊数进行排序,提出了一种新的精确函数,该精确函数在考虑了隶属度和非隶属度的同时还将部分犹豫度信息也考虑其中,从而改善区间直觉模糊数的排序性能,并达到更好的排序效果,最后给出了基于该精确函数的一种决策方法,并用实验数据证明了该算法的可行性及有效性。 [1] Zadeh L.Fuzzy Sets[J].Information and Control,1965,8(3):338-353. [2] Atanassov K.Intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems,1986,20(1):87-96. [3] 兰蓉. 基于直觉模糊集相似度量的多属性决策方法[J].西安邮电学院学报,2010,15(3):64-67. [4] Atanassov K,Gargov G.Interval valued intuitionistic fuzzy sets[J].Fuzzy Sets and Systems,1989,31(3):343-349. [5] 张英俊,马培军,苏小红.属性权重不确定条件下的区间直觉模糊多属性决策[J].自动化学报,2012,38(2):220-228. [6] 兰蓉,范九伦.一种基于三角模糊数的理想点多属性决策方法[J].西安邮电学院学报,2009,14(5):164-168. [7] 徐泽水.不确定多属性决策方法及应用[M].北京:清华大学出版社,2005:116-155. [8] 徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用[J].控制与决策,2007,22(2):215-219. [9] Ye Jun.Multicriteria fuzzy decision-making method based on a novel accuracy function under interval-valued intuitionistic fuzzy enviroment[J].Expert Systems with Applications,2009,(36):6899-6902. [10] Lakahmana V,Muralikrishnan S,Sivaraman G.Multi-criteria decision making method based on interval-valued intuitionistic fuzzy sets[J].Expert Systems with Applications,2011,38(3):1464-1467. [11] 王中兴,牛利利.区间直觉模糊数的新得分函数及其在多属性决策中的应用[J].模糊系统与数学,2013,27(4):167-172. [责任编辑:祝剑] A new accuracy function of interval-valued intuitionistic fuzzy numbers and its application in decision making KANG Jing1, LAN Rong1, WANG Shasha2 (1. School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications,Xi’an 710121,China;2. School of information and technology, NorthWest University, Xi’an 710127, China) A new way to define a new accuracy function of interval-valued intuitionistic fuzzy numbers is proposed for sorting the interval-valued intuitionistic fuzzy numbers in this paper. The properties of the function are discussed based on considering the information of hesitancy degree. Some examples are designed and compared with some existing accuracy functions. The results show that the sorting capability of the new accuracy function is improved to the certain extent. At last, this new accuracy function is applied to the multiple attribute decision making on interval-valued intuitionistic fuzzy numbers and its effectiveness is illustrated by a numerical example. interval-valued intuitionistic fuzzy numbers, hesitancy degree, accuracy function, multiple attribute decision making 2015-01-23 康婧(1990-),女,硕士研究生,研究方向为信息处理技术与应用。E-mail: 348203128@qq.com 兰蓉(1977-),女,博士,副教授,从事决策分析和模式识别研究。E-mail: ronglanlogic@163.com 10.13682/j.issn.2095-6533.2015.03.015 TP18;O235;C934 A 2095-6533(2015)03-0086-063 基于新的精确函数的模糊多属性决策

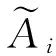
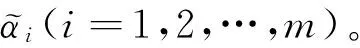
4 实例分析


5 结束语

