First Principles Molecular Dynamics Computation on Ionic Transport Properties in Molten Salt Materials

Chung-Fu Chen,Yi-Chia Cheng and Che-Wun Hong,2

First Principles Molecular Dynamics Computation on Ionic Transport Properties in Molten Salt Materials

Chung-Fu Chen1,Yi-Chia Cheng1and Che-Wun Hong1,2

Based on the Hellmann-Feynman theorem,which integrates the molecular dynamics simulation with computational quantum mechanics,this research simulates the ionic transport in the LiCl-KCl molten salt materials using so called “first principles molecular dynamics(FPMD)”technique without employing an empirical potential model.The main purpose of this computational FPMD focuses on the evaluation of important transport properties,such as diffusion coefficient,ionic conductivity,shear viscosity,and thermal conductivity,using the Green-Kubo relationship.All simulation results agree well with experimental data published in existing literatures within an acceptable range.FPMD calculations are proved to be a powerful tool for prediction of the molecular structure,transport properties,as well as ionic interactions from the microscopic aspect.It is expected to integrate further with a multi-scale simulation tool for future function expansion to macroscopic performance prediction.

first principles molecular dynamics(FPMD),molten salt,diffusion coefficient,ionic conductivity,shear viscosity,thermal conductivity.

1 Introduction

Due to the superior stability of molten salts at both high and low temperatures,there are many engineering applications,such as stationary energy storage[Bradwell,Kim,Sirk,and Sadoway(2012)],pyro-chemical treatment of nuclear wastes[Fukasawa,Uehara,Nagai,Sato,Fujii,and Yamana(2012)],as a coolant in nuclear reaction processes[Waldrop(2012);Brun(2007)],and being electrolytes in thermally activated batteries[Guidotti and Masset(2006);Masset and Guidotti(2007);Masset,Henry,Poinso,and Poignet(2006)].Additionally,similar phase change materials can be applied to modern micro and nano technologies,such asa micro heatsinkfor the cooling of electronic components[Faraji,Mustapha,and Mostafa,(2014)],thermal doping on semiconductors[Eslamian and Saghir(2012)],and rapid accumulation of particles suspended in a thermocapillary liquid bridge[Kuhlmann,Lappa,Melnikov,Mukin,Muldoon,Pushkin,Shevtsova,and Ueno(2014)].E-specially under high temperature operating conditions,molten salt batteries can provide extremely high output power due to the high ionic conductivity achieved in molten electrolytes.They can sustain high level of mechanical and thermal stress[Masset(2006);Masset,Schoeffert,Poinso,and Poignet(2005)]with superior stability in long-time storage[Haimovich,Dekel,and Brandon(2009);Haimovich,Dekel,and Brandon(2015);Fujiwara,Inaba,and Tasaka(2011)].Due to extensive utilizations in various applications,their transport properties(diffusion coefficient,ionic onductivity,shear viscosity,and thermal conductivity etc.)become the main concern in macroscopic performance evaluations.However,measurements on high temperature molten salts can be costly and limited,computational simulation techniques provide a powerful tool for evaluating the transport properties,as well as details in molecular structures and ionic interactions,provided that a proper mathematical model can be set up[Srivastava and Atluri(2002)].

To date,classical molecular dynamics(MD)potential models contain the physics of ionic attraction,repulsion,dispersion and polarization effects etc.,they can be used to predict many properties of molten salts and their solutes[Frenkel and Smit(1996);Lantelme and Turq(1982);Caccamo and Dixon(1980);Cheng Lee,and Hong(2007);Cheng,Chen,and Hong(2008);Chen,Li,and Hong(2015)].Fumi and Tosi(1964)developed potential functions and then tuned all parameters for all kinds of alkali halides to reproduce the properties of crystals.Galamba,Castro,and Ely(2004,2005,2007)successfully computed the shear viscosity and thermal conductivity of molten KCl and NaCl with equilibrium MD and non-equilibrium MD simulations.Nevins and Spera(2007)examined the various calculation conditions to obtain a good compromise between simulation time and viscosity output quality.Although many research reports have depicted those on typical molten alkali halides using MD simulations,it is still a troublesome matter to fit many semi-empirical potential parameters that could be time-consuming and subject to inevitable uncertainties.

First principles molecular dynamics(FPMD)simulations are a new technique to deal with the potential functions between various atoms and ions,but still keep the methodology of the classical MD.They can be computationally intensive and therefore are limited to much smaller systems and shorter simulation time than classical MD methods[Galamba and Cabral(2007a,2007b);San,Chiu,and Hong(2011);San and Hong(2011);Bengston,Nam,Saha,Sakidja,and Morgan(2014)].The main purpose of the FPMD simulation in this paper focuses on the evaluation of important transport properties,such as diffusion coefficient,ionic conductivity,shear viscosity,and thermal conductivity of molten LiCl-KCl systems.All simulation results will be compared against experimental data or classical MD results(if no experimental results available)published in existing literatures.

2 Methodology

The FPMD simulation technique in this paper is based on the Hellmann-Feynman(H-F)theorem which integrates the MD simulation with computational quantum mechanics[Hong and Tsai(2010)].H-F theorem mainly describes how to calculate the total energy and its spatial gradient in the Hamiltonian system;that can be expressed by:

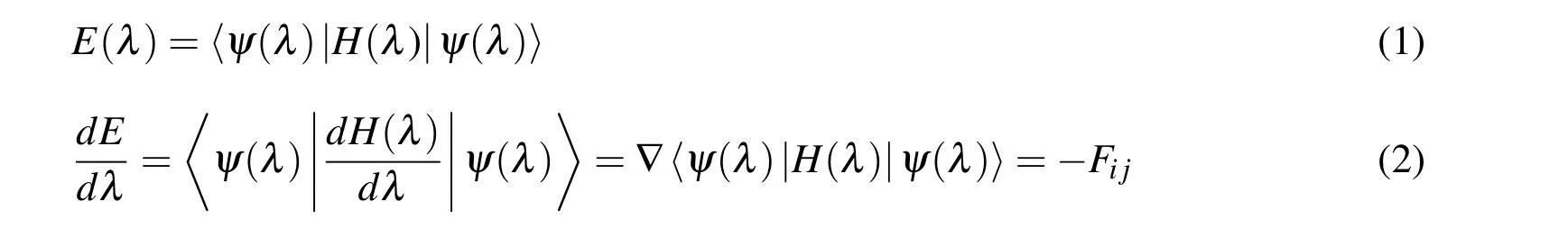
where E is the total energy,ψ is the wave function,H is the Hamiltonian operator,λ is a specified nuclear position,and Fijis the inter-molecular force between atoms i and j.If λ is a given degree of freedom of the system,then the term dE/dλ given by Eq.(2)can be interpreted as the generalized inter-molecular force.The methodology of the FPMD simulation in this paper is to employ the density functional theory(DFT),which calculates the density functional instead of the wave function of a multi-electron system[Kohn and Sham(1965);Hong and Chen(2011)].For a system of n electrons,ρ(r)represents the total electron density at a particular position r in space.The electronic energy,denoted by E[ρ],is considered as a functional of the electron density.There is a single corresponding electronic energy E[ρ]for a given function ρ(r).The precise electron density and the electronic energy in the DFT are expressed by:

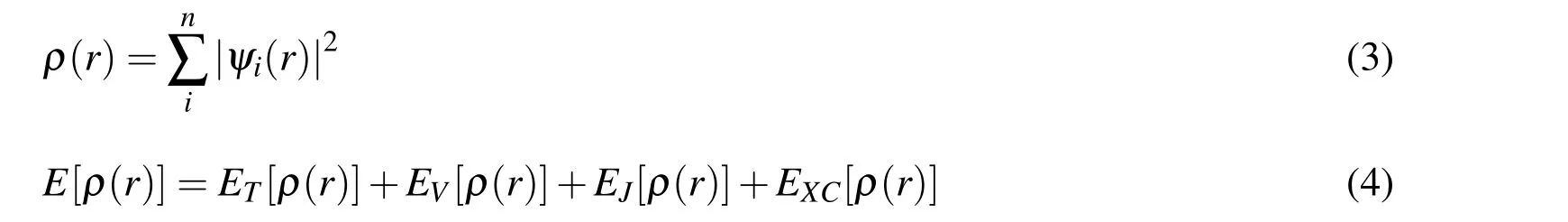
where ETis the kinetic energy term arisen from the motion of the electrons;EVincludes the potential energy of the nuclear-electron attraction and the repulsion between pairs of nuclei;EJis the electron-electron repulsion term;and EXCrepresents the exchange-correlation term which includes the remaining part of the electronelectron interactions.All terms are functions of electron density function ρ(r),except for the nuclear-nuclear repulsion.Our FPMD simulations were carried out on the CASTEP(Cambridge serial total energy package)platform[Segall Lindan,Probert,Pickard,Hasnip,Clark,and Payne(2002);Clark,Segall,Pickard,Hasnip,Probert,Refson,and Payne,(2005)].The first step was to optimize the molecular structures of LiCl,KCl,and eutectic LiCl-KCl electrolytes by minimizing the total energy of the simulation system.All simulations were run with the canonical ensemble(NPT)using the Nosé-Hoover thermostat[Nosé(1984)]for 200 time steps on LiCl and KCl,and 400 time steps on eutectic LiCl-KCl to equilibrate the simulation system.Energy cutoff was set at 300 eV and periodic boundary conditions(PBCs)were employed in both classical MD and FPMD to represent a macro-size bulk material.

3 Results and Discussions

3.1 Convergence tests

Since FPMD simulations are computationally intensive,normally we try the best to reduce the simulation time by decreasing the number of atoms involved.However,that will incur numerically unstable and divergence as well as inaccuracy.Convergence tests were carried out to check if the number of atoms in a single unit cell with 16,32,64,128,256,512,and 1024 atoms is enough during a reasonable simulation time(8 ps).Figure 1 shows that the simulation results of the system density,total energy,and diffusion coefficient tend to converge when the number of atoms is above 256 atoms per unit cell.The error bars in the diagram show that the fluctuation ranges from 7%to 10%if we choose 16 to 128 atoms.If the atom number is greater than 256,all error bars become much shorter(less than 3%).Hence,in the later cases of this paper we will set the number at 256 atoms per unit cell.

Figure 2 shows that we tried to test how long the FPMD simulation should perform.The simulation time was set from 2 to 48 ps(time step is 2fs in each case)and the results found that after 16 ps,all error bars became very small and the results could be converged.Table 1 specially compares the predicted density of the system with those experimental data from Janz,Allen,Bansal,Murphy,and Tomkins(1979).All simulation and experimental results of molten LiCl,KCl,and eutectic LiCl-KCl salts are in good agreement.

3.2 Molecular structure analysis

To investigate if the molecular structure of high temperature molten salts at pseudoliquid(molten)state or not,the radial distribution function(RDF)for the system has to be examined.RDF,denoted as g(r),is a spatial parameter to investigate the molecular structure by counting the local number density divided by the system density.The mathematical definition of g(r)is expressed by

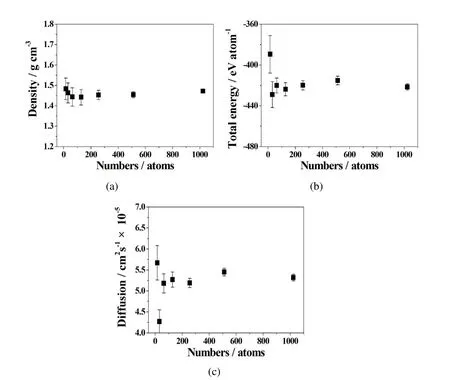
Figure 1:Convergence tests of(a)density,(b)total energy,and(c)diffusion coefficients,with different number of 16,32,64,128,256,512,and 1024 atoms in a unit cell of LiCl-KCl system at 1123K.The error bars show the range of output data variations.

where hi indicates the time average,N(r,∆r)is the number of atoms within a spherical shell of r+∆r,N is the total number of atoms in the systems,ρ is the system number density,and V(r,∆r)is volume of the shell.

Figure 3 illustrates all RDFs of ion-pairs of Li+−Cl−,Li+−Li+,Li+−K+,K+−Cl−,K+−K+,and Cl−−Cl−in the LiCl-KCl system with 256 atoms in a unit cell at 1023K.The figure shows that Li+−Cl−and K+−Cl−pairs have the highest first peaks at the shortest distance.It indicates that they tend to aggregate together due to the attractive Columbic force between them.For the other ion pairs,since they have the same sign of charges,the repulsive force makes them more separation.However,all of them converge and fluctuate near g(r)=1 after a certain distance,that means they all reach molten state in equilibrium.

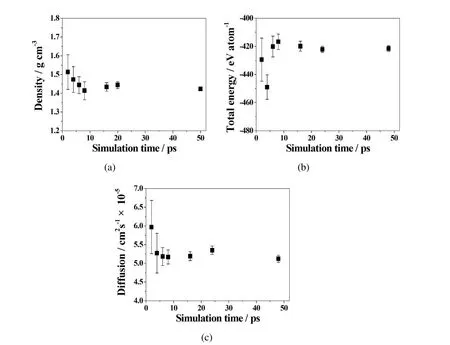
Figure 2:Convergence tests of(a)density,(b)total energy,and(c)diffusion coefficient,with different simulation time(2,4,6,8,16,24,and 48 ps,respectively)at the same time step of 2 fs in the LiCl-KCl system with 256 atoms at1123K.The error bars show the range of output data variations.

Table 2 outlines the structural parameters for LiCl,KCl,and eutectic LiCl-KCl molten salt systems in their RDF diagrams.In which rmaxis the position of the first peak;hmaxis the height of the first peak;rminis the position of the first minimum.Since it is difficult to measure such kind of structure parameters from experiments,we compare our results with some classical molecular dynamics simulation results published in existing literatures[Lantelme and Turq(1982);Caccamo and Dixon(1980)],although slightly under different simulation temperatures.The structural results are in good agreement in general,confirming the validity of the FPMD calculations.Introduction of the ionic polarization calculation in the FPMD simulation,whereby the Columbic repulsion and attraction are considered,may improve the simulation precision and accuracy.

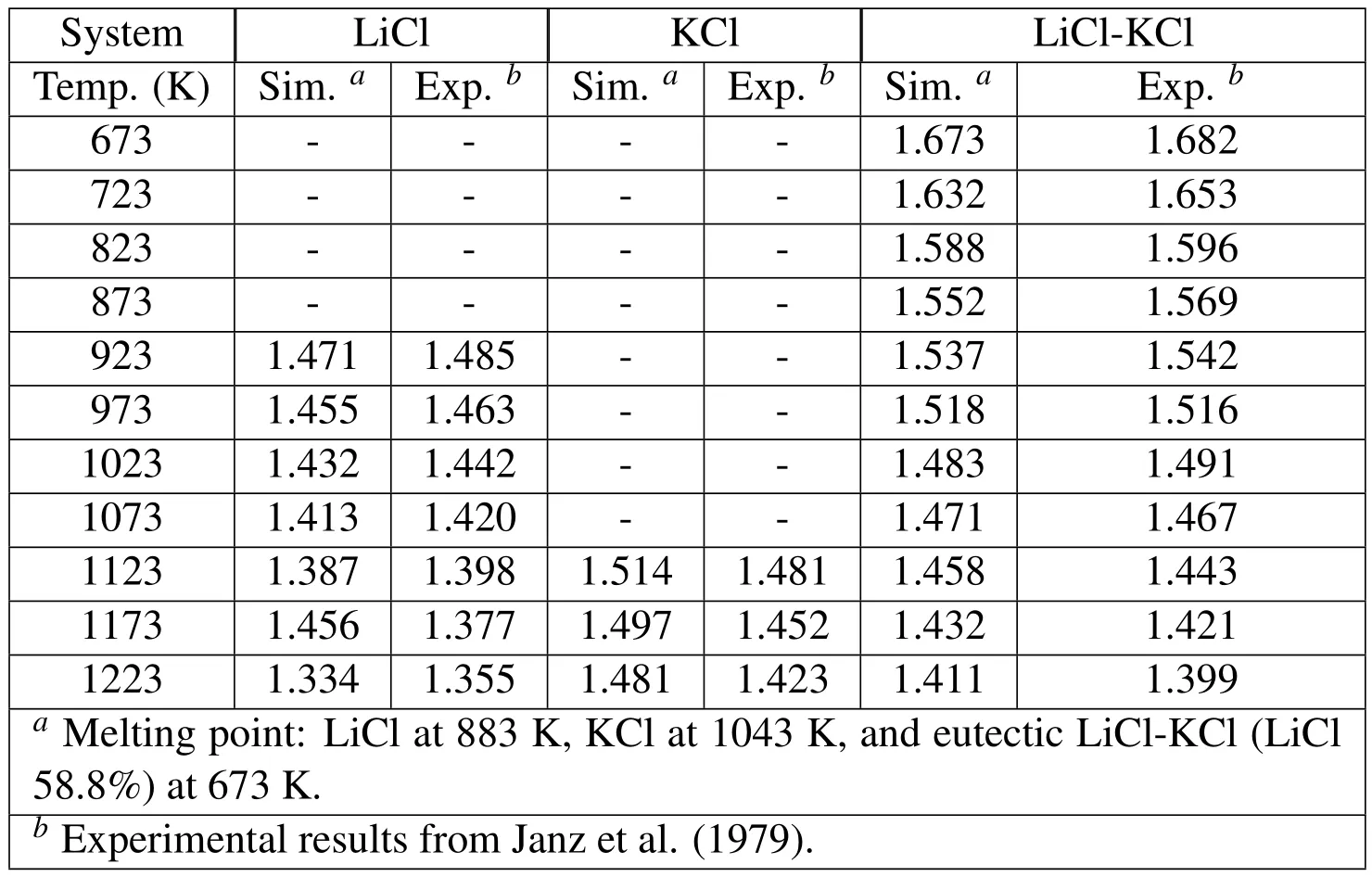
Table 1:Densities(g cm )of LiCl,KCl,and eutectic LiCl-KCl molten salts at various temperatures above their melting points.

3.3 Diffusion coefficient

The slope of the mean square displacement(MSD)versus time is related to the diffusivity of the activating ions,according to the Einstein expression:

whereDαis the diffusion coefficient of aα-type ion,δri(t)is the displacement in timet,and the angular brackets denote ensemble average over all the ions of speciesα.To investigate the temperature effect on the ionic diffusivity,we checked the diffusion coefficients of each ion in individual LiCl,KCl and eutectic LiCl-KCl

molten salt electrolytes at multiple temperatures.Since their melting points are different,so their operating temperature ranges are also different.Figure 4 and Figure 5 show that the FPMD simulation results predict almost linearly proportional effect of temperature on diffusion coefficients.Among all,the trend is that the higher the temperature,the greater the diffusivity.Also DLi＞DClin the LiCl and DK＞DClin the KCl system at the same temperature in Figure 4 and Table 3.In the eutectic LiCl-KCl system in Figure 5 and Table 3,it is DLi＞DCl＞DKin general.They are all due to the atomic mass effect,where Li＜ Cl＜ K,that the lighter the ion,the greater the diffusivity.

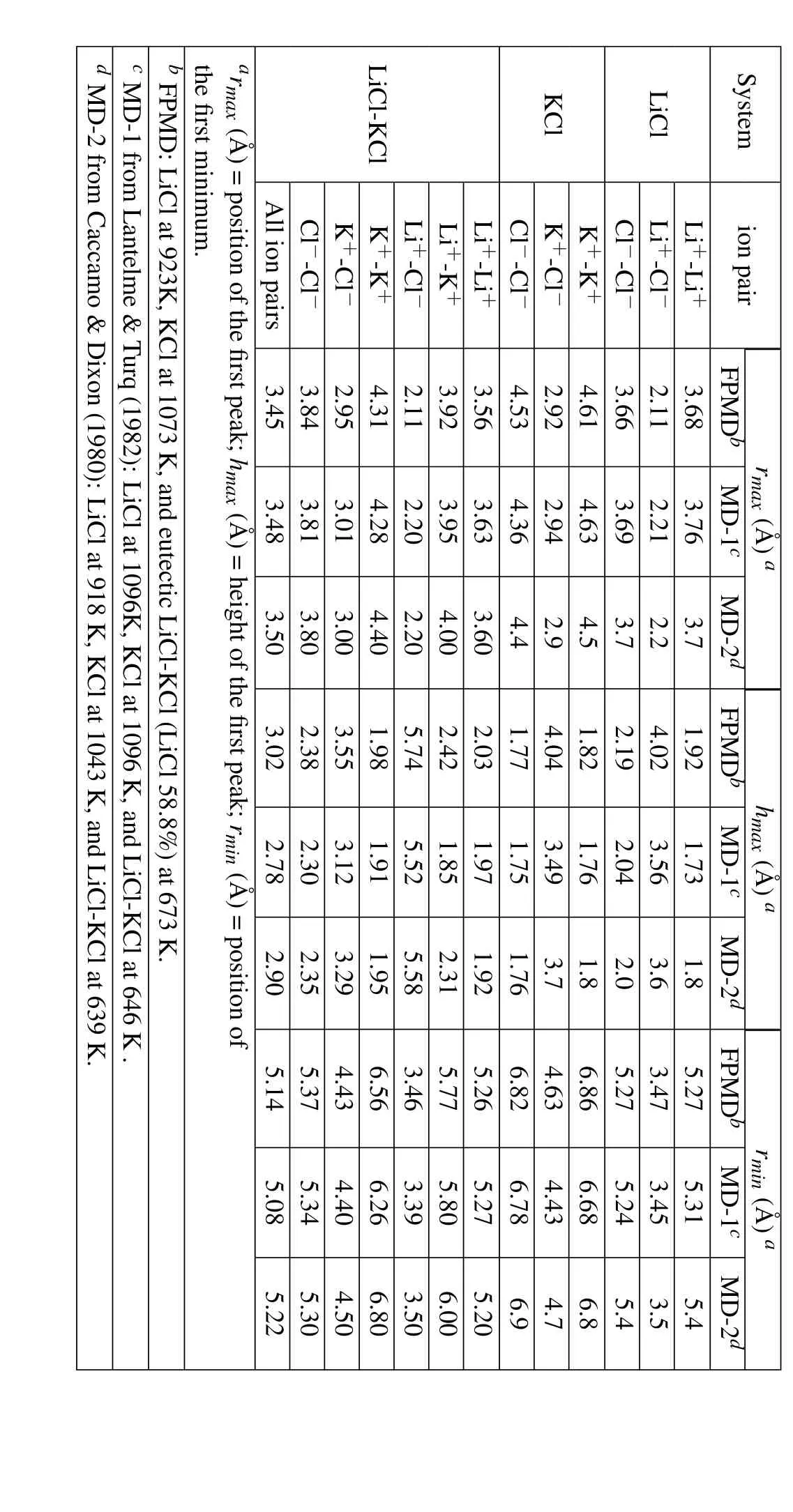
Table 2:Comparison of structural parameters for LiCl,KCl,and eutectic LiCl-KCl molten salts in their RDF diagrams.

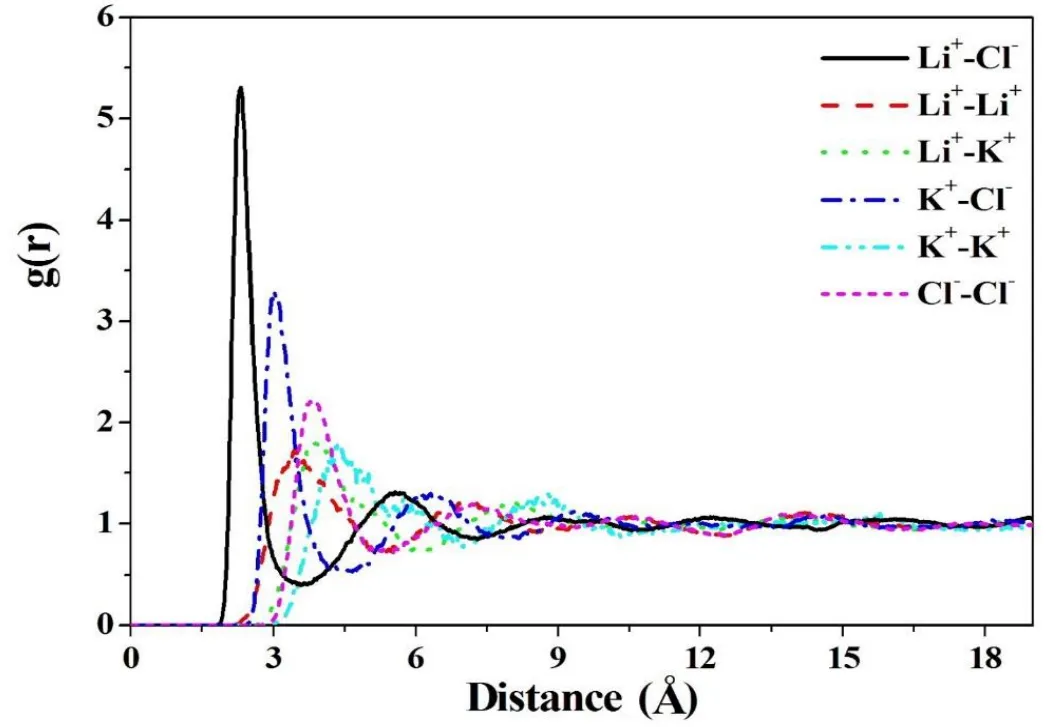
Figure 3:Radial distribution functions,g(r),of all ion-pairs in the LiCl-KCl system with 256 atoms in a unit cell at 1023K.

3.4 Ionic conductivity

Using the Green-Kubo(G-K)relation(Frenkel and Smit,1996),the ionic conductivity λ can be calculated from the time integral of the charge flux autocorrelation function through the FPMD method:

where V is the simulation cell volume,kBis the Boltzmann constant,T is temperature,and the charge flux vector JZ(t)is defined by in which zie is the charge of the ion,and viis the velocity of atom i.Each of the charge flux vector has three independent components(i.e.,JxZ,JyZ,JzZ),which provide an independent estimate of ionic conductivity in each direction.The averaged value(divided by 3)is taken as the overall ionic conductivity.

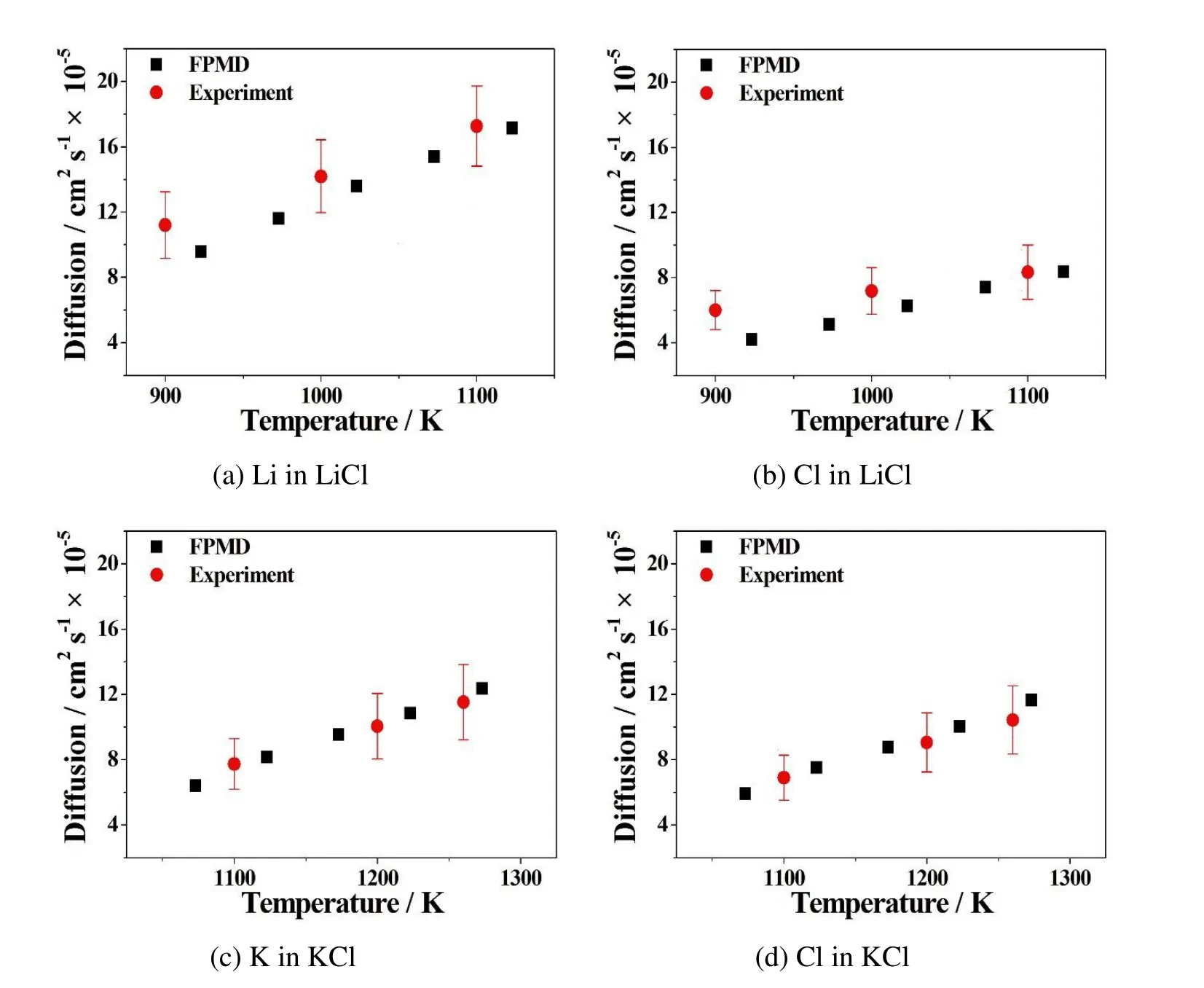
Figure 4:Comparison of FPMD simulation results with experiments on diffusion coefficients of(a)Li in LiCl,(b)Cl in LiCl,(c)K in KCl and(d)Cl in KCl at multiple temperatures.Black squares represent FPMD simulation results,and red circles are experimental results from Janz et al.(1979).The error bars show the uncertainties from the experiment,in which Li±20%,Cl±20%in the LiCl system and K±20%,Cl±20%in the KCl system.

Figure 6 compares the predicted ionic conductivity results of LiCl,KCl,and LiCl-KCl melts with published experimental data from Janz,Allen,Bansal,Murphy,and Tomkins(1979).Our FPMD approach slightly overestimates the experiments.However,the errors are more or less within the uncertainties of experiments indi-cated by the experimental report.Advanced investigation including the polarization effect should be able to improve the accuracy of the calculated results.Our FPMD calculations show that the ionic conductivities of molten salt electrolytes increase with increasing temperatures,same as the increasing diffusion coefficient accompanied by the rising of temperature.

Figure 5:Comparison of FPMD simulation results with other classical MD results on diffusion coefficients of ions of(a)Li,(b)Cl,and(c)K in the eutectic LiCl-KCl molten salt at multiple temperatures.Black square represent FPMD simulation results,cyan triangles are from classical MD-1[Lantelme and Turq(1982)],and purple stars are from another classical MD-2[Caccamo and Dixon(1980)].

3.5 Shear viscosity

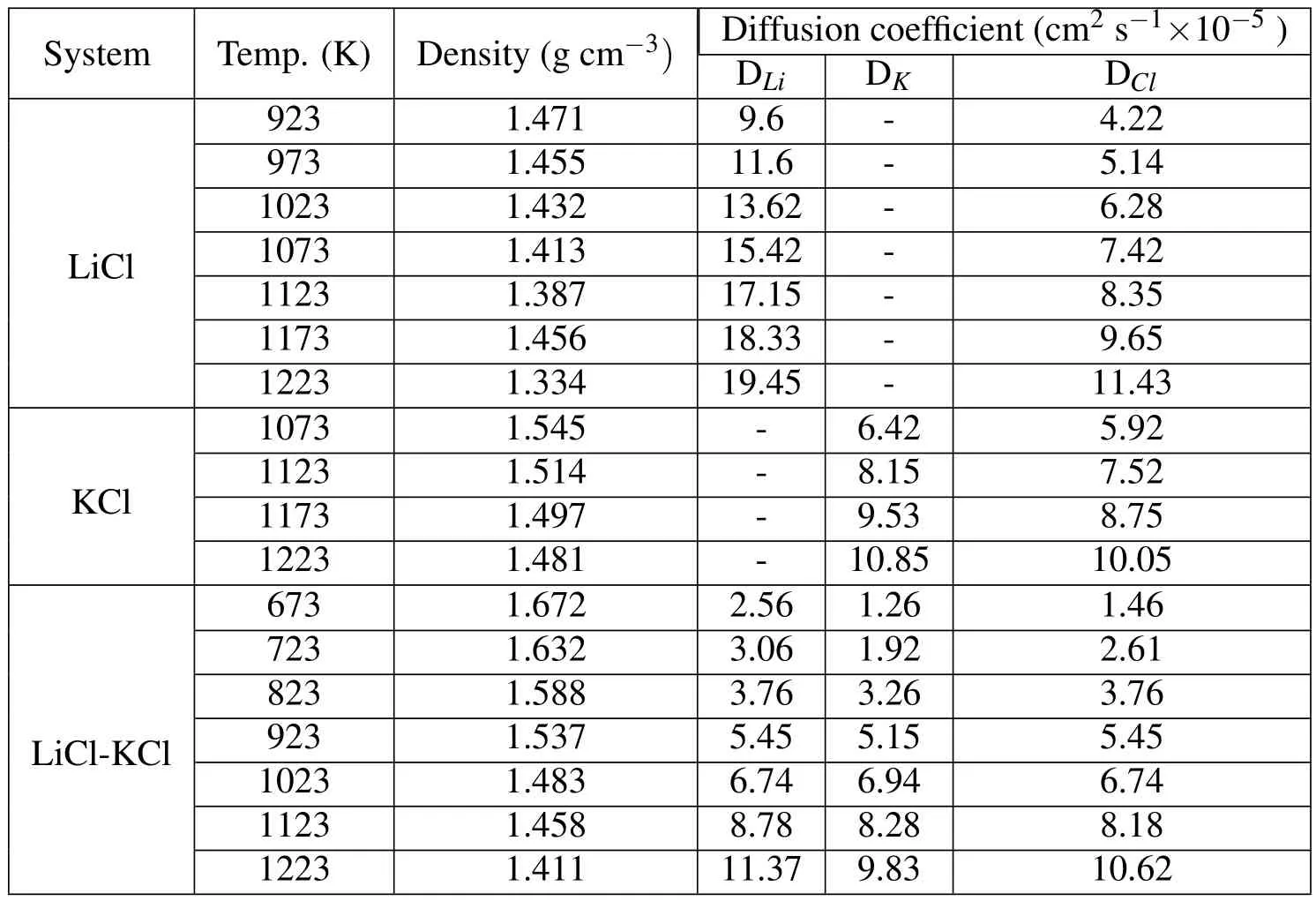
Table 3:Densities and diffusion coefficients of LiCl,KCl,and eutectic LiCl-KCl molten salts at multiple temperatures.

wherekBis the Boltzmann constant,Tis temperature,Vis the cell volume,andSxyis thexy-component of the stress tensor.Sxyis defined as

wheremiis the mass of ioni,vxiandvyiare thex-component andy-component ofvi(the velocity of ioni),xijis thex-component of distancerij=ri−rj,andfy(rij)is they-component of the forcefijon ionidue to ionj.Each of the independent offdiagonal components of the stress tensor(i.e.,Sxy,Syx,Sxz,Szx,SyzandSzy)gives an independent evaluation of the shear viscosity,and there are six off-diagonal terms,so the statistical precision can be improved by averaging over six that result from the stress tensor.

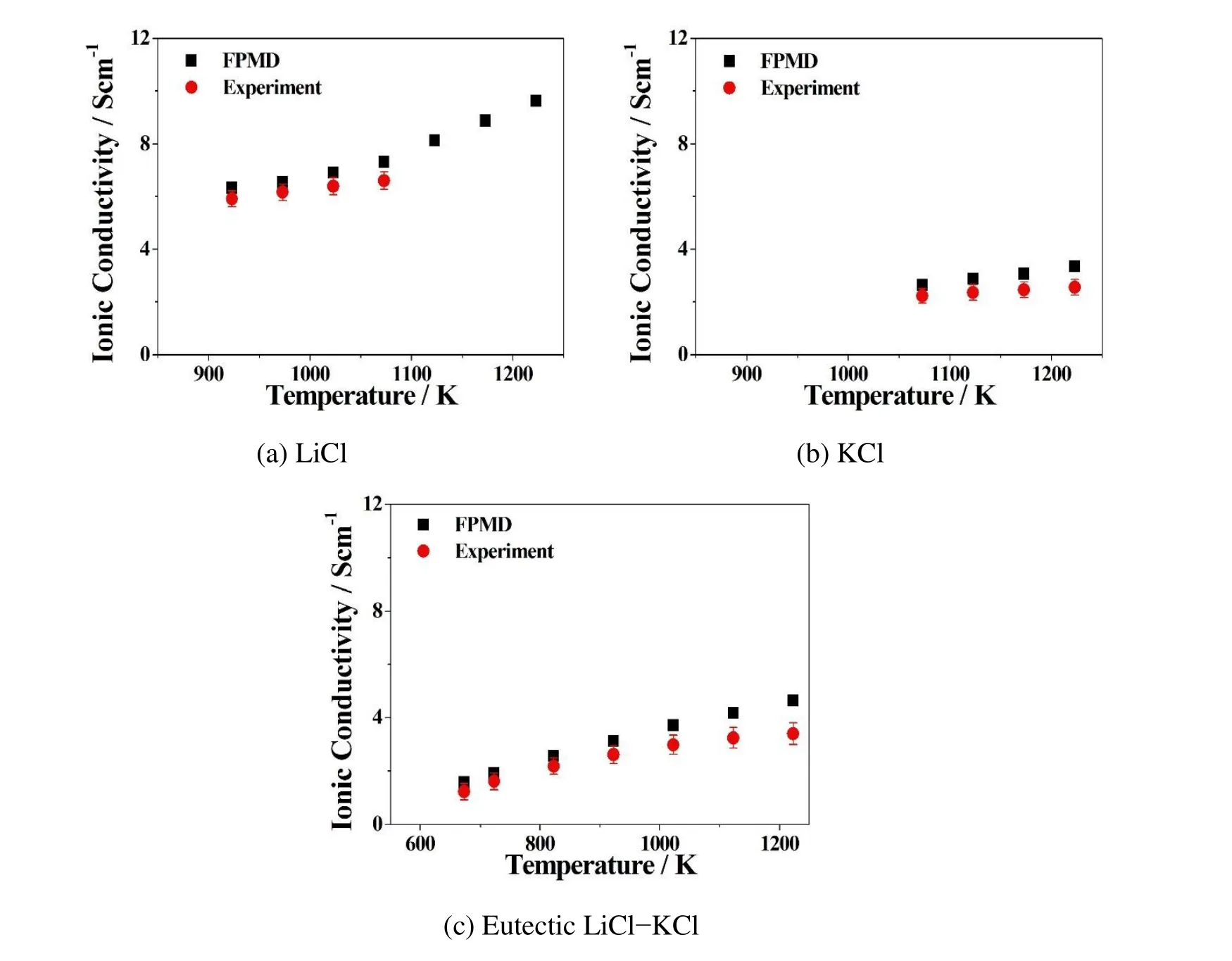
Figure 6:Comparison of FPMD simulation results with experiments on Ionic conductivities of(a)LiCl,(b)KCl,and(c)eutectic LiCl-KCl molten salts at multiple temperatures.Black squares represent FPMD simulation results,red circles are experimental results from Janz et al.(1979).The error bars show the uncertainties from the experiment,in which LiCl±2.5%,KCl±1.0%,and LiCl-KCl±2.5%when T＜1050K and LiCl-KCl±4.0%when T＞1050K.

The correlation function has been averaged over 1,000 time steps to ensure excellent statistics that repeated runs give the same platform value adequately.Shear viscosities of LiCl,KCl and LiCl-KCl molten salts have been calculated at multiple temperatures,above the melting point with an interval of 100 K.Figure 7 shows that they are in close agreement with experimental results form Janz,Allen,Bansal,Murphy,and Tomkins(1979).For LiCl and KCl systems,the predictions are under-estimated,but the errors are within the experimental uncertainties of±10%and±3%,respectively.For the eutectic LiCl-KCl,the calculation result-s are under-estimated below 900K and over-estimated when above 900K,but still within the experimental uncertainty of±15%.For LiCl,KCl,and LiCl-KCl molten salt systems,the shear viscosities decrease as the temperature increases,in contrast to the proportional trend of diffusion coefficients and ionic conductivities on temperature.

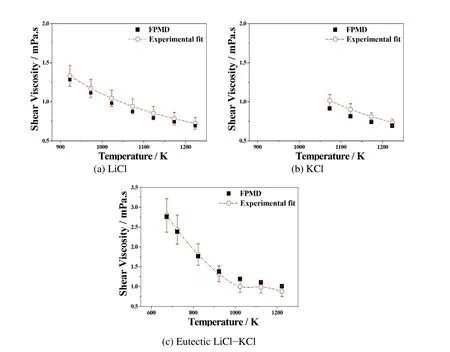
Figure 7:Comparison of FPMD simulation results with experimental fit on shear viscosities of(a)LiCl,(b)KCl,and(c)eutectic LiCl-KCl molten salts at multiple temperatures.Shear viscosities of(a)LiCl,(b)KCl,and(c)eutectic LiCl-KCl molten salt at multiple temperatures.Black squares are simulation results and red empty circles as well as their dashed dot lines are experimental fit from Janz et al.(1979).The error bars show the uncertainties from the experiment,in which LiCl±10.0%,KCl±3.0%,and LiCl-KCl±15.0%.

Figure 8:Comparison of FPMD simulation results with experiments on thermal conductivities of(a)LiCl,(b)KCl,and(c)eutectic LiCl-KCl molten salts at multiple temperatures.Black squares are simulation results,green triangles are experimental results from Nagasaka et al.(1992),and blue diamonds are from experiments carried out by Williams(2006).The error bars show the uncertainties from the experiment,in which LiCl±11.0%,KCl±5.0%,and LiCl-KCl±20.0%.

3.6 Thermal conductivity

The thermal conductivity κ can be calculated from the time integral of the energy flux autocorrelation function,based on the G-K formula

where kBis the Boltzmann constant,T is temperature,V is the simulation cell volume,JEis the energy flux,and JxEis the x-component of the energy flux vector.

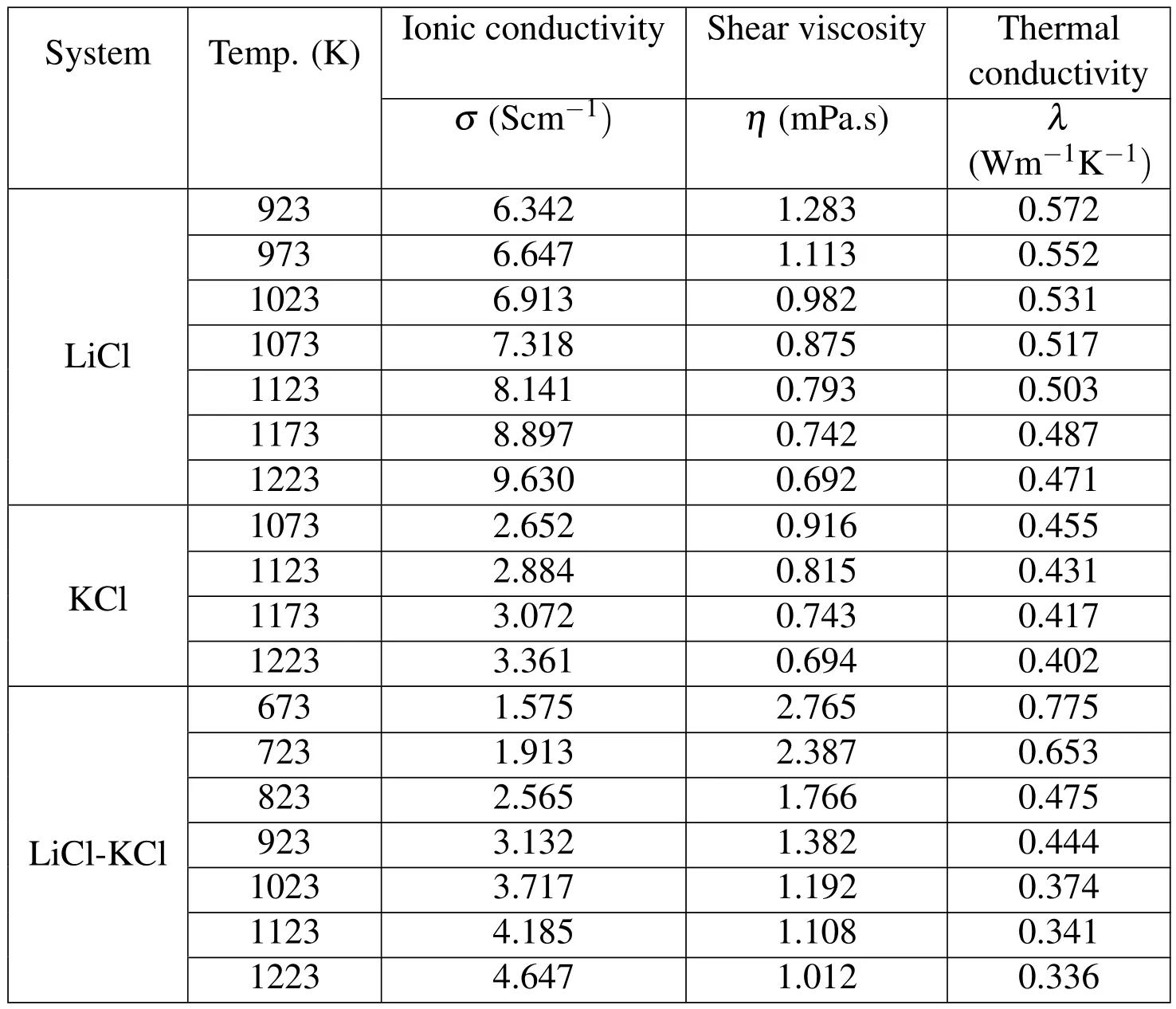
Table 4:Ionic conductivities,shear viscosities,and thermal conductivities of LiCl,KCl,and eutectic LiCl-KCl molten salts at various temperatures.

The energy flux vectorJEis defined as

and the energy per particleEiis defined as

(4)对于梁的加固，原有梁的混凝土强度不足，而且楼面又改为钢筋混凝土叠合层楼面，增大了梁的荷载，导致梁的承载力不足，因此对梁采用加大截面的方法进行加固。

wheremiis the mass of ioni,viis the velocity of the ioni,Uij(rij)is the pair potential between particlesiandj,rijis the position vector between particlesiandj,andfijis the force on ionidue to ionj.

Thermal conductivities of those molten salts have been calculated at multiple temperatures,above their melting points with an interval of 100 K.The calculation results are listed in Table 4 in detail.Figure 8 compares the simulated thermal conductivity values with those obtained from experimental data[Nagasaka Nakazawa,and Nagashima(1992);Williams(2006)]for single LiCl,KCl,and etuctic LiCl-KCl systems.All calculation results are within the uncertainties of experimental results,in which±10%for LiCl,±3%for KCl,and±15%for LiCl-KCl,respectively.The inversely proportional trend between the thermal conductivity and temperature is in accordance with experimental results.Table 4 also summarizes all the calculation results of transport properties,including ionic conductivities,shear viscosities,and thermal conductivities of LiCl,KCl,and LiCl-KCl molten salt electrolytes,which will be used to input to a commercial computational fluid dynamics(CFD)software to evaluate the macroscopic performance of a thermally activated battery.

4 Conclusions

An advanced first principles molecular dynamics(FPMD)simulation approach,based on the Hellmann-Feynman(HF)theorem,integrates the molecular dynamics simulation with the density functionaltheory(DFT)ofmulti-electron systems.This paperstudies the ionic structure and transportproperties(diffusion coefficient,ionic conductivity,shear viscosity,and thermal conductivity)in LiCl,KCl,and LiCl-KCl molten salts.In the preliminary convergence test,it has been proved that a unit cell of 216 atoms and simulation time of 16 ps are sufficient to achieve adequately converged results with acceptable accuracy.

The major advantage of the FPMD calculation technique is that it predicts the ionic interaction and transport properties without employing an empirical potential model,which is the major bottleneck of classical MD techniques.The calculation results can provide a well guidance when experimental measurements are difficult and costly to conduct.The predicted transport properties of LiCl,KCl,and LiCl-KCl molten salts are in good agreement with experimental results from published literatures.Diffusion coefficients and ionic conductivities are proportional to the operating temperature.However,shear viscosities and thermal conductivities of molten salts are proved to be inversely proportional to the rising temperature.

In summary,the single molten salt LiCl has a better ionic diffusivity,fluidity,and ionic conductivity than KCl.It is possible to improve the performance through addition of LiCl on the KCl.The eutectic LiCl-KCl has a much lower melting point than both LiCl and KCl,and the ionic conductivity is between them.All FPMD calculation results for LiCl,KCl and LiCl-KCl electrolytes are in close agreement with experiments in this paper.In the future,it is expected to develop a multi-scale simulation tool,including quantum mechanics,molecular dynamics,and computational fluid dynamics,to design a thermally activated battery from materials to the device.This is able to replace the costive trial-and-error experiments and to optimize the system design.

Acknowledgement:We thank the Ministry of Science and Technology in Taiwan and the National Chung-Shan Institute of Science and Technology for their support under the grant numbers MOST 103-2623-E-007-005-D.We are also grateful to the National Center for High-Performance Computing for the facilities made available to us.

Bengston,A.;Nam,H.O.;Saha,S.;Sakidja,R.;Morgan,D.(2014):Firstprinciples molecular dynamics modeling of the LiCl-KCl molten salt system.Computational Materials Science,vol.83,pp.362370.

Bradwell,D.J.;Kim,H.;Sirk,A.H.C.;Sadoway,D.R.(2012):Magnesiumantimony liquid metal battery for stationary energy storage.Journal of the American Chemical Society,vol.134,pp.1895-1897.

Brun,C.L.(2007):Molten salts and nuclear energy production.Journal of Nuclear Materials,vol.360,pp.1-5.

Caccamo,C.;Dixon,M.(1980):Molten alkali-halide mixtures:a moleculardynamics study of Li/KCl mixtures.Journal of Physics C:Solid State Physics,vol.13,pp.1887-1990.

Chen,C.F.;Li,H.Y.;Hong,C.W.(2015):Molecular dynamics analysis of hightemperature molten-salt electrolytes in thermal batteries.CMC-Computer,Materials,&Continua,vol.46,no.3,pp.145-163.

Cheng,C.H.;Lee,S.F.;Hong,C.W.(2007):Ionic dynamics of an intermediatetemperature Yttria-doped-Ceria electrolyte.Journal of The Electrochemical Society,vol.154,no.10,pp.E158-E163.

Cheng,C.H.;Chen,P.Y.;Hong,C.W.(2008):Atomistic analysis of hydration and thermal effects on proton dynamics in the Nafion membrane.Journal of The Electrochemical Society,vol.155,no.4,pp.B435-.B442.

Clark,S.J.;Segall,M.D.;Pickard,C.J.;Hasnip,P.J.;Probert,M.J;Refson,K.;Payne,M.C.(2005):First principles methods using CASTEP.Zeitschrift für Kristallographie,vol.220,pp.567570.

Eslamian,M.;Saghir,M.Z.(2012):Thermodiffusion applications in MEMS,NEMS and solar cell fabrication by thermal metal doping of semiconductors.FDMP:Fluid Dynamics&Material Processing,vol.8,no.4,pp.353-380.

Faraji,M.;Mustapha,E.A.;Mostafa,N.(2014):Numerical study of melting coupled natural convection around localized heat sources.FDMP:Fluid Dynamics&Material Processing,vol.10,no.2,pp.279-298.

Frenkel,D.;Smit,B.(1996):Understanding Molecular Simulation-From Algorithms to Applications,Academic Press,New York

Fujiwara,S.;Inaba,M.;Tasaka,A.(2011):New molten salt systems for high temperature molten salt batteries:ternary and quaternary molten salt systems based on LiF–LiCl,LiF–LiBr,and LiCl–LiBr.Journal of Power Sources,vol.196,pp.4012-4018.

Fukasawa,K.;Uehara,A.;Nagai,T.;Sato,N.;Fujii,T.;Yamana,H.(2012):Thermodynamic properties of trivalent lanthanide and actinide ions in molten mixtures of LiCl and KCl.Journal of Nuclear Materials,vol.424,pp.17-22.

Fumi,F.G.;Tosi,M.P.(1964):Ionic sizes and born repulsive parameters in the NaCl-types alkali halides-I the Huggins-Mayer and Pauling forms.Journal of Physics and Chemistry of Solids,vol.25,pp.31-43.

Galamba,N.;Costa Cabral,B.J.(2007a):First principles molecular dynamics of molten NaCl.The Journal of Chemical Physics,vol.126,pp.124502.

Galamba,N.;Costa Cabral,B.J.(2007b):First principles molecular dynamics of molten NaI:structure,self-diffusion,polarization effects,and charge transfer.The Journal of Chemical Physics,vol.127,pp.94506.

Galamba,N.;Nieto de Castro,C.A.;Ely,J.F.(2004):Thermal conductivity of molten alkali halides from equilibrium molecular dynamics simulations.The Journal of Chemical Physics,vol.120,pp.8676-8682

Galamba,N.;Nieto de Castro,C.A.;Ely,J.F.(2005):Shear viscosity of molten alkalihalidesfrom equilibrium and nonequilibrium moleculardynamicssimulations.The Journal of Chemical Physics,vol.122,pp.224501.

Galamba,N.;Nieto de Castro,C.A.;Ely,J.F.(2007):Equilibrium and nonequilibrium molecular dynamics simulations of the thermal conductivity of molten alkali halides.The Journal of Chemical Physics,vol.126,pp.204511

Guidotti,R.A.;Masset,P.(2006):Thermally activated(thermal)battery technology part I an overview.Journal of Power Sources,vol.161,pp.1443-1449.

Haimovich,N.;Dekel,D.R.;Brandon,S.(2009):A simulator for system-level analysis of heat transfer and phase change in thermal batteries I.computational approach and single-cell calculations.Journal of The Electrochemical Society,vol.156,no.6,pp.A442-A453.

Haimovich,N.;Dekel,D.R.;Brandon,S.(2015):A simulator for system-level analysis of heat transfer and phase-change in thermal batteries II.multiple-cell simulations.Journal of The Electrochemical Society,vol.162,no.3,A350-A362.

Hong,C.W.;Tsai,C.Y.(2010):Computational quantum mechanics simulation on the photonic properties of group-III Nitride clusters.CMES:Computer Modeling in Engineering&Sciences,vol.67,no.2,pp.79-94.

Hong,C.W.;Chen,W.H.(2011):Computational quantum chemistry on the photoelectric characteristics of semiconductor quantum dots and biological pigments.CMES:Computer Modeling in Engineering&Sciences,vol.72,no.3,pp.211-228.

Janz,G.J.;Allen,C.B.;Bansal,R.M.;Murphy,R.M.;Tomkins,R.P.T.(1979):Physical properties data compilations relevant to energy storage.II.molten salts data on single and multicomponent salt systems,National Bureau of Standards,U.S.Department of Commerce,New York.

Kohn,W.;Sham,L.J.(1965):Self-consistent equations including exchange and correlation Effect.Physical Review,vol.140,pp.11331138.

Kuhlmann,H.C.;Lappa,M.;Melnikov,D.;Mukin,R.;Muldoon,F.H.;Pushkin,D.;Shevtsova,V.;Ueno,I.(2014):The JEREMI-project on thermocapillary convection in liquid bridges.part A:overview of particle accumulation structures.FDMP:Fluid Dynamics&Material Processing,vol.10,no.1,pp.1-36.

Lantelme,F.;Turq,P.(1982):Ionic dynamics in the LiCl-KCl system at liquid state.The Journal of Chemical Physics,vol.77,no.6,pp.3177-3187

Masset,P.;Guidotti,R.A.(2007):Thermal activated(thermal)battery technology Part II.molten salt electrolytes.Journal of Power Sources,vol.164,pp.397-414.

Masset,P.;Henry,A.;Poinso,J.-Y.;Poignet,J.-C.(2006):Ionic conductivity measurements of molten iodide-based electrolytes.Journal of Power Sources,vol.160,pp.752-757.

Masset,P.(2006):Iodide-based electrolytes:a promising alternative for thermal batteries.Journal of Power Sources,vol.160,pp.688-697.

Masset,P.;Schoeffert,S.;Poinso,J.-Y.;Poignet,J.-C.(2005):LiF-LiCl-LiI vs.LiF-LiBr-KBr as molten salt electrolyte in thermal batteries.Journal of The Electrochemical Society,vol.152,no.2,pp.A405-A410.

Nagasaka,Y.;Nakazawa,N.;Nagashima,A.(1992):Experimental determination of the thermal diffusivity of molten alkali halides by the forced Rayleigh scattering method.I.molten LiCl,NaCl,KCl,RbCl,and CsCl.International Journal of Thermophysics,vol.13,no.4,pp.555-574.

Nevins,D.;Spera,F.J.(2007):Accurate computation of shear viscosity from equilibrium molecular dynamics simulations.Molecular Simulation,vol.33,no.15,pp.1261-1266.

Nosé,S.(1984):A unified formulation of the constant temperature molecular dynamics methods.The Journal of Chemical Physics,vol.81,pp.511-519.

San,C.H.;Chiu,C.P.;Hong,C.W.(2011):First principles computations of the Oxygen reduction reaction on solid metal clusters.CMC:Computers,Materials&Continua,Vol.26,no.3,pp.167-186.

San,C.H.;Hong,C.W.(2011):Molecular design of the solid copolymer electrolyte-poly(styrene-b-ethylene oxide)for Lithium ion batteries.CMC:Computers,Materials&Continua,vol.23,no.2,pp.101-118.

Srivastava,D.;Atluri,S.N.(2002):Computational nanotechnology:a current perspective.CMES:Computer Modeling in Engineering&Science,vol.3,pp.531-538.

Segall,M.D.;Lindan,Philip J.D.;Probert,M.J.;Pickard,C.J.;Hasnip,P.J.;Clark,S.J.;Payne,M.C(2002):First-principles simulation:ideas,illustrations and the CASTEP code.Journal of Physics:Condensed Matter,vol.14,pp.2717-2744.

Waldrop,M.M.(2012):Radical reactors.Nature,vol.492,pp.26-29.

Williams,D.F.(2006):Assessment of candidate molten salt coolants for the NGNP/NHI heat-transfer loop,ORNL/TM-2006/69,Oak Ridge National Laboratory,Oak Ridge,TN.

1Department of Power Mechanical Engineering National Tsing Hua University,Taiwan.

2Corresponding author.Tel:+886 3 5742591;Fax:+886 3 5722840;

E-mail:cwhong@pme.nthu.edu.tw