一维格点链上食饵—捕食者模型的蒙特卡洛模拟
一维格点链上食饵—捕食者模型的蒙特卡洛模拟
胡玉彪,乔文华
(包头师范学院物理科学与技术学院,内蒙古包头014030)
摘要:在一维格点链上定义了改进的两种群Lotka-Volterra模型,在只考虑近邻相互作用的情况下,分析了种群中每个生命个体的空间分布,及环境噪声对食饵—捕食者生命系统随时间进化的影响,利用蒙特卡洛方法,模拟计算了其动力学演化过程,给出了食饵—捕食者系统中两生命体能够长期共存,种群生态系统稳定的基本条件。
关键词:一维格点链;食饵—捕食者模型;环境噪声;蒙特卡洛模拟
收稿日期:2014-11-04
作者简介:胡玉彪(1988-),吉林省德惠市人,硕士研究生,研究方向:计算物理。
中图分类号:O186.13文献标识码:A
0引言
众所周知,生命现象的多样性决定了生态模型和生物数学的复杂性。当研究生命问题时,有许多因素会影响到生态模型的动力学性质,包括物种间的相互竞争,生存环境的变迁,人工的干预,突发性自然灾害的发生,都会对生物种群的生存与发展产生影响。正是由于生态系统的复杂性,需要借助于各种不同的数学模型来描述处在同一生态环境下不同生物种群间通过相互竞争,共生共存的自然现象。在描述由食饵-捕食者构成的两种群模型中,就有各种各样的数学模型[1-9],但是最基本的Lotka-Volterra[2,3]模型仍然是讨论这类问题的出发点,为此,我们首先对由Lotka-Volterra模型建立的数学方程作一个简要说明。由食饵-捕食者构成的两种群Lotka-Volterra非线性方程如(1)式所示
(1)
其中,a(t)是A(食饵)物种在时刻t的浓度,b(t)是B(捕食者)物种在时刻t的浓度,σ是物种A独立生存时的增长率,μ是物种B独自存在时的自然死亡率,比例系数λ1表示捕食者掠取食饵的强度(能力),比例系数λ2表示食饵的丰度(或食饵对捕食者的供养能力)。
对于标准的Lotka-Volterra模型,因为σ、μ、λ1和λ2都是常数,很容易得到食饵—捕食者种群浓度,具有持续震荡的准周期模式的数值解,但是,这样的结果往往被认为和实际的生态系统存在较大的差距[1,7,8]。认真分析其原因,我们认为由于λ1和λ2代表捕食者与食饵的相互作用,在自然情况下,发生捕食行为的过程中,捕食者掠取食饵的概率应该与食饵和捕食者的空间分布和相对位置有关。例如,某一时刻,一个食饵个体若处在捕食者的包围之中,此时它被捕食的可能性就高,反之,若食饵处在本物种的中央位置,它没有暴露在与捕食者的直接接触中,此时这个生命个体被捕食的可能性就很小;同理,某一时刻,若一个捕食者个体其四周近邻都有食饵存在,此时它捕获食饵的可能性就高,反之,若其四周近邻无食饵存在,此时这个捕食者捕获食饵的可能性就小很多。由于生活在同一空间区域里两个种群中的每个生命个体都在运动,随着时间的增长,它们会不断的移动到新的位置;更由于新生命体的产生、原有的某些生命体的死亡、以及被掠杀等现象的发生,必然使每个生命体自身的近邻不断变化,即其生态环境发生改变,所以,代表捕食者与食饵相互作用的λ1和λ2也应该不断随时间而变,任一时刻表示捕食者掠取食饵的强度λ1和表示食饵丰度的λ2应该根据该时刻的近邻条件计算和更新,而不该是一个恒定的数值。另一方面,自然环境、生态环境噪声的影响也是不可忽略的因素,因此,根据以上分析,我们将对两种群的Lotka-Volterra模型做出新的诠释,本文中,我们考虑在一维空间中,由食饵(A)和捕食者(B)构成的两种群系统中,每个生命个体所处空间位置对种群生存的影响,为使模型更接近于自然界的实际情况,我们将随机的给出生命个体的空间位置,然后在一定的演化机制下,用蒙特卡洛方法模拟其演化行为。
1一维格点链模型

(2)
考虑食饵种群(A)不受资源限制的一维链,初始时刻随机配置两种群个体的空间分布,考虑任意时刻tn时的两种群中每个生命体个体的空间分布,对第i个生命个体,只考虑最近邻相互作用的情况下:
(i) 若s(i)=0,且s(i-1)=0与s(i+1)=0,表示在第i格点位上有一个A物种的生命个体,且它的两侧近邻都是A物种,可以认为此刻它没有被捕食的风险。
(ii) 若s(i)=0,且s(i-1)=0而s(i+1)=1,或s(i-1)=1而s(i+1)=0,表示在第i格点位上有一个A物种的生命个体,而它的一侧近邻是A物种,另一侧近邻有B物种出现,它被捕食的可能性将比(i)增大,存在一定的风险。
(iii) 若s(i)=0,且s(i-1)=1与s(i+1)=1,表示在第i格点位上有一个A物种的生命个体,而它的两侧近邻都有B物种存在,它被捕食的风险最高。
(iv) 若s(i)=1,且s(i-1)=0与s(i+1)=0,表示在第i格点位上有一个B物种的生命个体,而它的两侧近邻都是A物种,提供给此捕食者的食饵丰度最大。
(v) 若s(i)=1,且s(i-1)=0而s(i+1)=1,或s(i-1)=1而s(i+1)=0,表示在第i格点位上有一个B物种的生命个体,它的一侧近邻是B物种,而另一侧近邻有A物种出现,提供给此捕食者的食饵丰度将比(iv)降低。
(vi) 若s(i)=1,且s(i-1)=1与s(i+1)=1,表示在第i格点位上有一个B物种的生命个体,它的两侧近邻都是B物种,提供给此捕食者的食饵丰度最低。
到下一时刻tn+1,由于捕食行为和种群间的相互作用,种群A和种群B中生命个体数量都发生改变,将要根据(2)式计算每个种群的个体数量(或浓度),并依照上述方法重新配置每个种群个体的空间分布。依此,可以计算系统在任意时刻的演化结果。
2蒙特卡洛模拟
2.1数据结构和初始条件
定义在时刻t,种群A生命体个数和种群B生命体个数占生物体总数的比率为pA(t)=nA(t)/N(t) 和 pB(t)=nB(t)/N(t)=1-pA(t),其中nA(t)代表A种群个体数,nB(t)代表B种群个体数,两种生物的总个数为N(t)=nA(t)+nB(t)。给定常数σ、μ的值,设初始时刻两种生物的总个数为N0,以及pA(0)=pB(0)=0.5,即有nA(0)=0.5N0个A种群个体,有nB(0)=0.5N0个B物种个体,它们随机的占据N0个格点位,设两种群各自的初始浓度a(0)=0.5、b(0)=0.5。
设在t时刻,已求得a(t)和b(t)及种群A和B中每个生命个体的空间分布,即A物种中的个体占据了nA(t)个格点位, B物种中的个体占据了nB(t)个格点位,两种群生命体的总个数为N(t)=nA(t)+nB(t), 共占据了N(t)格点位。
2.2模拟步骤
(1)逐次考察每一个格点位上生命体的自旋态,对第i个格点位上的生命体。
(i)若s(i)=0,且s(i-1)=0与s(i+1)=0,则令k1(t)=0×λ1。其中λ1是方程(1)中的比例系数,表示捕食者掠取食饵的强度(能力)。
(ii) 若s(i)=0,且s(i-1)=0而s(i+1)=1,或s(i-1)=1而s(i+1)=0,则令k1(t)=(1/2)×λ1×(0~1)。其中(0~1)表示取一个0到1之间的随机数。(下同)
(iii) 若s(i)=0,且s(i-1)=1与s(i+1)=1,则令k1(t)=(0~1)×λ1。
(iv) 若s(i)=1,且s(i-1)=0与s(i+1)=0,则令k2(t)=(0~1)×λ2。其中λ2是方程(1)中的比例系数,表示食饵的丰度(或食饵对捕食者的供养能力)。
(v) 若s(i)=1,且s(i-1)=0而s(i+1)=1,或s(i-1)=1而s(i+1)=0,则令k2(t)=(1/2)×(0~1)×λ2。
(vi) 若s(i)=1,且s(i-1)=1与s(i+1)=1,则令k2(t)=0×λ2。
(2) 考察遍历一维链上所有的N(t)个格点后,分别求出nA(t)个k1(t),及nB(t)个k2(t)的平均值



重复以上步骤(1)~(4)。
3模拟结果
图1、图2及图3是根据方程(2)的计算,给出了不同噪声、不同的反应速率(保持σ、μ不变,λ1、λ2取不同的值)情况下的结果,可以看出食饵浓度a(t)和捕食者浓度b(t)作为时间的函数在起始阶段有一个振荡过程,但是振荡的振幅随时间逐渐减弱,慢慢趋于平稳恒定的过程;从图中可以看出噪声越强,不但振荡衰减的越快,而且两生物种群最终保留的生命体数量也会受其影响,当噪声超过一定的强度(D≥0.001)时,对种群的生存产生不可逆转的影响,两种群都将随时间不断衰退,只至消亡。但是在相同的噪声强度下,较大的掠食系数λ1及食饵丰度系数λ2会使得这种衰退在一定程度上减弱,甚至使种群得以能够延续。这意味着在相互竞争和掠杀行为不断发生的过程中,两种群生命个体数量经历增长和死亡的振荡起伏,逐步趋向于增长和衰减互相平衡,每个种群中生命个体数趋于基本稳定,而较小的外界的各种干扰(噪声)有利于生态种群快速趋于某种分布“稳定”,较大噪声则会带来毁灭性的灾难;另一方面,较大的掠食系数λ1及食饵丰度系数λ2,代表食物的丰富和食饵种群数量的庞大,对于外界影响的抵御较强,所以迟缓了(或减弱了)噪声的作用,这是一种在外界环境因素干扰下,两种群系统自适应和自调整的过程。

图1

图2

图3
不同噪声强度下,食饵、捕食者浓度随时间的演化结果,红色线表示捕食者浓度b(t),蓝色线表示食饵浓度a(t),D为噪声强度(D=0表示无噪声)。
图4、图5及图6是食饵浓度和捕食者浓度在a-b平面内的轨迹,每幅图都描述了同一反应速率在不同的噪声下的相图(在同一幅图中的计算中我们使用了相同的λ1、λ2),从上述图中可以看出,当没有噪声或噪声较小时(D≤0.00001),食饵浓度和捕食者浓度在最初的振荡和涨落后,最终趋向于一个中心的固定点(数学上的焦点),这是一种稳定的结构,说明在此条件下食饵和捕食者两物种可以长期共存。但是当噪声较大时(D≥0.001),长时间的演化行为表明,不再能形成长时间的准周期振荡过程,在一个短暂的振荡涨落后(螺旋圈数明显减少),a(t)、b(t)很快就趋向于一个缓慢衰减区域,其在相平面内的轨迹不再稳定于数学上的焦点。
不同噪声强度下, 在a—b平面内的运行轨迹(相图),轨迹前进的正方向为逆时针方向, D为噪声强度(D=0表示无噪声)。

图4

图5

图6
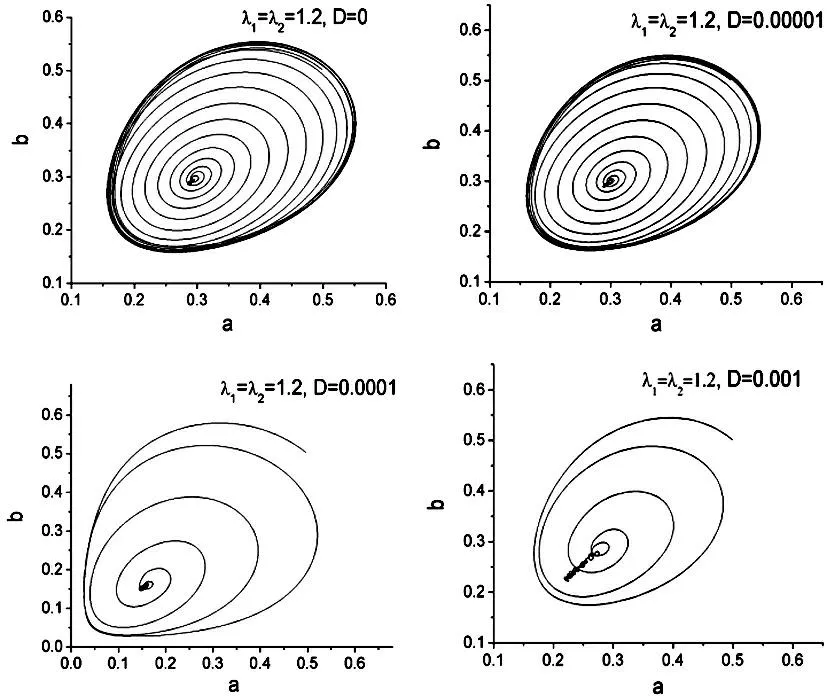
图7

图8

图9
4结论
参考文献〔〕
[1]Washerberger.M.J, Mobilia.M, T.uber.U.C. Influence of Local Carrying Capacity Restrictions on Stochastic Predator-Prey Models[J]. J. Phys. Condens. Matter,2007,19 (6):1088-1105.
[2]Lotka.A.J. Analtical. Note on Certain Rhythmic Relations in Organic Systems[J]. Biology,1920,6:410-415.
[3]Volterra.V. Lecons sur la. Theorie Mathematique De La Lutte Pour La Vie Redigees Par Marcel Brelot[J]. Book Review,1931,30:157-159.
[4]Javier.S, Tania.T. Stochastic Lattice Gas Model for a Predator-Prey System[J]. Phys. Rev. E,1993,49(10):5073-5079.
[5]Boccara.N, Roblin.O, Roger.M. Automata Network Predator-Prey Model with Pursuit and Evation[J]. Phys.Rev.E, 1994,50(6):4531-4541.
[6]Rozefeld.A.F, Albano.E.V. Study of a Lattice-Gas Model for a Prey-Predator System[J].Physica.A,1999,266(4):322-329.
[7]Lipowski.A. Oscillatory Behavior in a Lattice Prey-Predator System[J]. Phys. Rev. E.1999,60(5):5179-5184.
[8]Monetti.R, Rozenfeld.A, Albano.E. Study of Interacting Particle Systems: the Transition to the Oscillatory Behavior of A Prey-Predator Model[J].Physica.A.2000,283(2):52-58.
[9]Antal.T, Droz.M, Lipowski.A. Critical Behavior of a Lattice Prey-Predator Model[J]. Phys. Rev.E.2001, 64(3):1-6.
Monte Carlo Simulation of One-Dimensional Lattice
Chains Model for a Predator-Prey System
HU Yu-biao,QIAO Wen-hua
(Faculty of Physics and Technology,Baotuo Teachers College,Baotuo,014030)
Abstract:In one dimensional lattice chain we defines the improved Lotka-Volterr model of two populations,in the case of only considering the interaction neighbor,we study the spatial distribution of each individual life in population and the environmental noise of life how to effect on evolution of predator-prey system with time,by using Monte Carlo method,the dynamic evolution process are simulated,the predator-prey system is given in two organisms can co-exist for a long time and the population ecological basic conditions for the robust stability of the system.
Key words:One dimensional lattice chain;The predator-prey system model;Environmental noise;Monte Carlo simulation

