从“动静”角度看数学中的“动态”问题

■湖南省长沙市雅礼中学高三1318班　徐　戡



从“动静”角度看数学中的“动态”问题

■湖南省长沙市雅礼中学高三1318班徐戡

从辩证角度看，动与静是相对存在的.数学中“动态”问题的解决需要一定的想象能力，若其依据一定规律运动变化，则能更加考查学生的想象能力与分析能力了.不过，按照“一定规律运动变化”，则背后可能隐藏着不变的性质，我们称之为“静”，这一“静”便是我们解决问题的“题眼”，若能抓住这一“静”的本质或利用“动”“静”的相互转换，常能帮助我们突破思维的屏障、找准切入点、明确解题方向.课堂教学中出现“动态”类问题学生都感觉难以下手，本文想结合具体案例谈一谈解决这类问题常见的两种策略：动中觅静、以静制动，以及动静转换.下面让我们来看几个例子.

例1如图1，在长方形ABCD中，AB=2，BC=1，E为DC的中点，F为EC（端点除外）上一动点，现将△AFD沿AF折起，使平面ABD⊥平面ABC，在平面ABD内过点D作 DK⊥AB，K为垂足，设AK=t，则t的取值范围是________.

图1

分析：这个题目背景中，“静”的量是点运动轨迹所在的平面与直线垂直.那么能否作出这个平面呢？

解：如图2，过点D作DH⊥AF于点H，又DK⊥平面ABC，所以DK⊥AF，所以AF⊥平面DHK.（平面DHK就是我们所找的垂面）

图2

所以AF⊥HK.则点K相当于在原来长方形ABCD中，直线DH （DH⊥AF）与AB的交点，如图3.

图3

图4

解析：该题背景中的不变量为：①AB中点M到O的距离；②点M到点C的距离.所以1（当且仅当O、M、C三点共线时取等号）.

图5

例3如图5，已知正四棱锥V-ABCD可绕着AB任意旋转，AB⊂平面α.若点V在平面α上的射影为O，则|CO|的最大值为_________.

解析：如图6，设线段CD的中点为F，线段AB的中点为E，VE的中点为M，则该题中“静”的量为：；③棱锥侧面与底面所成角为60°（∠VEF=60°）.所以我们可以采取以下策略.

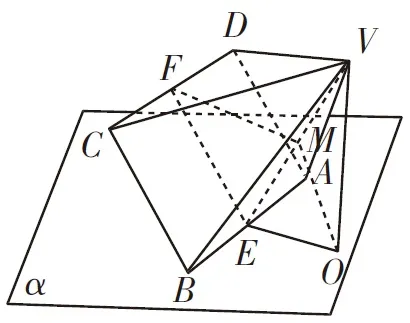
图6

评注：本题难点在于旋转过程中，点O和C都不定，很难找到突破口.策略一从运动中找不变的量入手，动中觅静，以静制动，这是解决这类问题的常用手段.要留心错解：|OC|≤|OM|+|MF|=3，此时等号取不到，因为O、M、E三点不可能不共线.策略二借助向量工具，活用向量分解，把已知向量分解为模或向量之间夹角确定的向量，化动为静，从而达到问题的轻松获解.

例4如图7，已知圆M：（x-3）2+（y-3）2=4，四边形ABCD为圆M的内接正方形，E为边AB的中点，当正方形ABCD绕圆心M转动，同时点F在边AD上运动时，的最大值是_________.

图7

评注：该思路把所求的向量分解转化为模或向量之间夹角确定的向量，以相对确定的向量来表示变化向量，从而减少运算量、思维量，达到化变化为不变，化动为静，以静制动的效果，使问题变繁为简.

运动和静止是相对的，运动的A相对于静止的B，也可看成B动A静，利用动静之间的这种相对性来解决“动态”数学问题常能收到出人意料的效果.

例5同例4.

解析：问题可看作正方形固定，原点O以M为圆心，以OM为半径做圆周运动，那么的最大值可以运用数量积的几何意义，借助图形（图8）易知，当O、M、 E三点共线，且点F在点A处时，向量在方向上投影最大，此时

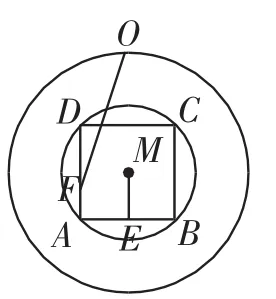
图8

评注：该问题按常规思维去解决会显得复杂，甚至束手无策，但换个角度，把多点运动转化为单点运动，脱掉复杂的外衣，使原问题难度大大降低，真是“山穷水尽疑无路，柳暗花明又一村”.

例6同例3.

解析：问题可看作四棱锥不动，平面α绕着AB转，则V在平面α上的射影为O的轨迹是以VE为直径的圆弧，且垂直CD（如图9），|OC|2=|OF|2+|CF|2≤

图9

评注：该思路运用运动的相对性，突破常规，反客为主，进行动静转换，体现出思维的灵活性和广阔性，把化归与转化及数形结合的思想运用得淋漓尽致，可谓妙哉！

数学问题因为变化而灵动，因为灵动而难以把握.所以在分析问题中，若能多考虑现象背后的本质，紧扣能支持这种变化的不变性，有意识地培养动中觅静、动静转换的策略，那么问题的解决便成为可能.F