由浅入深，自然形成——活动单导学模式下的以椭圆为例的性质探究

■江苏省白蒲高级中学　潘丹丹



由浅入深，自然形成——活动单导学模式下的以椭圆为例的性质探究

■江苏省白蒲高级中学潘丹丹

圆锥曲线是解析几何的重要内容之一，近几年圆锥曲线的综合问题涉及面广、运算量大，既考查了学生的思维能力，又考查了学生的运算能力.很多学生对这块的得分并不抱太大希望，其实这正是学生们能取得进步的一个突破口.

圆锥曲线有很多丰富精彩、生动有趣的性质，其定点、定值问题是诸多性质中的一条主线，而如何让学生从根本上记住这些结论以及运用这些结论是关键.事实上，仔细分析后我们发现，处理好圆锥曲线的这些问题的根本在于处理好与之相关的点.本文就以椭圆为例，如何由浅入深，一步一步引入并理解其性质及运用做一个思考.

活动一、基础自测

1.已知t∈R，圆C：x2+y2－2tx－2t2y+4t－4=0，若圆C过定点M，则定点M的坐标为_________.

2.圆O中，AB是它的一条直径，C是圆上异于A，B的任一点，则kCA·kCB=_________.

基础自测的目标是能够让所有学生都能去操作，明确学习目标，并体会到本节课所研究的内容.事实上，很多学生在做活动单的时候第一想法就是不管会与不会，拿到手就做，做之前和做完后也没有什么反思与总结.基础自测是预习内容中强调主干核心的知识，对知识的主干进行精确的梳理和科学的整合，加强知识与知识的内在联系，便于学生能有充分的主观认识.其形式以填空题的方式呈现，帮助学生进行知识的回顾.

基础自测第一题通过对无数个圆都过相同的点，特殊到两个圆的交点，然后验证这个交点就是研究的定点，以及通过无数个圆的认识体会到与变量无关，从而初步体现求定点问题的两种常见方法：

（1）利用曲线系（直线系）特征确定点或由特殊值确定一定点，再进行一般性证明；

（2）直接推理计算，并在计算推理过程中消去变量（与变量无关），利用方程组思想，从而得到定值.

事实上，这道题目也可以通过配方从形式上直接得到结论.

通过第三题，第四题对a2，b2及结论的关系，初步感受它们之间的内在联系，在授课过程中，从而提出疑问是巧合还是必然？明确研究目标，以椭圆为例，进而进行研究.

活动二、要点梳理

要点梳理是每张活动单知识核心的展现，是通过老师的传授，在学生理解的基础上展现出的知识核心，其过程展现方式有：

1.学生自我梳理.

通过对基础自测的完成以及学生对本节知识的自我回顾，借助于书本或者参考资料对知识体系加以梳理，其作用在于可激发学生自主的去学习，提升自我的归纳总结的能力.

2.老师与学生的共同提炼.

通过对题目的思路的分析，方法的总结，在学生理解的基础上，提炼出考查的相关知识点和结论.

对于本节课的知识梳理是：

（1）求定点及定值问题的常见方法：

①从特殊入手，求出定值，再证明这个值与变量无关；

②直接推理、计算，并在计算推理的过程中消去变量，从而得到定值.

（2）结论：

活动三、典型例题

典型例题是基础自测中题目的升华，通过经典例题能更深层次地展现本节课的知识核心，是学生能力展现，思维升华的展现.

例1已知椭圆C：，B为椭圆的上顶点，过点B的直线l1，l2与椭圆C分别交于点R，S（不同于B点），设直线l1，l2的斜率分别为k1，k2，若，求证：直线RS过定点，并求出此定点的坐标.

思路分析：本题研究直线RS过定点，只要求出直线的方程即可，关键在于通过联立方程组求出直线上R，S的两点坐标.

处理方式：在思路分析后，学生独立自主完成，小组讨论交流后，让学生通过黑板展示自我的成果.

解：由题可知，BR的直线方程为y=k1x+2，将直线与椭圆联立方程组

因为R，S关于原点对称，所以直线恒过定点（0，0）

注：本题在证明RS过定点（0，0）时，也可通过证明OR，OS的斜率相等.

教学过程中发现学生的思路清晰，方法明确，但在计算转化方面存在问题，由于圆锥曲线对于计算要求较高，笔者认为此题过程中在学生板书后应跟学生一起分析怎样求解，并鼓励学生加强学生的计算信心，为以后更复杂的计算打下基础.

为了进一步探究圆锥曲线中定点、定值的性质，笔者对此题做了一些变式：

思路分析：本题研究直线的斜率乘积，只要分别求出相对应的点即可，通过与学生共同分析分析可以发现，本题有两种不同的思路，思路一：可以选择设出直线方程后联立方程组求出点的坐标；思路二：可以根据点的对称性选择设而不求.

处理方式：在思路分析后，学生独立自主完成，通过投影展示，对比不同的思路.

方法2：设R（x，y），由椭圆的对称性可得S（-x，-y）.

通过对方法1和方法2的对比，让学生在掌握基本方法的同时能灵活运用一些解题的技巧将解题过程进行优化，进而提高解题的能力.很显然，若R，S为椭圆的左、右顶点，结论亦成立.

在变式1的基础上引导学生观察基础自测第三题，发现若R，S是左、右顶点，B是任意一点，探究一般性的结论，进而得到下面的变式：

学生通过自主探究得出一般性结论：

在授课过程中发现当学生在充分认识了结论1之后，有不少同学带有疑问，有同学就及时提出：如果在前面例题设而不求，利用对称性的基础上，如果保证R，S始终关于原点对称，B为异于R，S上任意一点，那结论还是否成立呢？此时，笔者自然而然提出下面的变式：

学生思考，独立自主完成，小组适当交流后，然后通过投影将成果展示.

显然结论1是结论2的特殊情况，在上述变式过程逐层递进，通过逆向思维引入变式1，通过变式1发现特殊情况，从特殊情况到一般情况，再研究一般情况.通过数形结合、归纳类比、设而不求的数学方法得到一般性的结论，并通过结论解决椭圆中与过原点弦的有关问题，以此来解决例2和变式.

图1

证明：设P（m，n），则A（-m，-n），C（m，0），所以kPA=，即，所以-1，即PA⊥PB.

建立在本节课所研究的基础上大大简化了这道题目的复杂性.事实上，不少同学在没有认知这个结论的时候，利用的方法就是将直线与椭圆联立方程组，通过方程组解出点的坐标，进而求出斜率，证明kPA·kPB=-1，对学生的运算能力和推理证明的能力较高，不少学生因为计算能力做到一半甚至就会打退堂鼓，当然上述结论在解答题中不能直接运用，需有证明的过程.

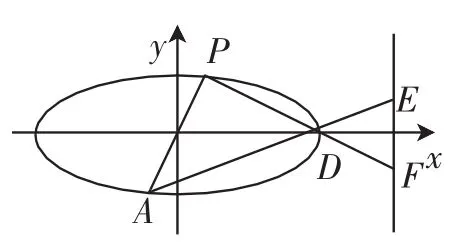
图2

解：由题意可知，直线AD的斜率存在且大于0，设kAD=k1＞0，则lAD：y=k1（x-2）.令x=3，得E（3，k1），由结论可得，所以令x=3，得F因为k1＞0，所以，当且仅当即时等号成立，所以|EF|的最小值为

活动四、课堂小结

活动单导学不仅重视学生获得知识的对与错，多与少，完成作业的优与劣，更关注学生的态度、情感、能力、责任心及合作精神等个性品质的培养，注重学生对过程的主体性体验，注重活动过程本身对学生的教育价值.事实上，在以椭圆为例的基础上探究了椭圆中与过原点弦的有关问题，通过类比的思想，可引导学生通过自主探究，自主学习，合作讨论去研究双曲线，抛物线中的类似结论.

在活动单导学的模式下，本节课中以“合作学习小组”为基本学习单位，以“自主、合作、探究”为主要学习方式，以“课堂反馈与评价机制”为保障，充分体现了“教为主导、学为主体、学会与会学、个性发展与全面发展”相统一的教学理念，以此培养学生的自主学习能力，探究问题的意识和合作学习的精神.