SMITH NORMAL FORMAL OF DISTANCE MATRIX OF BLOCK GRAPHS∗†

Jing Chen Yaoping Hou

(1.The center of discrete mathematics,Fuzhou University,Fujian 350003,PR China; 2.School of Mathematics,Hunan First Normal University,Hunan 410205,PR of China)

SMITH NORMAL FORMAL OF DISTANCE MATRIX OF BLOCK GRAPHS∗†

Jing Chen1,2‡, Yaoping Hou2

(1.The center of discrete mathematics,Fuzhou University,Fujian 350003,PR China; 2.School of Mathematics,Hunan First Normal University,Hunan 410205,PR of China)

A connected graph,whose blocks are all cliques(of possibly varying sizes), is called a block graph.LetD(G)be its distance matrix.In this note,we prove that the Smith normal form ofD(G)is independent of the interconnection way of blocks and give an explicit expression for the Smith normal form in the case that all cliques have the same size,which generalize the results on determinants.

block graph;distance matrix;Smith normal form

2000 Mathematics Subject Classification

1 Introduction

LetGbe a connected graph(or strong connected digraph)with vertex set{1,2,···,n}.Thedistance matrix D(G)is ann×nmatrix in whichdi,j=d(i,j) denotes the distance from vertexito vertexj.Like the adjacency matrix and Laplacian matrix of a graph,D(G)is also an integer matrix and there are many results on distance matrices and their applications.

For distance matrices,Graham and Pollack[10]proved a remarkable result that gives a formula of the determinant of the distance matrix of a tree depending only on the numbernof vertices of the tree.The determinant is given by detD=(-1)n-1(n-1)2n-2.This result has attracted much interest in algebraic graph theory.Graham,Hof f man and Hosoya[8]showed that the determinant of the distance matrixD(G)of a strong connected directed graphGis a function of the distance matrix of its strong blocks:

Theorem 1.1If G is a strong connected digraph with strong blocks G1,G2,···,Gr, then

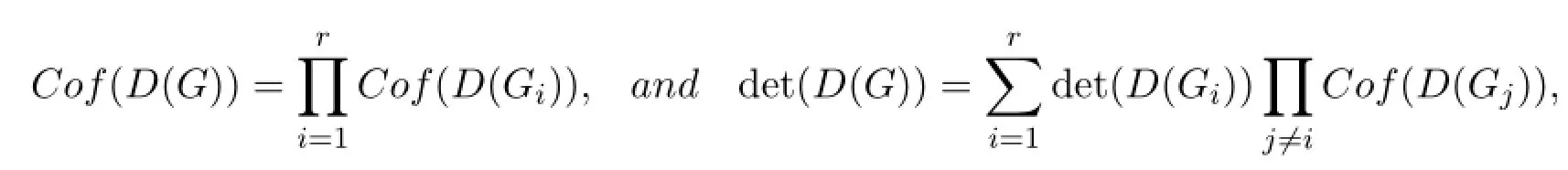
where Cof(A)is the sum of all cofactors of matrix A.

Graham and Lov´asz[9]computed the inverse of the distance matrix of a tree and studied the characteristic polynomial of the distance matrix of a tree.For more details about the distance matrix spectrum see[16]as well as the references therein.Almost all results obtained for the distance matrix of trees were extended to the case of weighted trees by Bapat et al.[2],and extended to the case that all blocks are cliques in[5,19].Extensions were done not only concerning the class of graphs but also regarding the distance matrix itself.Indeed,Bapat et al.[4] generalized the concept and its properties of the distance matrix toq-analogue of the distance matrix.Aouchiche and Hansen[1]investigated the spectrum of two distance Laplacian matrices.

For ann×ninteger matrixA,theSmith normal formofA,denoted bySnf(A),is ann×ndiagonal integer matrix

wheres1,···,snare nonnegative integers andsi|si+1(1≤i≤n-1)satisf i es that there exist invertible integer matricesP,Qsuch thatPAQ=S.Since detSnf(A)=|detA|and rank(Snf(A))=rank(A),the Smith normal form is more ref i ned invariant than(the absolute value of)the determinant and the rank.The Smith normal form of a matrix has some arithmetic and combinatorial signif i cance and was studied in arithmetic geometry[13],in statistical physics[7]and in combinatorics[3].There are also interpretations of the critical group in discrete dynamics(chip-f i ring games and abelian sandpile models[3]).For the Laplacian matrixL(G)of a graphG,the above group has been called the critical group(or sandpile group)of a graphG.And there are a few results on the Smith normal form of Laplacian matrix of a graph [12-14,17].For the results on the smith normal forms of other matrices of graph,see [6,20,21].

According to Theorem 1.1,the determinant of the distance matrix of graph does not change if the blocks of the graph are reassembled in some other way.Since the Smith normal form of a matrix is a ref i nement of determinant,the following question naturally arises.

Problem 1.1 Is the Smith normal form of the distance matrix of a connected graph independent of the connection way of its blocks?

In the case of a treeTonnvertices,the blocks are precisely the edge(K2,the complete graph on two vertices)and detD(T)=(-1)n-1(n-1)2n-2.In[11],it is shown that the Smith normal form ofD(T)is diag(1,1,2,···,2,2(n-1)),which isindependent of the structure of the treeT.

A graphGis calledblock graphif all blocks ofGare cliques.A tree and its line graph are block graphs.The aim of this paper is to extend the above result on trees to block graphs,also to prove the Smith normal form of the distance matrixD(G) of a block graphGis dependent only on the sizes of its cliques and to obtain the explicit expression of the Smith normal form of the distance matrixD(G)of a block graphGif all blocks have the same size.

2 The Smith Normal Forms ofD(G)for Block Graphs

In this section,we investigate the Smith normal form of the distance matrix for a block graph.We f i rst recall some concepts and computing methods about the Smith normal form of an integer matrix.Ann×ninteger matrixPis calledunimodularif|detP|=1.In other words,the unimodular matrices are precisely those integer matrices with integer inverses.Recall that twon×ninteger matricesAandBareunimodularly equivalent,and denoted byA～Bif there exist unimodular matricesPandQsuch thatPAQ=B.

It is well known that every integer matrixAis unimodularly equivalent to its Smith normal formS=diag(s1,···,sn)and the matrixSis unique and may be obtained fromAusing(integer)elementary row and column operations which are invertible over the ring of integers:

·swapping any two rows or any two columns;

·adding integer multiples of one row/column to another row/column;

·multiplying any row/column by±1.

Moreover,the productδi(A)=s1s2···siequals the nonnegative greatest common divisor(gcd)of all determinants ofi×i-submatrices ofA.s1,s2,···,snandδ1,δ2,···,δnare called theinvariant divisorsanddeterminantal divisorsofArespectively,see[18]for details.We can also obtain the Smith normal form of a matrix by the computation of determinantal divisors.

Considering the matrixAas a linear map Zn→Zn,itscokernelhas the form Zn/AZn.It is a f i nitely generated abelian group.By the structure theorem for fi nitely generated abelian groups,we have

(Of course,Z/1Z～=0 is the trivial group and Z/0Z～=Z.)We can also obtain the Smith normal form of a matrix by computing its cokernel.

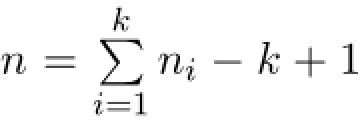
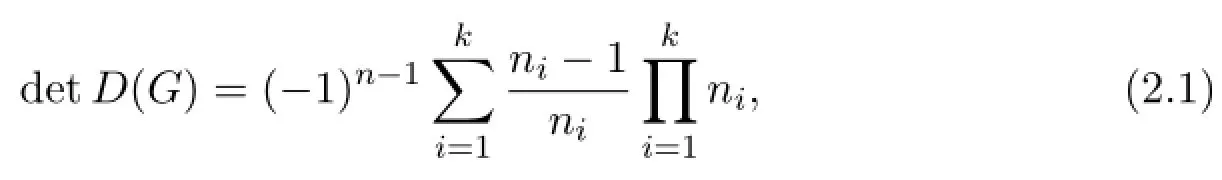
a formula depending only on the number of vertices of cliquesG1,G2,···,Gk,but not on the interconnection of these blocks.In this section we prove that the Smith normal form ofD(G)also depends only on the number of vertices of blocks,but not the interconnection of these blocks.

To do this,we need an elementary result on the Smith normal form of the integer matrixaI-bJ.

Let

Lemma 2.1Let Pn,Qnbe n×n matrices def i ned in(2.2),and a,b be integers. Then

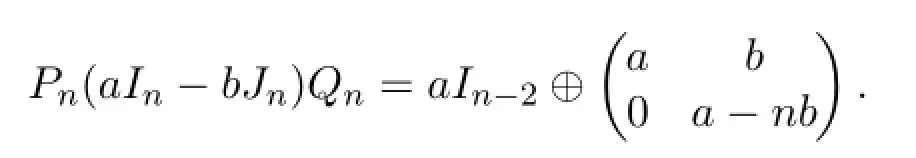
Hence,the Smith normal form of D(G)does not depend on the interconnection of the cliques.

Proof SinceGis a block graph with at least two blocks,it must have a leaf block (that is,the block contains only one cut vertex ofG).Without loss of generalization, suppose thatGkis a leaf block ofGand the vertexcis the unique cut vertex ofGinGk.LetDk-1be the distance matrix of the graphG-(Gk-c).Then the distance matrixDk=D(G)ofGcan be written as follows:

whereαis the column ofDk-1corresponding to the vertexc.Note thatα(c)=d(c,c)=0.Subtracting the row and column corresponding to the vertexcfrom the rows and columns ofGk-c,we get

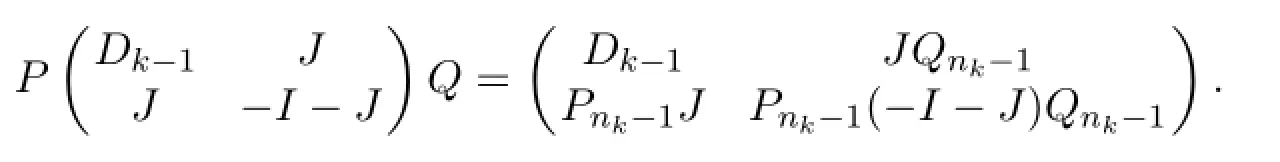
Since

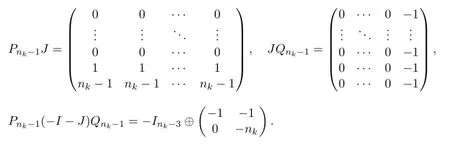
Thus

Subtracting the(n-1)-th column from then-th column and adding the(n-1)-th column to the columns 1,2,···,n-nk+1,we have

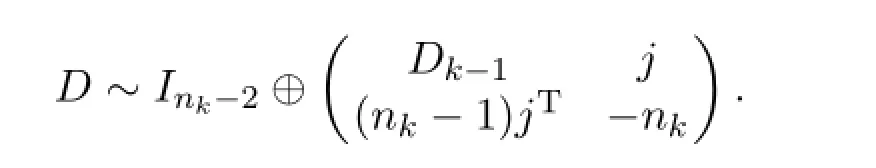
ForDk-1,continuing the above reduced way,we f i nally obtain

For the above matrix,subtracting the f i rst row and the f i rst column from the rows and columns 2,···,n1,we get

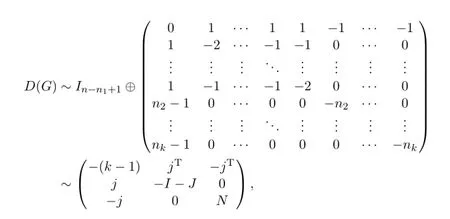
whereN=diag(-n2,-n3,···,-nk).

By some computation,we have

Although we can not give explicit formula of the Smith normal form of the (k+1)×(k+1)-matrix in Theorem 2.1 in general case,the next lemma is useful for the computation of its Smith normal form.

Lemma 2.2Let A(c0;b1,b2,···,bn;a1,a2,···,an)be an(n+1)-by-(n+1)integer matrix as follows:

where a1,a2,···,anare nonzero integers.For2≤r≤n,let U and V be nonempty subsets of{1,2,..,n,n+1}with|U|=|V|=r,and A[U|V]be the r×r-submatrix of A with rows in U and columns in V.Then:

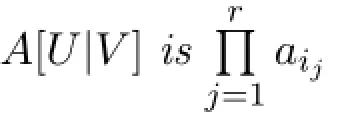
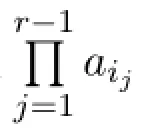
(3)If1∈U and1∈V,then

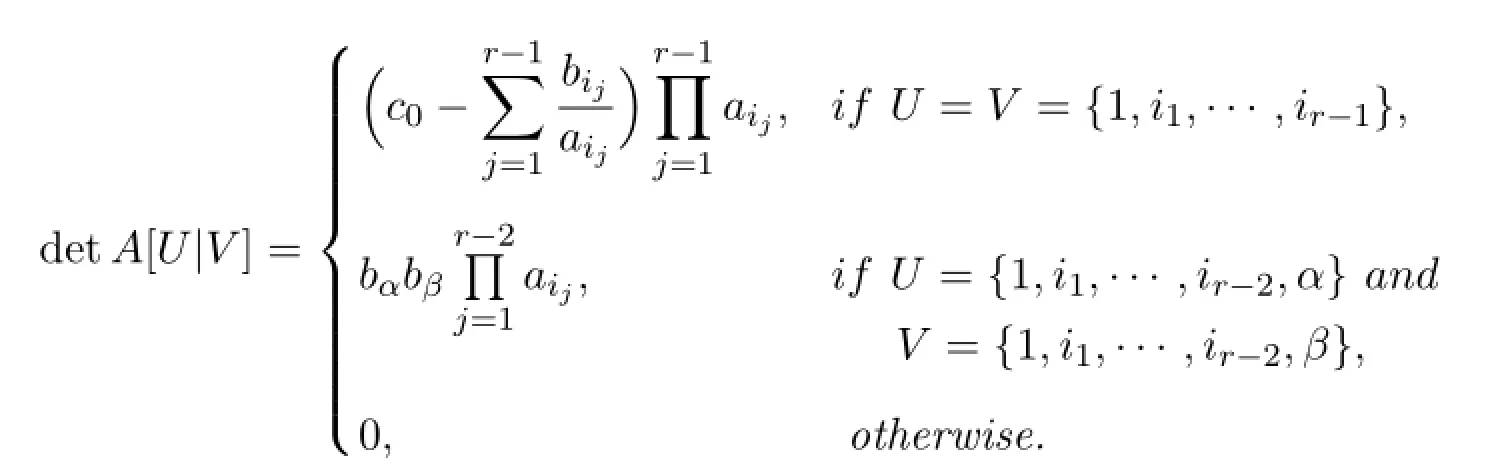
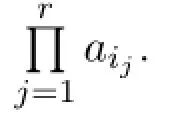
In case(2),without loss of generalization,assume that 1∈Uand 1/∈V={i1,i2,···,ir}.In order that the otherr-1 rows are chosen from{2,3,···,n,n+1}to yield anr×r-submatrix with nonzero determinant,we haveU-{1}⊂V.IfUcontainsx/=1 which is not inV,then rowxwill be all zeros in theA[U|V]and detA[U|V]=0.If indeedU-{1}⊂V,thenA[U|V]is of the form

In case(3),there are three subcases,depending upon howUandVintersect. If the symmetric dif f erence(U-V)∪(V-U)contains more than two elements, then one can check thatA[U|V]must contain a zero row or a zero column and detA[U|V]=0.

If(U-V)∪(V-U)={α,β},then one may assume thatU={1,i1,···,ir-2,α}andV={1,i1,,···,ir-2,β}.ThusA[U|V]is of the form

IfU=V={1,i1,i2,···,ir-1},then it is easy to check

The proof is completed.

Using Lemma 2.2,it is not difficult to obtain:

Corollary 2.1Let A=A(c;b,···,b;a,···,a)be a matrix of order n+1def i ned in Lemma 2.2.Then

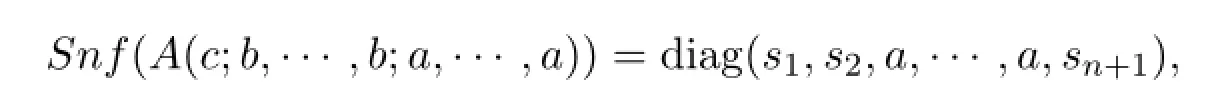
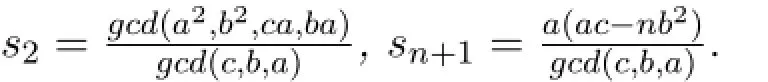
If all cliques of a block graphGhave the same size,then the Smith normal form ofD(G)has a simple form as follows.

Corollary 2.2Let G be a block graph with k cliques Kpand n=pk-k+1vertices.Then

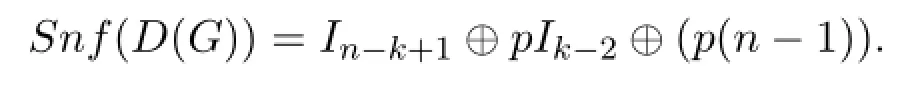
Proof By Theorem 2.1,D(G)is unimodular equivalent toIn-k-1⊕A(k;1,···,1;p,···,p).Applying Corollary 2.1,the Smith normal form ofA(k;1,···,1;p,···,p) isI2⊕pIk-2⊕(p(pk-k)).Sincen=pk-k+1,hence Corollary 2.2 holds.

[1]M.Aouchiche,P.Hansen,Two Laplcains for the distance matrix of a graph,Linear Algebra Appl.,439(2013),21-33.

[2]R.B.Bapt,S.J.Kirkland,and M.Neuman,On the distance matrices and Laplacians,Linear Algebra Appl.,401(2005),193-209.

[3]N.L.Biggs,Chip-f i ring and the critical group of a graph,J.Algebraic Combin., 9(1999),25-45.

[4]R.B.Bapt,A.K.Lal,and S.Pati,A q-analogue of the distance matrix of a tree,Linear Algebra Appl.,416(2006),799-814.

[5]R.B.Bapt,S.Sivasubramanian,Inverse of the distance matrix of a block graph,Linear Multilinear Algebra,59(2011),1393-1397.

[6]D.Chandler,P.Sin and Q.Xiang,The Smith normal critical groups of Paley graphs, arXiv:1401.8460v1.

[7]D.Dhar,Self-organized critical state of sandpile automaton models,Phys.Rev.Lett., 64(1990),1613-1616.

[8]R.L.Graham,A.J.Hof f man,and H.Hosoya, On the distance matrix of a directed graph,J.Graph Theory,1(1977),85-88.

[9]R.L.Graham and L.Lovasz, Distance matrix ploynoimal of a tree,Adv.Math., 29:1(1978),60-88.

[10]R.L.Graham,H.O.Pollack,On the addressing problem for loop switching,Bell System Tech.J.,50(1971),2495-2519.

[11]Yaoping Hou and Chinagwai Woo,Distance unimodular equivalent of graphs,Linear and Multilinear Algebra,56(2008),611-625.

[12]B.Jacobson,A.Niedermaier and V.Reiner,Critical groups for complete multipartite graphs and Cartesian products of complete graphs,J.of Graph Theory,44(2003),231-250.

[13]D.J.Lorenzini,Arithmetical properies of Laplacians of graphs,Linear and Multilinear Algebra,47(2000),281-306.

[14]D.J.Lorenzini,Smith normalform and Laplacians,J.Combin.TheoryB, 98(2008),1271-1300.

[15]C.Merino,The chip f i re game,Discrete Math.,302(2005),188-210.

[16]R.Merris,The distance spectrum of a tree,J.Graph Theory,14(1992),181-189.

[17]R.Merris,Unimodular equivalence of graphs,Linear Algebra Appl.,173(1992),181-189.

[18]M.Newman,The Smith normal form,Linear Algebra Appl.,254(1997),367-381.

[19]S.Sivasubramanian,q-Analogue of the distance matrices of 3-hypertrees,Linear Algebra Appl.,431(2009),1234-1248.

[20]P.Sin,Smith normal forms of incidences matrices,Sci.China Math.,56:7(2013),1359-1391.

[21]C.Williams,Smith forms for adjacency matrices of circulant graphs,Linear Algebra Appl.,443(2014),21-23.

(edited by Liangwei Huang)

∗This project was supported by the National Natural Science Foundation of China(No 11501188,11326057,11171102)and by Aid program for Science and Technology Innovative Research Team in Higher Educational Institutions of Hunan Province.

†Manuscript received

‡Corresponding author.E-mail:chenjing827@126.com