非线性微分方程三阶三点边值问题一个正解的存在性

郭丽君

(兰州交通大学博文学院 电信工程系, 甘肃 兰州 730101)

非线性微分方程三阶三点边值问题一个正解的存在性

郭丽君

(兰州交通大学博文学院 电信工程系, 甘肃 兰州 730101)

格林函数在三阶三点边值问题的正解存在性理论中有着重要作用.考虑以下三阶三点边值问题

三阶三点边值问题; 正解; 存在性; 锥; 格林函数; 不动点定理

三阶微分方程起源于应用数学和物理学等各种不同领域,有着广泛的应用背景和重要的理论价值.近年来,三阶三点边值问题受到了广泛的关注(见文献[1-8]).本文运用Guo-Krasnoselskii不动点理论研究了下列边值问题至少有一个正解的存在性准则

其中0<η<1,0<α<1/η,参数λ∈(0,∞).值得一提的是,文献[1]讨论了当边值问题(1)和(2)中参数λ=0时的特殊情况,通过运用Leggett-Williams不动点定理得到了边值问题(1)和(2)的3个正解的存在性.但文献[1]及文献[2-8]中相关的格林函数形式较复杂,没有得到更好的性质.本文的目的是进一步研究参数λ>0时的边值问题(1)和(2)正解的存在性,构造了新的格林函数,且形式上较简单,得到了新的性质,通过运用Guo-Krasnoselskii不动点定理,在非线性项f满足一定条件的情况下得到了边值问题(1)和(2)至少一个正解的存在性准则.

是全连续算子且下列条件之一满足:

(i) 当u∈K∩∂Ω1时,‖Au‖≤‖u‖且当u∈K∩∂Ω2时,‖Au‖≥‖u‖,

(ii) 当u∈K∩∂Ω1时,‖Au‖≥‖u‖且当u∈K∩∂Ω2时,‖Au‖≤‖u‖;

假设以下条件始终成立：

(C1)f∈C([0,+∞),[0,+∞));

(C2)a∈C([0,1],[0,+∞))且在[τ,1]上a(t)不恒为零,其中τ为(0,1)上的任意常数.

1 预备引理

为了得到本文的主要结果,需要以下3个重要引理.

引理 1 设0<α<1/η,则对于任意给定的y∈C[0,1],边值问题

u‴(t)+y(t)=0,t∈(0,1),

(3)u(0)=u″(0)=0,u′(1)-αu(η)=λ, (4)

有唯一解

其中

(5)

称为Green函数.

证明 事实上,如果u(t)是边值问题(3)和(4)的解,则可令

由u(0)=u″(0)=0,可得A=C=0.再由

u′(1)-αu(η)=λ,

可得

因此,边值问题(3)和(4)有唯一解

引理成立.

而在文献[1]中，当λ=0时边值问题(3)和(4)的格林函数为

形式上较复杂,且没有得到以下2个有用引理.

对本文格林函数(5),有如下2个引理:

引理 2 对任意(t,s)∈[0,1]×[0,1],有0≤G(t,s)≤1-s.

证明 首先考虑0≤s≤t的情况.此时

t(1-s)≤1-s.

如果t≤s≤1,显然有

0≤G(t,s)=t(1-s)≤1-s.

因此

0≤G(t,s)≤1-s, (t,s)∈[0,1]×[0,1].

引理成立.

引理 3 令0<η<1,0<α<1/η,则对任意(t,s)∈[τ,1]×[0,1],有G(t,s)≥γ(1-s),其中0<γ=τ/2<1,τ为(0,1)上的任意常数.

证明 如果0≤s≤t,则有

如果t≤s≤1,则有

因此,对任意(t,s)∈[0,1]×[0,1],均有

可令γ=τ/2,τ∈(0,1)为任意常数,则对任意(t,s)∈[τ,1]×[0,1]有

引理成立.

2 主要结果

在本文的剩余部分总是假定0<α<1/η,参数λ>0且条件(C1)和(C2)满足.标记

定理 2 假设下述条件成立：

(i)f0=0且f∞=∞(超线性);或者

(ii)f0=∞且f∞=0(次线性),

则边值问题(1)和(2)至少存在一个正解.

证明 设Banach空间E=C[0,1],赋予其范数

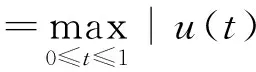
令

K={u∈E:u(t)≥0,t∈[0,1]且

显然K⊂E是锥.对u∈K,t∈[0,1]定义

(6)

由引理2可知,对任意t∈[0,1]都有

(7)

故

(8)

由引理3和(8)式可得,当t∈[τ,1]时有

因此

这表明AK⊂K.更进一步,容易验证A:K→K是全连续的且A的不动点即为边值问题(1)和(2)的解.

首先,考虑超线性情况:f0=0,f∞=∞,此时参数λ可足够小.

(9)

令Ω1={u∈E:‖u‖

(10)

因此由(10)式可知

‖Au‖≤‖u‖,u∈K∩∂Ω1.

另一方面,由于f∞=∞,则存在H2>H1,使得u≥γH2时有f(u)≥ρu,其中ρ>0且满足

(11)

令

Ω2={u∈E:‖u‖

则当u∈K,‖u‖=H2时有

u(t)≥γ‖u‖=γH2,t∈[τ,1],

因此由(11)式可得

所以

‖Au‖≥‖u‖,u∈K∩∂Ω2.

下面考虑对任意参数λ∈(0,∞)时的次线性情况:f0=∞,f∞=0.

由于f0=∞,则存在H3>0,使得0≤u≤H3时f(u)≥Mu,其中M>0且满足

(12)

则当u∈K,‖u‖=H3时,由(12)式可得

令Ω3={u∈E:‖u‖

‖Au‖≥‖u‖,u∈K∩∂Ω3.

由于f∞=0,则存在H>0,使得u≥H时,f(u)≤μu,其中μ>0满足

(13)

分以下2种情况考虑:

1) 假设f是有界的,即u∈[0,∞)时,f(u)≤N.此时可令

使得对任意u∈K,当‖u‖=H4时有

H4,t∈[0,1],

所以

‖Au‖≤‖u‖.

2) 如果f是无界的,可令

使得

f(u)≤f(H4), 0≤u≤H4.

(14)

则对任意u∈K,当‖u‖=H4时,由(13)和(14)式可得

因此

‖Au‖≤‖u‖.

所以,无论在哪种情况下,都可令

Ω4={u∈E:‖u‖

则对任意u∈K∩∂Ω4,都有‖Au‖≤‖u‖.由定理1的(ii)可知,边值问题(1)和(2)至少有一个正解.定理成立.

[1] SUN J P, GUO L J, PENG J G. Multiple nondecreasing positive solutions for a singular third order three point BVP[J]. Commun Appl Anal,2008,12:91-100.

[2] 孙建平,张小丽. 非线性三阶三点边值问题正解的存在性[J]. 西北师范大学学报(自然科学版),2012,48(3):29-31.

[3] 吴红萍. 一类非线性三阶三点边值问题的多个正解[J]. 贵州大学学报(自然科学版),2014,31(2):4-6.

[4] 张立新. 三阶边值问题的3个正解的存在性[J]. 四川师范大学学报(自然科学版),2011,34(4):466-470.

[5] 孙建平,曹珂. 一类非线性三阶三点边值问题正解的存在性[J]. 兰州理工大学学报(自然科学版),2010,36(2):123-124.

[6] 白婧,李永祥. 含一阶导数项的三阶周期边值问题解的存在性[J]. 四川师范大学学报(自然科学版),2015,38(6):834-837.

[7] 张立新,孙博,张洪. 三阶三点边值问题的两个正解的存在性[J]. 西南师范大学学报(自然科学版),2013,38(10):30-33.

[8] GUO L J, SUN J P, ZHAO Y H. Existence of positive solution for nonlinear third-order three-point boundary value problem[J]. Nonlinear Anal,2008,68:3151-3158.

[9] GUO D, LAKSHMIKANTHAM V. Nonlinear Problems in Abstract Cones[M]. New York:Academic Press,1988.

2010 MSC:34B15

(编辑 余 毅)

Existence of a Positive Solution for a Third-order Three-pointBoundary Value Problem of Nonlinear Differential Equations

GUO Lijun

(Department of Electronic and Information Engineering, Lanzhou Jiaotong University Bowen College, Lanzhou 730101, Gansu)

third-order three-point boundary value problem; positive solution; existence; cone; Green function; fixed point theorem

2016-01-22

甘肃省高等学校科研项目(2015B-214)

郭丽君(1980—),女,讲师,主要从事微分方程边值问题的研究,E-mail:5148806@qq.com

O

A

1001-8395(2016)06-0846-05

10.3969/j.issn.1001-8395.2016.06.013

其中,0<η<1,0<α<1/η,参数λ∈(0,∞).通过建立相关线性边值问题的格林函数得到解的形式,运用Guo-Krasnoselskii不动点定理建立上述边值问题至少一个正解的存在性准则.