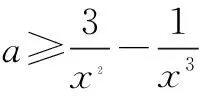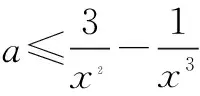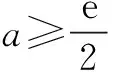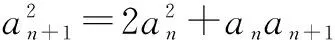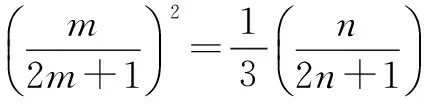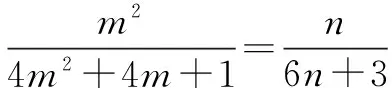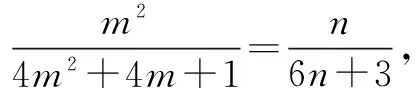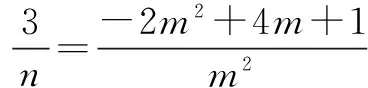问题与方法同在　思维携能力齐飞
——分离参数法习题课课堂教学及反思

丁金华

(江苏省新沂市高级中学，221400)

问题与方法同在思维携能力齐飞
——分离参数法习题课课堂教学及反思

丁金华

(江苏省新沂市高级中学，221400)

不等式恒成立背景下的求参数范围问题是求参数取值范围问题的重中之重,其为所有省份高考的命题热点.“数形结合法”、“分离参数法”是解决这类问题的基本方法,但学生在考试操作时总会遇到各种问题,非常有必要针对此处的细节进行深入分析．

一、问题提出

师:求参数范围问题是考试重点题型,但大家对于此类问题的处理思路不清晰、计算不准确、解题不规范.针对以上情况,这节课我们就此问题组织一节习题课,请首先探究以下数学问题．

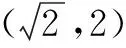
分组讨论大约5分钟,小组代表开始展示，并与老师交流.

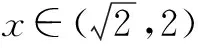
因为Δ=(2a2-2)2+8a2>0,结合图象,应有

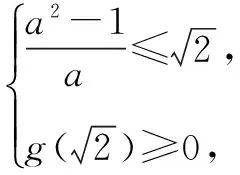
分别解上面两个不等组式,即可求得a的取值范围,但是我还没有解出最后结果．

师:以上是求参数范围问题时常用的“数形结合法”.生1思路清晰,表达准确,值得肯定,但是这样的解法运算较大,这也是生1没有给出最后结果的原因,请生1接下来继续完成本题．大家回顾,求参数范围还有什么其他更好方法?

生2:这类题最常用分离参数法,但是本题含有a2,参数不能直接分离出来,所以这种方法不适合用来解决本题．

师:能不能再想一想办法,设法将参数分离出来?

生3:可以将参数整体分离,例如，m2+m≥2sinx对x∈R恒成立,我们还是可以求出m的取值范围．

师:生3的想法很好,请大家接着尝试用整体分离参数法解决本题．

二、方法小试

生4:整体分离a，可得

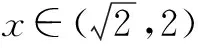
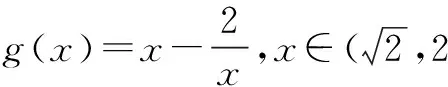
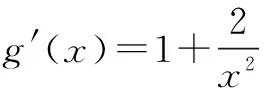
解之得0

师:生4分析问题深入,解决问题条理清楚，简单明了,值得表扬，请大家发表对以上解题过程的的体会．

生5:求参数范围时分离参数法有时看似不可用,但实际可能很高效,所以要勇于尝试,遇到困难时不能退缩，要有分离参数的意识．在实际解题时虽然参数可能含有平方项,但是可以整体分离,处理问题要灵活．

师(追问):结合之前处理恒成立问题的经验及本节课内容,请你们想想参数不好分离的情况还可能有哪些？

生6:参数的系数符号不确定,这时就不能直接分离,例如:mx≤2x2+1,x∈R 恒成立,求m的范围.分离参数时,不等号方向不能确定,怎么办？

三、思维发展

师:不等号的方向不确定时,我们可以通过分类解决这个问题,再试一试下面这道题．

问题2设函数f(x)=ax3-3x+1,若x∈[-1,1]时,f(x)≥0恒成立,求实数a的取值范围．

此题作为2008年江苏卷最后一个填空题,综合性强,涉及数学知识和数学思想方法多,有较高的训练价值,而且针对该题，教师已经充分预设,能启发学生想清楚,写明白,有利于优化的数学思维,提高学生的数学能力．

学生思考后开始展示:

生7:因为x∈[-1,1],所以可分三种情况讨论:

(1)若x=0,f(x)=1≥0恒成立；

综合(1)(2)(3)，可得a=4.

师:结合以上两题,请您们谈谈收获及感受(引导学生及时总结,反思)．

生8:分析问题时方法有了,但在题目特定环境下可能会遇到新问题,这时要改变思维方式,方法总比困难多．分离参数法是处理恒成立问题的重要方法,使用时遇到困难要想办法克服它,“狭路相逢勇者胜”,这不仅仅体现在求参数范围问题．

师:实际上,分离参数还有可能遇到新问题,这时我们需要的不仅仅是具体的“分离参数”法,而是“分离参数”解决问题的决心和能力．

问题3设f(x)是定义在x∈[-1,1]上的奇函数,函数g(x)与f(x)的图象关于y轴对称,且当x∈[0,1]时,g(x)=lnx-ax2.

(1)求函数f(x)的解析式;

(2)若对于区间(0,1]上任意的x,都有|f(x)|≥1成立,求实数a的取值范围.

师:本题的关键在于对|f(x)|≥1的处理,需要去掉绝对值符号,是采用平方法?还是使用绝对值定义?

生9:还是采用绝对值定义较好,平方太复杂．

师:好吧,你们赢了,接下来放手去做吧！

生10:(1)结合函数奇偶性,易知

(2)若对于区间(0,1]上任意的x,都有|f(x)|≥1成立,则

对任意x∈(0,1]，-lnx+ax2≥1恒成立,或者对任意x∈(0,1]，-lnx+ax2≤-1恒成立．

四、能力提升

师:由问题3可知,含绝对值不等式恒成立照样分离参数,在含有二元变量的方程有解问题,我们也可以借鉴这种思维分析、处理问题.也就是想办法分离其中一个变量,用另一个变量表示,结合题目其他条件,判断方程有无解或者解出两个变量值．

(1)求数列{an}的通项；

生11:(1)an=2n(具体过程此处省略)．

若b1,bm,bn成等比数列,则

但是接下来就不知改如何处理了．

师:提示一下,此时的n分离到位了吗?如果没有,就还可以再往下面走一走,该如何走下去?

所以-2m2+4m+1>0, 从而

又m∈N*,所以m=2,此时n=12,经验证m=2,n=12满足题意．

师:很好,对n的分离一定要到位,这时问题就容易解决了,看来分离参数不仅仅是数学方法,更是数学思想、数学能力.上述一系列解题过程,看似“新奇”,实则“平凡”,关键在于处理问题时做到“因果关系清晰,推理有理有据,表达层次清楚,结果完整无缺”．

五、教学感悟

1.学生的数学思维只能在数学活动中得到发展

数学问题作为促进学生思维发展的重要载体,可以开发潜能,暴露不足,促进学生思考模式不断完善,一定程度上,数学课堂就是解决一个个数学问题的过程．要善于设计知识与方法“生长点”上的问题,以问带思、以问带练,通过解决数学问题的数学活动,促进学生感受数学的抽象、严谨,认识到可以从多角度分析问题、多层次解决问题.在数学活动中,学生的认知结构会经历冲击、碰撞、重组,完成重新自我建构,这个时候数学思维自然而然的就发生和发展了．本案例“问题导学、合作探究”,教师恰当地设计路标,导航引路,促进学生积极参加到数学活动中去,学生在活动中探索解题思路,探求解题结果,感受到了思维受阻的苦闷,更享受了解题成功的喜悦,在一次次的头脑风暴中发展了数学思维．数学思维的发展离不开数学活动,数学活动效果的呈现关键在数学问题的设计．

2.学生的数学能力在数学探究中才能生长

“课堂要呈现的不仅仅是鲜花,还应该有鲜花绽放的过程”.在数学课堂上,我们不仅仅要数学结果,更需要的是在结果出现过程中的数学体验及思维过程,那恰恰是数学能力生长的关键．高三阶段的复习课,很多老师组织教学的原则是“将题目讲透”.他们努力将题目的来龙去脉,方法思路、一题多解、变式训练统统告诉学生,学生只需坐享其成,“带着眼睛、耳朵欣赏就够了”,学生的参与仅仅是记笔记．他们认为这样的解题教学能节约时间,提高效率,只要课堂总结到位、练习跟踪到位,学生的数学解题能力自然就有了.就这样,老师没少讲,学生没少练,但效果一点也不明显.实际上,在高三备考复习中,教师要关注的不是讲题的多少,更不是解题方法是否精彩,变式训练是否到位,要关注的是在解题教学中学生参与探究活动时间及深度,如何给学生恰到好处的引导,使他们的数学思维及数学探究合理地展开和进行.不能剥夺学生独立思考和合作探究的机会,要让学生积极尝试、合理探索．本案例中学生经历了“运算的困扰”,尝试了“方法的多样”,感受了“逻辑的严密”,体验了“触类旁通的感觉”,一节课共涉及4个数学问题,没有一个题目是老师“讲会的”,而是老师提供机会,让他们“悄悄地,不知不觉就会了”.经历本节课的探索过程,学生掌握的的不仅仅是这四个数学问题,还有很多很多．学生数学能力的生长,数学探究是关键,要努力给学生提供数学探究的机会,这不仅仅体现在高三复习课上，而且应当贯穿于整个高中数学教学中．