含梯度项的椭圆方程组的边界爆破解
李华,马飞遥
(宁波大学理学院,浙江 宁波 315211)
含梯度项的椭圆方程组的边界爆破解
李华,马飞遥
(宁波大学理学院,浙江 宁波315211)
研究了含梯度项的椭圆方程组的边界爆破解的性质,其中权函数a(x),b(x)为正并且满足一定的条件.利用上下解的方法及比较原则证明了正解的存在性与唯一性,并得到了边界爆破速率的估计.
椭圆方程组;梯度项;边界爆破
1 引言
主要考虑如下的含有梯度项的椭圆方程组:

其中 λ,t>0,p,s>1,q,r<0,(p-1)(s-1)-qr>0,Ω∈RN为一个有界光滑的C2区域.a,b∈Cη是非负权函数,η∈(0,1).边界条件u=+∞,v=+∞,x∈∂Ω,表示当d(x)→0+时,u(x)→∞,v(x)→∞,其中d(x)=dist(x,∂Ω).
当λ=t=0时,方程组变为

此方程组已在文献[1-3]中被广泛研究.其中Meli´an在文献[1]中研究了a(x)=b(x)=1这种特殊情况下,方程组在三种不同的Dirichlet边界条件:(F)u=λ,v=µ,(I)u=v=+∞与 (SF)u=+∞,v=µ下,在 ∂Ω上解的定性性质.在文献 [1]中又进一步的考虑了带权函数的方程组 (1.2),给出了当 d(x)→ 0时,在条件 a(x)∼C1d(x)γ1,b(x)∼C2d(x)γ2,C1,C2>0,γ1,γ2>-2下解的存在性与不存在性,唯一性及边界性行为的结果.文献[2]Meli´an对系统(1.2)又进行了研究给出了不同于文献[1]的唯一性的证明.
文献[4-5]对拟线性的椭圆系统的边界爆破解进行研究,得到了解的存在性,唯一性及边界爆破行为.
对于单个的含梯度项的椭圆方程 ∆u±λ|∇u|q=b(x)g(u),x∈Ω;u=+∞,x∈∂Ω. C.Bandle 1996年在文献 [6]中对 λ=1的形式进行了详细研究.文献 [7]张志军应用了Karamata正规变换理论,得到了方程解的唯一性与爆破行为.含梯度项的椭圆方程更深入的研究参见文献[8-10].
本文考虑的是含梯度项的椭圆方程组,首先定理2.1改变了文献[7]定理1.1的条件,应用文献[7]中同样的技巧Karamata正规变换理论与比较原则,得到了单个方程爆破解的渐进性结论.其次,在对单个方程研究的基础上,利用上下解的方法证明了当(p-1)(s-1)-qr>0时方程组(1.1)解的存在性,利用迭代思想得到了解的爆破速率估计,并给出了在一定的条件下解的唯一性的证明.要求权函数满足以下条件:
假设a,b∈Cη,η∈(0,1),存在γ1,γ2>-2与正常数C1,C2,C′1,C′2,使得

下边给出本文的主要结论:
定理 1.1假设 p,s>1,q,r<0,a(x),b(x)∈Cη,η∈(0,1)且满足条件 (1.3),则当(p-1)(q-1)>qr时,方程组存在正解.方程组的解(u,v)满足:
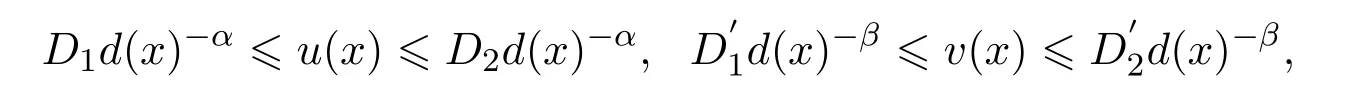
其中
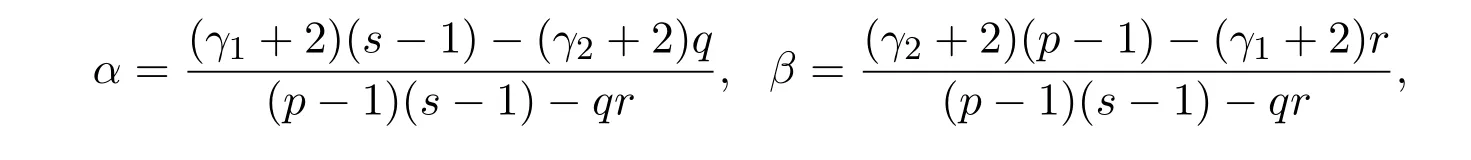
D1,D2,D′1,D′2为正常数.
定理 1.2唯一性:令(u1,v1),(u2,v2)为方程组(1.1)的正解,若
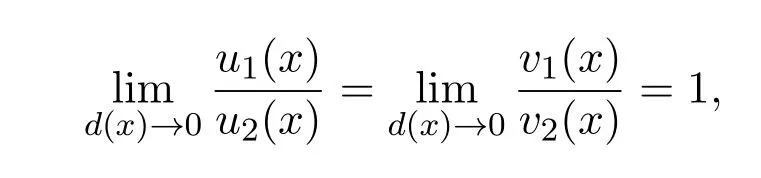
则在Ω中

2 预备知识
考虑下边问题:

其中p>1,γ>-2.由于Ω是C2的,d(x)在∂Ω的邻域上也是C2的,假定d(x)∈C2(¯Ω),方程组(2.1)的解将会在第三部分中用到.首先考虑一般形式:

其中q∈[0,2],g∈C2[0,∞)满足:
(g1)g(0)=0,g在[0+∞)上为增函数;
(g2)对任意的ξ∈(0,1)与所有的s≥0,均有g(ξs)≤ξg(s);

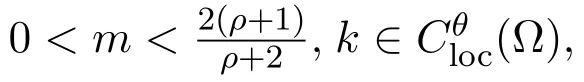

其中
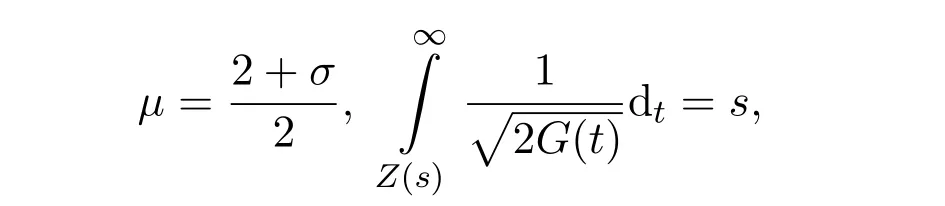
s为任意的正数.
定义2.1定义在[a,∞)(a>0)上的正的可测函数g,称为在无穷远处以指数ρ的正规变换,记为g∈Rρ,若对任意的ε>0与常数ρ∈R 成立,
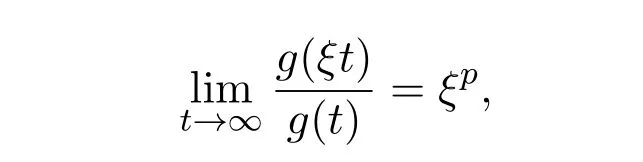
其中ρ为正规变换指数.当ρ=0时,称g在无穷远处缓慢变化,所以若g∈Rρ,则可以写成g(u)=upL(u).

引理2.2[11]表示定理:函数L在无穷远处缓慢变化的充分必要条件是:对某些a>0,存在可测函数c(u),y(s),满足当u→∞时,y(u)→0,c(u)→c(c>0),使得

引理 2.3[12]假设g满足条件(g1)与(g2),则以下条件是等价的.
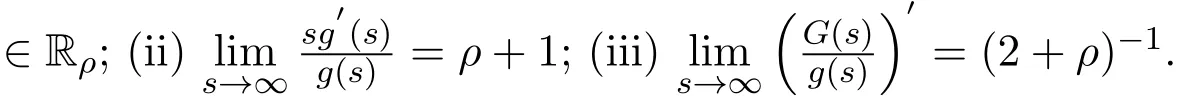

引理 2.4[7]如果g满足(g1)(g2)(g3)且ρ>0,则Z(t)在定理2.1中有下边的性质:



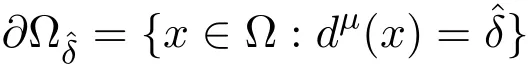
对固定的λ≥0,由∂Ω的正则性,选取ˆδ足够的小,使得
(ii)


由|∇d(x)|=1,得

同理可得
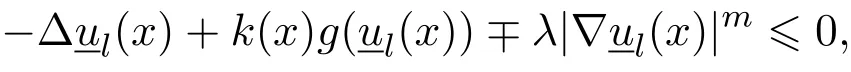
计算过程详见文献[7].

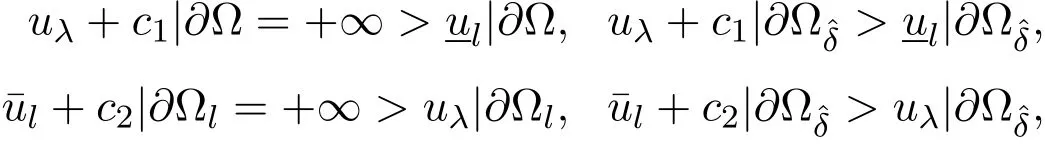
即
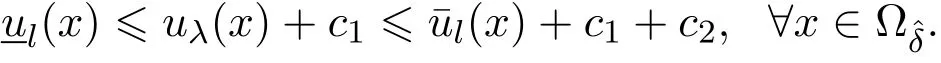
令l→0,得到

即
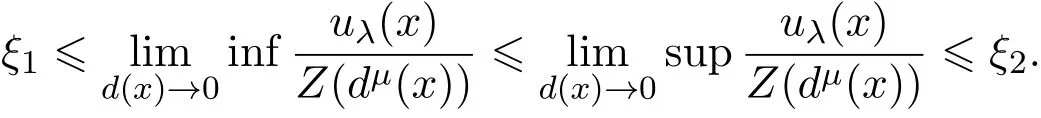
令ξ→0,由ξ1与ξ2的定义,得
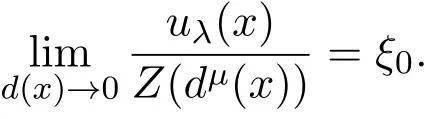
定理得证.
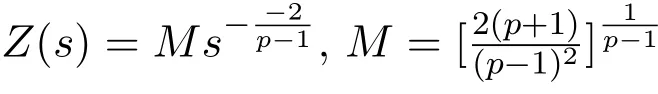
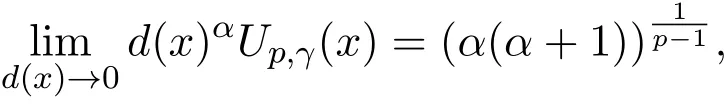
定义2.2首先给出系统


证明记u1为下列方程的唯一的解,



证明取 δ>0,令 Ωδ={x∈Ω,d(x)>δ}且,为定义在 ∂Ωδ上的光滑函数,在∂Ωδ上有≤≤,≤≤.由引理2.5则系统有一个解(uδ,vδ)使得在Ωδ内≤uδ≤,≤vδ≤可知 uδ与 vδ是有界的.存在一个序列 δn→ 0,使得在 Cl2oc(Ω)内 uδn→ u,vδn→ v,其中 (u,v)为方程 (2.3)的解,且在Ω内≤u≤,≥v≥,在∂Ω上u=v=∞.
引理2.7令f,g∈C(¯Ω),u,v∈C2()为方程组∆u+λ|∇u|=f(x),∆v+t|∇v|=g(x) 在 Ω上的解,且在 Ω中 u≤v,其中等号在某些点处取到.假设在 ∂Ω上u<v.则存在x0∈Ω,使得u(x0)=v(x0)且f(x0)≤g(x0).
证明令ζ={x∈Ω:u(x)=v(x)}.由假设可得ζ非空且严格包含于Ω.应用反证法,假设在ζ中f>g.选取ζ的一个开邻域ψ,使得在ψ中f>g,并且在∂ψ上u<v.则对于任意小的ε>0在∂ψ上有u+ε≤v,在ψ中∆u+λ|∇u|=f>g=∆v+t|∇v|.由比较原则得,在ψ中u+ε≤v,这与ζ⊂ψ矛盾.因此,f>g在ζ中不可能成立.所以,存在x0∈ζ,使得f(x0)≤g(x0).
注2
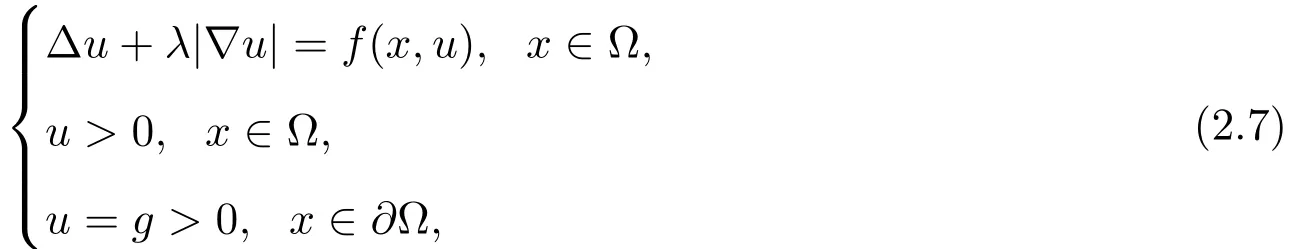
则(2.7)式有唯一的解若函数f(x,u)/u对固定的x关于u是增函数.
引理 2.8假设p,s>1,q,r<0满足(p-1)(s-1)>qr,令(u1,v1),(u2,v2)为下列方程组的正解:

且在∂Ω上f,g>0.则u1=u2,v1=v2.

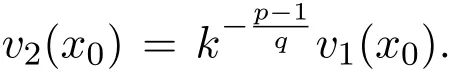


因此

由假设 k>1与 (p-1)(s-1)>qr得 u2(x∗)>ku1(x∗),推出矛盾.这表明 k≤1,并且在Ω中u2≤u1,v2≥v1.相似的,由u2,v2>0在 ¯Ω中,可以证明在Ω中u1≥u2,v1≥v2,引理得证.

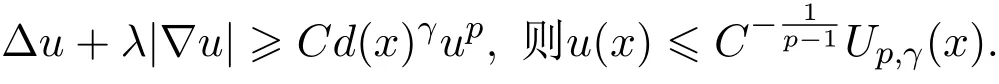

所以

又因为

所以,由比较原则(见文献[12]Theorem 10.1),可得

可以推出


3 定理的证明
定理 1.1的证明(存在性)首先证明(εUp,σ1,ε-δUs,σ2)为方程组(1.1)的一个下解,其
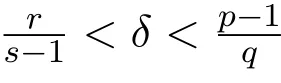
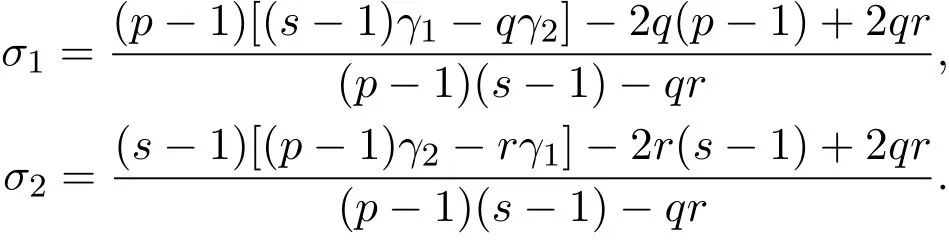


令

由δ的范围,有
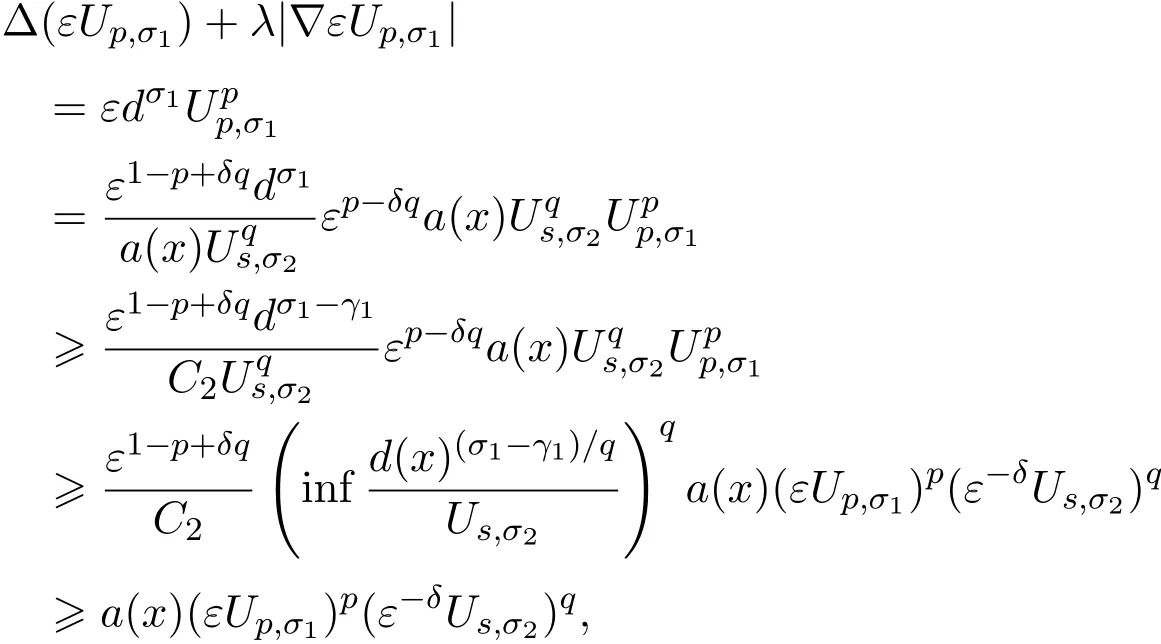
并且
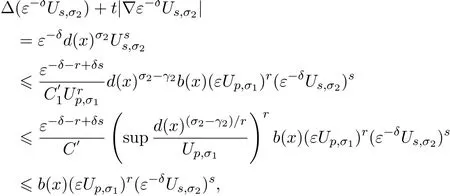
证明了这一需要.
又因为a(x)≥C1d(x)γ1,b(x)≤C′2d(x)γ2,类似的,可证得(MUp,σ1,M-δUs,σ2)为(1.1)式在Ω上的一个上解,其中

由引理2.6得到方程(1.1)存在一组解(u,v).
(爆破速率的估计)令a0=inf v>0,由已知条件v>0,q<0,a(x)≥C1d(x)γ1,可得

由引理2.9可知

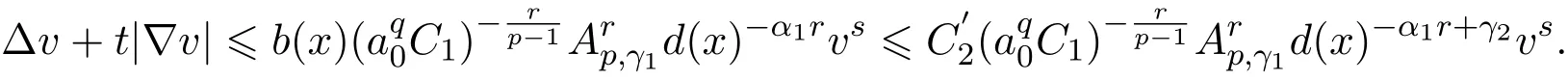
再次应用引理2.9可得
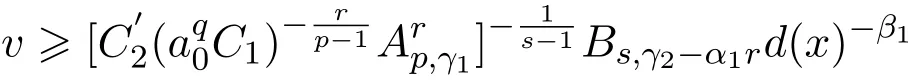

其中

当n→+∞,可以直接计算出


同理,存在D1,D,使得u(x)≥D1d(x)-α,v(x)≥Dd(x)-β.
定理 1.2的证明因为(u1,v1),(u2,v2)为方程组的正解,且

所以,对任意的ε∈(0,1),存在δ>0,使得

在Ωˆρ:={x∈Ω,d(x)≤ˆρ}.设Ωˆρ=Ω¯Ωˆρ,考虑下边的问题
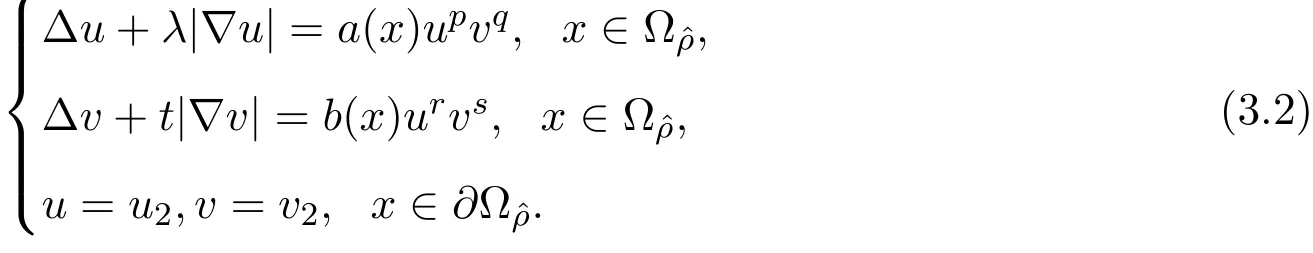
显然,((1-ε)u1,(1-ε)-δv1)与((1+ε)u1,(1+ε)-δv1)为方程组(3.2)的下解与上解,由引理2.6可得在Ωˆρ中至少存在一个解(uˆρ,vˆρ)使得

又由引理 2.8可得 (3.2)的解唯一,即 (u2,v2).所以在 Ωˆρ中 u2=uˆρ,v2=vˆρ.因此,结合(3.1),得
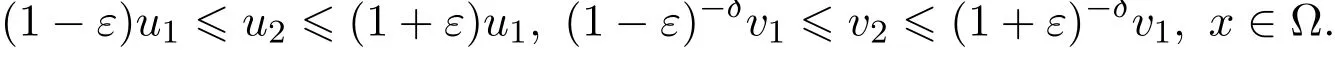
令ε→0,可得在Ω上有u1=u2,v1=v2,则方程组具有唯一解.
[1]Meli´an J G,Rossi J D.Boundary blow-up solutions to elliptic systems of competitive type[J].J.Diff.Eqns.,2004,206:156-181.
[2]Meli´an J G.A remark on uniqueness of large solutions for elliptic systems of competitive type[J].J.Math. Anal.Appl.,2007,331:608-616.
[3]Mu C,Huang S.Large solutions for an elliptic system of competitive type:existence,uniqueness and asymptotic behavior[J].Nonlinear Anal.,2009,71:4544-4552.
[4]Meli´an J G.Large solutions for an elliptic system of quasilinear equations[J].J.Diff.Eqns.,2008,245:3735-3752.
[5]Wang Y,Wang M.Boundary blow-up solutions for a cooperative system of quasilinear equation[J].J.Math. Anal.Appl.,2010,368:736-744.
[6]Bandle C,Giarrusso E.Boundary blow-up for semilinear elliptic equations with nonlinear gradient terms[J]. Adv.Diff.Eqns.,1996,1:133-150.
[7]Zhang Z.The asymptotic behaviour of solutions with boundary blow-up for semilinear elliptic equations with nonlinear gradient terms[J].Nonlinear Anal.,2005,62:1137-1148.
[8]Zhang Z.Boundary blow-up elliptic problems with nonlinear gradient terms[J].J.Diff.Eqns.,2006,228:661-684.
[9]Zhang Z.Boundary blow-up elliptic problems with nonlinear gradient terms and singular weights[J].Proc. Roy.Soc.Edinburgh Sect.A,2008,138:1403-1424.
[10]Chen Y J,Pang Y H,Wang M.Blow-up rates and uniqueness of large solutions for elliptic equations with nonlinear gradient term and singular or degenerate weights[J].manuscripta math.,2013,141:171-193
[11]Seneta E.Regularly Varying Functions[M].New York:Springer-Verlag,1976.
[12]Cˆ1rstea F,Rˇadulescu V D,Uniqueness of the blow-up boundary solution of logistic equations with absorbtion[J].C.R.Acad.Sci.Paris,Ser.I.,2002,335:447-452.
[13]Gilbarg D,Trudinger N S.Elliptic Partial Differential Equations of Second Order[M].3rd ed.Berlin:Springer,1998.
2010 MSC:35J57,35B44
Boundary blow-up solutions for an elliptic system with a gradient term
Li Hua,Ma Feiyao
(Department of Mathematics,Ningbo University,Ningbo315211,China)
The properties of boundary blow-up solutions for an elliptic system with a gradient term are studied,where the weight functionsa(x),b(x)are positive and satisfy certain conditions.By the methodof suband super-solutions and comparison principle,the existence and uniqueness of positive solutions are proved and the estimates of boundary blow-up rate are obtained.
elliptic systems,gradient term,boundary blow-up
O175.25
A
1008-5513(2016)04-0387-12
10.3969/j.issn.1008-5513.2016.04.007
2016-05-31.
国家自然科学基金(11201250).
李华(1989-),硕士生,研究方向:偏微分方程.

