Fell topology,Choquet capacity and capacity-ergodic systems
dedicated to the memory of Yangeng WangLi Rui,Wei Guo,Dooling Tom,Bourquin Steven(.School of Statistics&Mathematics,Shanghai Finance University,Shanghai 009,China;.Department of Mathematics&Computer Science,University of North Carolina at Pembroke,Pembrokeao North Carolina 87,U.S.A. .Department of Chemistry&Physics,University of North Carolina at Pembroke,Pembroke,North Carolina 87,U.S.A.)
Fell topology,Choquet capacity and capacity-ergodic systems
dedicated to the memory of Yangeng Wang
Li Rui1,Wei Guo2,Dooling Tom3,Bourquin Steven2
(1.School of Statistics&Mathematics,Shanghai Finance University,Shanghai 201209,China;2.Department of Mathematics&Computer Science,University of North Carolina at Pembroke,Pembrokeao North Carolina28372,U.S.A. 3.Department of Chemistry&Physics,University of North Carolina at Pembroke,Pembroke,North Carolina28372,U.S.A.)
This paper contains a review of the Fell topology,reinstalls the role of Choquet capacities in probability theory,and generalizes the notion of ergodic measures to the non-additive counterpart of ergodic Choquet capacities.Further,an ergodic capacity system is constructed through a hyperbolic toral automorphism,with relevant dynamical properties explored.
Fell topology,stationary Poisson process,hyperbolic toral automorphism,ergodic Choquet capacity
2010 MSC:60D05,49J45Document Code:AArticle ID:1008-5513(2016)04-0506-16
1 Fell topology
Given a topological space E,let F(E),G(E),and K(E)denote respectively the sets of all closed,open and compact subsets of E,abbreviated as F,G,and K(∅∈F,∅∈G and∅∈K).
The Fell topology τfon F(also known as H-topology[1],hit-or-miss topology[2,3],Choquet-Matheron topology[4],or weak Vietoris topology[5])is generated by the subbase

where FK={F∈F|F∩K=∅}and FG={F∈F|F∩G/=∅}.A topological base of τfis

A sequence{Fn}of closed subsets of E converges to a closed subset F of E in F iff(see Matheron[6])
(i)If an open set G hits F,then G hits all the Fs except at the most a finite number of F′ns.
(ii)If a compact set K is disjoint of F,then it is disjoint of all the Fn’s except at the most a finite number of Fs.
The above criteria(i)and(ii)are respectively equivalent to the following(i)′and(ii)′.
(i)′For every x∈F,there exists for each integer n a point xnin Fn(except,at the most, for a finite number of F)such thatxn=x in E.
(ii)If Fis a subsequence of F,andx(x)is an arbitrary convergent sequence,′nknnknk∈Fnkthenxnkis in F.
The Fell topology τfon arbitrary underlying spaces(Hausdorff or not)was introduced by Fell in 1962 for constructing the regularized dual space of C*-algebra[1,7].In 1975,Matheron re-discovered this topology when investigating the distribution and Choquet Theorem of random sets[6].Earlier investigation of this topology were in fact given by Watson in 1953[8]and Mrowka in 1958[9]who studied the topologies of closed convergence in locally compact separable(LCS)metric spaces and locally compact Hausdorff spaces,respectively.
As a variation of the Vietoris topology,defined as the meet of the co-compact topology and lower Vietoris topology[3,6,10],the Fell topology is closely related to the Vietoris topology,Hausdorff metric,Wijsman topology,and upper Kuratowski topology(a topologization)(see e.g.Matheron[6],Beer[10],Michael[12],and the summary in our paper[13-16]).In particular,the Fell topology and Kuratowski topology coincide(Dolecki,Greco and Lechicki[17],Nogura and Shakhmatov[3],Beer[10]).
In 1964,Flachsmeyer proved,based on Fell′s work and the Urysohn′s metrization theorem (Engelking[18]),that for any Hausdorff space E,the Fell topology is metrizable iff E is locally compact second countable(equivalently,LCS metrizable)(Flachsmeyer[19];see also Beer [10,20]).
For non-Hausdorff underlying spaces,Zsilinszky in 2000 investigated the metrizability of the Fell topology and obtained a necessary and sufficient condition(locally compact,regular and second countable)[21].
So far,four compatible metrics of the Fell topology are known.See 1)Watson[8],Rockafellar and Wets[22,23],Zhou[24],Wei and Wang[25]),2)Lechicki and Levi[26],3)Molchanov [2],Wei and Wang[25],and 4)Wei and Wang[13].Moreover,for the structures of compatible metrics,see Wang,Wei and Li[27].
2 Random closed sets and their Choquet capacities
Random sets theory provides a natural framework for representing in an elegant way the imprecision of the data available to a statistician(see Matheron[6],Molchanov[2],and Nguyen[28]for extensive references).Similar to the idea of using confidence intervals,due to the imperfection of the data acquiring procedures,it may be preferable to represent the outcome of an experiment as a set to which the true value of the measured quantity belongs rather than trying to ascribe to it some unique value(e.g.the center of the uncertainty interval)or a subjectively chosen probability distribution.In such situations it is particularly convenient to model the observation as a random set containing almost surely the random element corresponding to the true result of the experiment(Schreiber[29]).
2.1Choquet capacities as Non-additive set functions
The mathematical objects that govern the probabilistic laws of random closed sets(RACS) are the Choquet capacities,which share some properties of the traditional measures such as continuity from below and monotonicity,but also differ from the traditional measures,e.g.,lack of the additivity over disjoint regions and absence of the continuity from above(equivalent to upper semicontinuity).
In contrast to the traditional measures such as the Lebesgue measure that calculate the quantity of physical extents that are contained in a set,the capacity of a set explores the ability or potential of the set to hold the physical extents subject to a certain given condition.
For example,a capacity may describe the ability of a body to hold an electrical charge or mass for maintaining a specified equilibrium potential.It is known that for any compact set K in a space E such as Rn,there exists a unique admissible measureµdefined on K such that the resulting potential is 1 almost everywhere in K,except at most at points of a set of exterior capacity 0.Thisµis the equilibrium distribution and its potential is the equilibrium potential of K.The equilibrium distribution is the only admissible measure on K whose total charge or mass is equal to the capacity T(K)(see Choquet[30]).The mathematical formulation of this kind of physical phenomena is the Choquet capacity,which in fact holds a strong subadditivity:T(K1∪K2)+T(K1∩K2)≤T(K1)+T(K2).
In the literature,Choquet capacities are often regarded as hitting probabilities,as preciselyillustrated Example.
If a probability function P satisfies the countable additivity,then P is continuous from above(An↓A⇒P(An)↓P(A))and from below(An↑A⇒P(An)↑P(A));conversely,if a function P satisfies P(A)≥0 and P(S)=1,is finitely additive,and is continuous from above (at the empty set∅)or continuous from below,then P is countably additive.
A probability measureµis both continuous from below and above,and it′s(countably) additive.The additivity implies the Subset Property:For anyµ-measurable sets A and B,
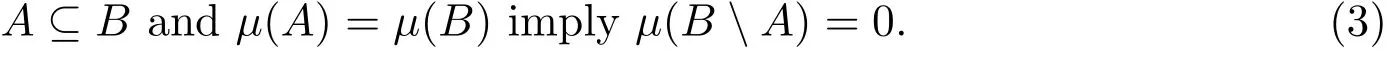
However,while a Choquet capacity T is continuous from below as well as continuous on any decreasing sequence of compact subsets,it is not necessarily continuous from above;for Choquet capacities,continuity from above is equivalent to the upper semicontinuity(see Wei,Wang,Nguyen and Beken[14]).Further,even if T is both continuous from below and from above,and holds a similar subset property:For any T-capacitable sets A and B,
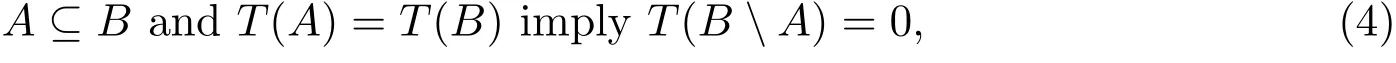
T is still not necessarily additive(Example).
2.2Significance of Choquet capacities
Choquet capacities,introduced by G.Choquet,a pioneer of the theory of non-additive set functions,are non-additive set functions and have influences on many parts of mathematics and different areas of sciences and technology,e.g.decision theory and social choice problems [31-39].Choquet capacities are widely applied to mathematical finance,e.g.cooperative games (Shapley[40]),stochastic dominance and risk measures(Sriboonchitta et al.[41]),uncertainty in economic theory(Marinacci et al.[42]).Specially,on the multi-criteria decision aiming at ordering multidimensional alternatives where the traditional weighted sum that relies on a rarely verified independence of criteria is replaced by a Choquet integral with respect to a capacity(Grabisch[43,44],also refer to Grabisch et al.[35];Marichal[45,46]).This approach was further developed by Kojadinovic(Kojadinovic[47]).
In terms of Choquet capacities,the Choquet integral(see Matheron[6],Molchanov[2]and Nguyen[28])was introduced to generalize the traditional Lebesgue-Stieltjes integral(Lebesgue-Radon integral)where the latter(Lebesgue-Stieltjes integral)requires a regular Borel measure that is associated to functions of bounded variation on the real line(another integral based on monotonic set functions is Sugeno′s integral Sugeno[48]).
Recall that E is a LCS metric space,such as Rnor other manifolds encountered in applications of mathematics.The Choquet integral of a measurable function g:E→R+withrespect to a Choquet capacity T(more general,with respect to a non-decreasing non-additive set function)is defined by

compared to the well-known representation of the expectation of an ordinary non-negative random variable X:

Choquet integral was rediscovered by Schmeidler in the framework of decision under uncertainty,where he was looking for representation theorems in utility theory.Schmeidler first put forward an axiomatic model of choice with non-additive beliefs.In order to axiomatize a decision model more flexible than subjective expected utility,Schmeidler weakened the classical independence axiom requiring it only for comonotonic functions and as a consequence,obtained a representation of preferences by a functional which is linear only on comonotonic functions and is exactly a Choquet integral(Chateauneuf[49],Schmeidler[50,51],Gilboa[52]).
Another role of Choquet capacities in probability theory is the characterization of probability laws of random closed sets(RACS).RACS serve as general mathematical models for set-valued observations and irregular geometrical patterns of physical phenomena,generalize the traditional concept of ordinary random variables,which are regarded as models for point-valued observations,and play an important role in stochastic geometry.RACS have direct applications in the fields mentioned previously.Early applications of RACS in statistics include statisticians designing to understand the basic principles of(finite)population sampling(see Hajek[53]).In parameter estimation,if(Ω,A,Pθ,θ∈Φ)is a statistical model,then a multi-valued mapping S:Ω -→ 2Φsuch that S-1(θ)={ω|θ∈S(ω)}∈A for allθ∈Φ is a confidence region estimator of the true model parameter,with confidence level 1-α=inf{Pθ(ω|θ∈S(ω)),θ∈Φ}(see Hall[54]).
Still another role is a recently explored application to the stochastic partial differential equations(SPDEs),where,due to a random noise in the equation(forcing term or coefficients),the solution of the equation can be regarded as a random function from a probability space to space of functions,i.e.,h:(Ω,A,P)→RnRm.Thus,h(ω)is a function(a sample path)from Rmto Rn,which stands for the(stochastic)solution of a PDE when a noise term ξ(ω)exists in the equation.Such h is referred as a random field in the literature,which is a generalization of stochastic processes(where the index set is a 2 or higher dimensional space).Now,fix a compact subset K of Rm(of positive Lebesgue measure)and a subset of A of Rn(A can be interpreted as the image of K under the solution of the corresponding non-stochastic equation without thenoise term).The interest in this setting is to estimate the following hitting probability:

in terms of the capacity of A or the Hausdorff measure of A.See e.g.Mueller and Tribe [55],Dalang and Sanz-Sol´e[56],Dalang et al.[57-60](Gaussian stochastic waves,Malliavin calculus,non-linear stochastic waves etc).This setting is connected to our research on random upper semicontinuous functions(Nguyen,Wang and Wei[61]).
A recent application demonstrates again the usefulness of RACS to statistics.Recall that the sample quantile is a strongly consistent estimator of the population quantile(Serfling [62],p.75),and the weak consistency of sample quantiles as estimators of population quantiles was shown by Smirnov(Smirnov[63];see also Resnick[64],p.179).Das and Resnick in 2008 applied random set theory to statistics by considering the set Snof points forming the quantilequantile plot as a RACS in R2:Under certain regularity conditions on the given heavy tailed distribution F,Snconverges in probability to a closed,non-random set(Das and Resnick[65]).
In 2010,Martin,Zhang and Liu studied Dempster-Shafer Theory and statistical inference with weak beliefs[66].In 2011,Zhang and Liu proposed a variation of Dempster-Shafer inference([67]).
Most recently,Martin and Liu et al.studied in a series of papers the inferential models(IMs),aiming at not only providing data-dependent probabilistic measures of uncertainty about the unknown parameter,but doing so with an automatic long-run frequency calibration property([68]).They extended the word on the theory of statistical inference with weak beliefs;for obtaining desirable frequency properties,they introduced the concepts of IMs.According to them,Dempster-Shafer inference does not have some of the desired frequency properties.
3 Choquet capacities and Choquet Theorem
Let E be a given LCS metric space with metric d,P the class of all subsets of E,F the hyperspace of all closed subsets of E equipped with the Fell topology,and K the class of all compact subsets of E.
A capacity is a map T:P→[0,1]satisfying following three conditions(Matheron[6]):
(i)If A,B∈P and A⊆B,then T(A)≤T(B);
(ii)For A,An∈P(n∈N),if An↑A in P(i.e.,An⊆An+1for n∈N and∪1An=A),then T(An)↑T(A);
(iii)For K,Kn∈K(n∈N),if Kn↓K in K(i.e.,Kn+1⊆Knfor n∈N and∩1Kn= K),then T(Kn)↓T(K).
A Choquet capacity T requires an additional probability condition,alternating of infinite order which is described as follows.
Let K,K1,K2,...be compact sets of E,and let∆n(K;K1,...,Kn)be the probability for the RACS X to hit K1,...,Knbut miss K.Then all functions∆ndefined below must be non-negative(see Matheron[6]):


and consequently,(7)is equivalent to the following condition:T is monotonically increasing on K and the inequality
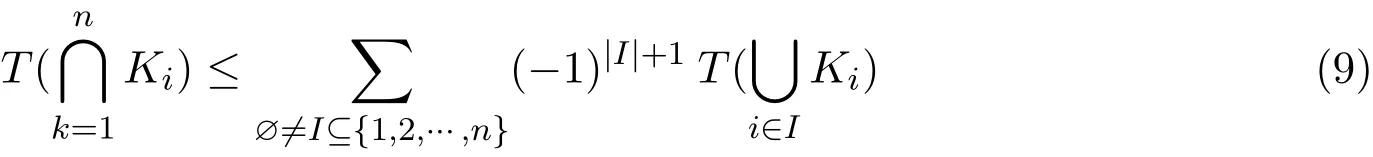
holds for all n≥2(Nguyen[28]).If T is a probability measure,the inequality(9)becomes Poincar´e’s equality(see Nguyen[28]).Moreover,T can be extended to P by first to any open subset G and then to arbitrary subset A of E(see Matheron[6]and Wei et al.[14]).
A RACS X is an A-B(F)measurable function from a probability space(Ω,A,P)to the measurable space(F,B(F)).Regular letter P will represent a probability function,italic P will represent the induced probability measure(P=PX-1),and N will denote the set of all non-negative integers.
The Choquet capacity T of X characterizes the probability law P of X through the Choquet Theorem below.The Choquet Theorem has been extensively investigated in the context of probability,e.g.[2,4-6,13,14,25,28,30,61,69-74].
Choquet Theorem:(see Matheron[6])Let E be a LCS metric space and F the space of all closed sets of E equipped with the Fell topology.Then there exists a(necessarily unique) probability measure P on the Borel σ-field B(F)generated by the topology of F satisfying T(K)=P(X∩K/=∅)=P(FK)for K∈K if and only if T is a Choquet capacity on K with 0≤T≤1 and T(∅)=0.
Choquet Theorem is the foundation of random set theory.It reveals the relationship between the Choquet capacity T of X and the probability measure P of X.In this theorem,the probability law P describes the random evolution of X;the Choquet capacity T plays the role of the distribution functions of ordinary random vectors;the Fell topology governs the convergence of closed sets,which is consistent with the standard convergence of closed sets(see Matheron[6];Wei and Wang[13,14]).The theory of RACS originates from the hit-probability (miss-probability).
In particular,any ordinary random variable taking point values in a metric space E can be viewed as a special RACS,a random singleton set,and hence it is completely characterized by its associated Choquet capacity.See e.g.,Molchanov[2],Wei and Wang[13,14].


4 Invariant and ergodic capacities:constructing an example
For any Choquet capacity T defined on a LCS metric space E,every Borel set B⊆E is capacitable(Meyer[75]),thus

Let CTbe the set of all T-capacitable subsets of E,abbreviated as C,and f:E→E a T-capacitable transformation.
Analogous with the measure-ergodic theory,a research on the invariant and ergodic capacities was conducted(see Wei,Wang and Li[73],2010;Wei,Wang and Yang[74],2011).
The following definition generalizes the concept of ergodic measures to the non-additive setting of Choquet capacities.
Definition 4.1Suppose T is f invariant(or say f preserves T),i.e.,T(f-1(B))=T(B) for B∈C.If for any T-capacitable and f-invariant set B,it holds T(B)=T(E)or T(B)=0,then T is said to be an ergodic Choquet capacity of f(or f is T-ergodic).
We now turn to transformations on the torus,invariant Choquet capacities,and Choquet capacities on the torus.
Hyperbolic toral automorphisms on the torusT2:
Let A=(ai,j)be a m by m matrix with integer entries.A defines a transformation fA:Tm→Tmon the torus as follows:
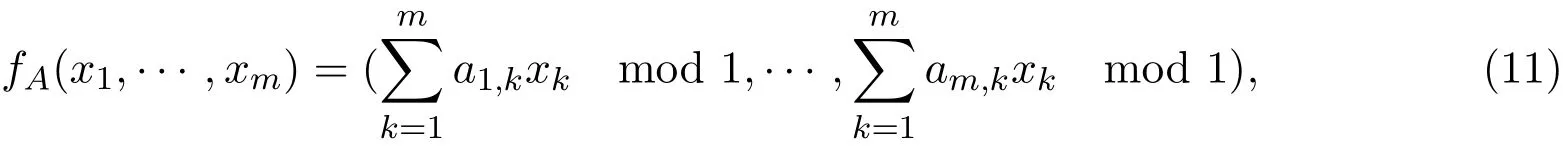
where Tm=S1×...×S1(m times)or which is the same,Tm=Rm/Zm=R/Z×...×R/Z (m times)(recall that a circle is identified with a half-open and half closed interval).
When det(A)=±1,fAis a toral automorphism,and furthermore,if A has no eigenvalues of modulus 1,fAis hyperbolic.We assume that A satisfies these conditions in the following. It is known that fApreserves λ.Actually,all hyperbolic toral automorphisms preserve λ. All hyperbolic toral automorphisms are topologically transitive(but not minimal,since they have dense periodic points)-see Devaney[76]or Aoki and Hiraide[77].
Topological transitivity is a necessary but not sufficient condition for ergodicity of a dynamical system(see Halmos[78],Sidorov[79-82]).
The measure on Tmis the m-dimensional Lebesgue measure λ,normalized to λ(Tm)=1. It is known that fAdefined in(12)preserves λ and is ergodic(Devaney[76],Aoki and Hiraide [77],Halmos[78],Sidorov[79-82],Hasselblatt and Katok[83],Brin and Stuck[84],Walters [85],Pollicott and Yuri[86],Ye et al.[87],Brucks and Bruin[88]).Due to the similarity,we will take the 2-dimensional torus T2=S1×S1as the underlying space.Given a matrix A=()where a,b,c,d∈Z,A determines a mapping from the torus to itself,i.e.,

Particularly,the Arnold’s continuous automorphism of the torus(CAT)is defined by A=(), i.e.,fA(x,y)=(2x+y mod 1,x+y mod 1).
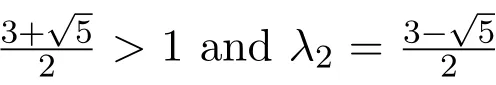
Example 4.1Let{Wt|t≥0}be a stationary Poisson process with intensity rate λ,and(Ω,A,P)the probability space for each of the random variables Wt,t≥0.For t≥0,the expected value of Wtis λt.Also,let α denote the uniform random variable on the torus T2,with(Ω′,A′,P′)the corresponding probability space.
Given t>0,let α1,α2,...,αWtbe a collection of Wtmany uniform random variables on the torus T2,identically distributed and independent each other.Then,we define a random finite set Xt=Xα1,α2,...,αWt,whose probability space(Ω′,A′,P′)is obtained as the product probability space of(Ω,A,P)and(Ω′,A′,P′),by letting Xt(ω,ω′)contain α1(ω′),α2(ω′),...,αWt(ω)(ω′).If Wt(ω)=0,define Xt=∅(thus P(Xt=∅)=P(Wt=0)=e-λt).
Now,for each t> 0,we will determine the Choquet capacity Ttof Xt(strictly,the notation is TXt),i.e.,for any compact subset K of T2,we will calculate the capacity Tt(K),the probability of Xthitting K,as follows:

whereµis the Haar measure on T2(Lebesguq measure up to normalization). By the Choquet Theorem,the probability measure Ptof Xtsatisfies

Properties of the Choquet capacity Tt,t>0:
(i)Ttis both continuous from below and from above,and it possesses the subset property. However,it is non-additive.These properties can be verified using the methods given in[?].
(ii)Ttis fA-invariant,i.e.,fApreserves the capacity Tt.
In fact,it is known that fApreserves the Haar measureµon T2.Now,for any compact subset K of T2,we have Tt(f1(K))=1-e-λµ(f1(K))=1-e-λµ(K)=Tt(K).
Further,for any T-capacitiable subset C of T2,it follows from
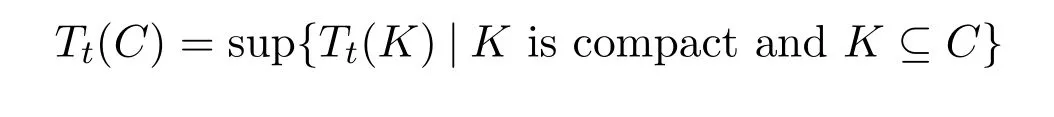
that Tt(f1(C))=Tt(C).
The next property is about the ergodicity of Tt.Clearly,the relation between Ttand µincludes:Tt(K)=0 iffµ(K)=0,andµ(K)=1 iff Tt(K)=1-e-λt(which is due to P(Xt=∅)=P(Wt=0)=e-λt).
Recall Definition:an f-invariant Choquet capacity T is ergodic if any f-invariant capacitiable subset has a capacity 0 or the full capacity(i.e.,the largest possible capacity).
(iii)Ttis ergodic.It is known that fAis measure-ergodic(it is a toral automorphism determined by the matrix A that has no eigenvalues which are roots of unity).
Hence,if K is any compact invariant set of fA,it holds thatµ(K)=1 or 0,and hence Tt(K)=1-e-λµ(K)or 0.Moreover,this property can be extended to any Tt-capacitiable and fA-invariant subset C of T2,again due to Tt(C)=sup{Tt(K)|K is compact and K⊆C}.
(iv)Subsequently,we have generalized the concept of measure-ergodic systems to capacityergodic systems,and constructed such an capacity-ergodic system:(T2,C(T2),Tt,fA).
Ending Note.Non-additive probabilities are increasingly used for modeling irregular physical quantities that are held within sets,e.g.Choquet capacities.Built upon capacities,Choquet integral generalizes the Lebesgue integral to non-additive measures.Early studies on non-additive probabilities can be tracked to Jacob Bernoulli,a 17th century pioneer in the mathematics theory of chance,and Johann Heinrich Lambert,a broad-ranging 18th century scholar(see[89]).
Lebesgue theory and probability theory are proven to be theoretically important and practically useful parts of mathematics.Built upon Choquet capacities,Choquet integral(resp.,random set theory)accommodates non-additive physical quantities(resp.,irregular geometrical patterns,instead of pointwise ones).Therefore,a rigorous and systematic study of capacities through new probability models(capacity systems and ergodic capacity systems)will succeed in accomplishing a deeper understanding of non-additive probabilities,more suitable models for irregular physical phenomena,and significant impacts on the applications of Choquet theory for non-additive physical quantities.
5 Appendix:Relations between Fell topology,Vietoris topology and Hausdorff metric
The Vietoris topology τvon 2E[12](the notation CL(E)is also used,e.g.,[10,90,91]),the family of all non-empty closed subsets of E,is generated by the base[11,12,18]

where U1,U2,...,Unare open subsets of E.Clearly,2E=F{∅}.Alternatively,a subbase of the Vietoris topology on 2Ecan be obtained from(1)by replacing F by 2Eand compact subsets K by closed subsets F.It follows from these definitions that the Vietoris topology is finer than the subspace topology on 2Einduced by the Fell topology.
The Hausdorff metric dH(which induces topology τdH)on the family of all non-empty bounded closed subsets of a metric space(E,d)is defined by[18]

τdHand τvare consistent on the space C of non-empty compact subsets of E[18,90,92,93]. τdH⊆τviff(E,d)is totally bounded;τv⊆τdHiff(E,d)is UC,i.e.,every real-valued continuous function on(E,d)is uniformly continuous[94-96].
When E is a compact Hausdorff space,τfand τvare both compact and consistent on 2E. When E is compact metrizable,τf,τvand τdHare all compact and consistent on 2E[1,6,12];in either of these two cases,∅is an isolated point of F.
Critically,when E is LCS metrizable,τfon F is always compact metrizable,and again LCS metrizable on 2E[6],implying that τfon F is metrizable and any consistent metric is complete,separable and totally bounded by the Urysohn’s metrization theorem[18].
In contrast,if E is non-compact such as Rn,τvis neither metrizable nor compact[10,12]. Moreover,the use of Hausdorff metric dHon K faces a difficulty in characterizing the topological structure induced by the Hausdorff metric dH:the topology τdHinduced by dHdepends on the metric d,i.e.,τdHis not metric independent,but metric dependent(Naimpally[94-96]).
More advantages of the Fell topology were extensively explored through the studies of RACS,see e.g.,Matheron[6],Molchanov[2],Wei and Wang[13,14,61],and hyperspace dynamics,see e.g.Wang and Wei[15,16,97].An example illustrating the differences in convergence between these hyperspace topologies was given in our paper[16].
For the Vietoris topology and Hausdorff metric,we refer to Wei,Wang,Nguyen and Beken [14]and Wei,Wang and Yang[74].The relation between these hyperspace topologies is given by Watson[8],Rockafellar and Wets[22,23],Wei and Wang[25]),Naimpally[94-96].The construction of Borel σ-algebra on the hyperspace equipped with the Fell topology was given by Matheron[6].
Thebibliography
[1]Fell J M G.A Hausdorff topology for the closed subsets of a locally compact non-Hausdorff space[J].Proc. Amer.Math.Soc.,1962,13:472-476.
[2]Molchanov I.Theory of Random Sets[M].London:Springer-Verlag,2005.
[3]Nogura T,Shakhmatov D.When does the Fell topology on a hyperspace of closed sets coincide with meet of the upper Kuratowski and the lower Vietoris topology[J].Top.Appl.,1996,70:213-243.
[4]Stoyan D.Models and statistics[J].Interna.Stat.Review,1998,66:1-27.
[5]Wei G.Contributions to Distributions of Random Sets on Polish Spaces,PhD Thesis[M].New Mexico:New MexicoState University,Las Cruces,1999.
[6]Matheron G.Random Sets and Integral Geometry[M].New York:John Wiley&Sons,1975.
[7]Fell J M G.The structure of algebras of operator fields[J].Acta Math.,1961,106:233-280.
[8]Watson P D.On the limits of sequences of sets[J].Quart.Jour.Math.,1953,4(2):1-3.
[9]Mrowka S.On the convergence of nets of sets[J].Fund.Math.,1958,45:237-246.
[10]Beer G.Topologies on Closed and Closed Convex Sets[M].Dordrecht:Kluwer Acad MIA 268,1993
[11]Vietoris L.Bereiche zweiter ordnuang[J].Monatshefte f¨ur Mathematik und Physik,1923,33:49-62.
[12]Michael E.Topologies on spaces of subsets[J].Trans.Amer.Math.Soc.,1951,71:152-182.
[13]Wei G,Wang Y.Formulating stochastic convergence of random closed sets on locally compact separable metrizable spaces using metrics of the hit-or-miss topology[J].Interna.J.Intelligent Tech.Appl.Stat.,2008,1:33-57.
[14]Wei G,Wang Y,Nguyen H T,et al.On the upper semi-continuity of Choquet capacities[J].Interna.J. Approx.Reason,2010,51:429-440.
[15]Wang Y,Wei G,Campbell W H.Sensitive dependence on initial conditions between dynamical systems and their induced hyperspace dynamical systems[J].Top.Appl.,2009,156:803-811.
[16]Wang Y,Wei G,Campbell W H,Bourquin S.A framework of induced hyperspace dynamical systems equipped with the hit-or-miss topology[J].Chaos,Solitons and Fractals,2009,41:1708-1717.
[17]Dolecki S,Greco G H,Lechicki A.When do the upper Kuratowski topology(homeomorphically,Scott topology)and the co-compact topology coincide?[J].Trans.Amer.Math.Soc.,1995,347(8):2869-2884.
[18]Engelking R.General Topology,PWN-Polish[M].Warszawa:Scientific Publishers,1977.
[17]Flachsmeyer J.Verschiedene topologisierungen im raum der abgeschlossenen teilmengen[J].Math.Nachr.,1964,26:321-337.
[19]Beer G.On the Fell topology[J].Set-Valued Anal.,1993,1:69-80.
[20]Zsilinszky L.Note on hit-and-miss topologies[J].Rend.Circ.Mat.Palermo,2000,49:371-380.
[21]Rockafellar R T,Wets R J B.Variational Systems,An Introduction in:A.Dold,B.Eckmann(eds.),Lecture Notes in Mathematics,1091[M].New York:Springer-Verlag,1984.
[22]Rockafellar R T,Wets R J B.Variational analysis,Grundlehren der Mathematischen Wissenschaften[M]. Berlin:Springer-Verlag,1998.
[23]Zhou X.A natural metric on the space of all closed subsets of Rn[J].J.of Shantou University Natural Science Edition,2001,16:62-67.
[24]Wei G,Wang Y.On metrization of the hit-or-miss topology using Alexandroff compactification[J].Interna. J.Approx.Reason.,2007,46:47-64.
[25]Lechicki A,Levi S.Wijsman convergence in the hyperspace of a metric space[J].Bull.Un.Mat.Ital.,1987,7(1-B):439-452.
[26]Wang Y,Wei G,Li R.On metrics of the hit-or-miss topology:direct extensions[J].Pure and Appl.Math.,2008,24:643-645.
[24]Nguyen H T.An Introduction to Random Sets[M].New York:Chapman and Hall,2006.
[25]Schreiber T.Statistical inference from set-valued observations[J].Probability and Mathematical Statistics,2000,20:223-235.
[27]Choquet G.Theory of capacities[J].Ann.Inst.Fourier.,1953-54,5:131-295.
[28]Aumann R J,Shapley L S.Values of Non-Atomic Games[M].New Jersey:Princeton Univ.Press,1974.
[29]Denneberg D.Non-Additive Measure and Integral[M].New York:Kluwer Acad.Publ.,1994.
[30]Dobrakov I.On Submeasures I[M].New Jersey:Diss.Math.,1974.
[31]Falconer K.Fractal Geometry[M].New York:John Wiley and Sons,1990.
[32]Grabisch M,Nguyen H T,Walker E A.Fundamentals of Uncertainity Calculi with Application to Fuzzy Inference[M].New York:Kluwer Acad.Publ.,1995.
[33]Huber P J.The use of Choquet capacities in statistics[J].Bull.Int.Inst.Statist.,1973,45:181-191.
[34]Pap E.Null-Additive Set Functions[M].New York:Kluwer Acad.Publ.Ister.,1995.
[35]Sugeno M,Murofushi T.Pseudo-additive measures and integrals[J].J.Math.Anal.Appl.,1987,122:197-222.
[36]Wang Z,Klir G.Fuzzy Measure Theory[M].New York:Plenum Press,1992.
[37]Shapley L S.A Value for N-Person Games,in Contributions to the Theory of Games[M].New Jersey:Princeton University Press,1953.
[38]Sriboonchitta S,Wong W-K,Sompong D,et al.Stochastic Dominance and Applications to Finance,Risk and Economics[M].Florida:Chapman and Hall/CRC Press,2009.
[39]Marinacci M,Montrucchio L.Introduction to the mathematics of ambiguity,in:I.Gilboa(ed.),Uncertainty in Economic Theory[M].New York:Routledge,2004.
[40]Grabisch M.Fuzzy integral in multicriteria decision making[J].Fuzzy sets and Systems,1995,69:279-298.
[41]Grabisch M.The application of fuzzy integrals in multicriteria decision making[J].European Journal of Operational Research,1996,89:445-456.
[42]Marichal J L.Aggregation operators for multicriteria decision aid[D].Aggregation operators for multicriteria decision aid[D].Belgium:Institute of Mathematics,University of Li`ege,Li`ege,1998.
[43]Marichal J L.On an axiomatization of the quasi-arithmetic mean values without the symmetry axiom[J]. Aequationes Mathematicae,2000,59:74-83.
[44]Kojadinovic I.An axiomatic approach to the measurment of the amount of interaction among criteria or players[J].Fuzzy Sets and Systems,2005,152:417-435.
[45]Sugeno M.Theory of fuzzy integral and its applications[D].Japan:Tokyo Institute of Technology,1974.
[46]Chateauneuf A,Cohen M,Denneberg D.General introduction to this special issue on Choquet integral and applications[J].Stat.Papers,2002,43:1-3.
[47]Schmeidler D.Integral representation without additivity[J].Proc.Amer.Math.Soc.,1986,97:255-261.
[48]Schmeidler D.Subjective probability and expected utility without additivity[J].Econometrica,1989,57:571-587.
[49]Gilboa I,Schmeidler D.Maxmin expected utility with non-unique prior[J].J.Math.Economics,1989,18:141-153.
[50]H´ajek J.Sampling from A Finite Population[M].New York:Marcel Dekker,1981.
[51]Hall P.Introduction to the theory of coverage processes[M].New York:John Wiley and Sons,1988.
[52]Mueller C,Tribe R.Hitting properties of the random string[J].Electron.J.Probab.,2002,7:1-29.
[53]Dalang R C,Sanz-Sol´e M.Criteria for hitting probabilities with applications to systems of stochastic wave equations[J].Bernoulli,2010,16(4):1343-1368.
[54]Dalang R C,Khoshnevisan D,Nualart E.probabilities for systems of nonlinear stochastic heat equations with additive noise[J].ALEA Lat.Am.J.Probab.Math.Stat.,2007,3:231-271.
[55]Dalang R C,Khoshnevisan D,Nualart E.Hitting probabilities for systems of nonlinear stochastic heat equations with multiplicative noise[J].Probab.Theory Related Fields,2009,144:371-427.
[56]Dalang R C,Mueller C,Zambotti L.Hitting probabilities of s.p.d.e.’s with reflection[J].Ann.Probab.,2006,34:1423-1450.
[57]Dalang R C,Nualart E.Potential theory for hyperbolic SPDEs[J].Ann.Probab.,2004,32:2099-2148.
[58]Nguyen H T,Wang Y,Wei G.On Choquet theorem for random upper semicontinuous functions[J].Interna. J.Approx.Reason.,2007,46:3-16.
[59]Serfling R J.Approximation Theorems of Mathematical Statistics[M].New York:John Wiley&Sons,1980.
[60]Smirnov N V.Limit distributions for the terms of a variational series[J].Trudy Mat.Inst.Steklov.,1949,25:3-60.
[61]Resnick S I.A Probability Path[M].Boston:Birkh¨auser,1999.
[62]Das B,Resnick S I.QQ Plots Random sets and data from a Heavy tailed distribution[J].Stochastic Models,2008,24:103-132.
[63]Martin R,Zhang J,Liu C.Dempster-Shafer Theory and statistical inference with weak beliefs[J].Statistical Science,2010,25:72-87.
[64]Zhang J,Liu C.Dempster-Shafer inference with weak beliefs[J].Statistica Sinica,2011,21:475-494.
[65]Martin R,Liu C.Inferential models:Reasoning with uncertainty,Monographs in Statistics and Applied Probability Series[M].Chapman:CRC Press,2015.
[66]Molchanov I.Limit Theorems for Unions of Random Closed Sets,Lecture Notes in Mathematics 1561[M]. New york:Springer-Verlag,1997.
[67]Molchanov I.A generalization of the Choquet theorem for random sets with a given class of realizations[J]. Theory of Probab.and Math.Statist.,1984,28:99-106.
[68]Nguyen H T,Ogura Y,Tasena S,et al.A Note on Random upper Semicontinuous Functions,in:Soft Methods for Integrated Uncertainty Modeling[M].New york:Springer-Verlag,2006.
[69]Stoyan D,Kendall W S,Mecke J.Stochastic Geometry and its Applications[M].2nd ed.Chichester:John Wiley&Sons,1995.
[70]Wei G,Wang Y,Li R.On the relations between ergodic Choquet capacity systems and ergodic hyperspace dynamical systems[J].J.of Northwest University(Natural Science Edition),2010,40:377-378.
[71]Wei G,Wang Y,Yang Z.Methods for constructing Choquet-capacity preserving and ergodic systems:examples[J].Interna.J.Intelligent Tech.Appl.Stat.,2011,4:201-220.
[72]Meyer P A.Probabiliti´es et Potentiel[M].Paris:Hermann,1966.
[73]Devaney R L.An Introduction to Chaotic Dynamical Systems[M].2nd ed.New York:Addison-Wesley,1989.
[74]Aoki N,Hiraide K.Topological Theory of Dynamical Systems,Recent Advances,North-Holland Mathematical Library 52[M].Amsterdam:Elsevier Science B.V.,1994.
[75]Halmos P R.Lectures on Ergodic Theory[M].Tokyo:the Mathematical Society of Japan,1956.
[76]Sidorov Ye A.Connection between topological transitivity and ergodicity[J].Izv.vysh.utcheb.zav.,Mat.,1969,83(4):77-82.
[77]Sidorov Ye A.The existence of topologically indecomposable transformations in an n-dimensional region which are not ergodic[J].Mat.Zametki,1968,3(4):427-430.
[78]Sidorov Ye A.Topologically indecomposable transformations of the n-dimensional space[J].Volzh.Mat. sbornik,1966,5:326-330.
[79]Sidorov Ye A.Smooth topologocally transitive dynamical systems[J].Mat.Zametki,1968,4:441-452.
[80]Hasselblatt B,Katok A.A First Course in Dynamics with A Panorama of Recent Developments[M]. Cambridge,UK:Cambridge University Press,2003.
[81]Brin M,Stuck G.Introduction to Dynamical Systems[M].Cambridge,UK:Cambridge University Press,2002.
[82]Walters P.An Introduction to Ergodic Theory[M].New york:Springer,1982.
[83]Pollicott M,Yuri M.Dynamical Systems and Ergodic Theorem[M].Cambridge,UK:Cambridge University Press,1998.
[84]Ye X,Huang W,Shao S.Topological Dynamical Systems[M].Beijing:Science Press,2008.
[85]Brucks K M,Bruin H.Topics from One-Dimensional Dynamics[M].Cambridge,UK:Cambridge University Press,2004.
[86]Shafer G.Non-additive probabilities in the work of Bernoulli and Lambert[J].Archive for History of Exact Sciences,1978,19:309-370.
[87]Illanes A,Nadler S B.Jr.Hyperspace:Fundamentals and Recent Advances[M].New York:Marcel Dekker Inc.,1999.
[88]Nadler Jr S B.Hyperspaces of Sets.Monographs Textbooks Pure Appl.Math.,vol.49[M].New York:Marcel Dekker,1978.
[89]Peris A.Set-valued discrete chaos[J].Chaos,Solitons&Fractals,2005,26:19-23.
[90]Banks J.Chaos for induced hyperspace maps[J].Chaos,Solitons&Fractals,2005,25:681-685.
[91]Naimpally S A.Comparison of topologies on hyperspaces[J].Annals New York Acad.Sci.,1993,704:273-278.
[92]Naimpally S A.All hypertopologies are hit-or-miss[J].Appl.Gen.Topol.,2002,3:45-53.
[93]Naimpally S A.What is a hit-or-miss topology?[J].Topological Commentary,2003,1:1-3.
[94]Wang Y,Wei G.Characterizing mixing,weak mixing and transitivity of induced hyperspace dynamical systems[J].Top.Appl.,2007,155:56-68.
10.3969/j.issn.1008-5513.2016.04.010
2016-06-13.
Partially supported by HRSA,US DHHS(H49MC00068).作者简介:李瑞(1957-),副教授,研究方向:点集拓扑及其应用.
Fell拓扑,Choquet容量和遍历的Choquet容量系统
李瑞1,卫国2,托马斯·杜林3,史蒂文·布尔坎2
(1.上海金融学院统计与数学学院,上海,201209 2.北卡罗莱纳大学彭布罗克分校化学与物理系,北卡罗莱纳,彭布罗克,28372 3.北卡罗莱纳大学彭布罗克分校数学与计算机科学系,北卡罗莱纳,彭布罗克,28372))
本文描述了Fell拓扑的结构与收敛条件,重新确立了关于随机集的Choquet定理在概率论中的重要作用,并提出了不变Choquet容量的概念.此外,利用环面上的双曲自同构和随机映射,具体构造了一个遍历的Choquet容量系统,且进一步探讨了这种系统的动力性态.
Fell拓扑;稳定Poisson过程;双曲的环面自同构;遍历的Choquet容量
O189

