基于分数阶导数的黏弹性悬架减振模型及其数值方法

李占龙， 孙大刚， 宋　勇， 刘付喜， 赵树萍

(1.西安理工大学 机械与精密仪器学院，西安　710028; 2.太原科技大学 机械工程学院，太原　030024)



基于分数阶导数的黏弹性悬架减振模型及其数值方法

李占龙1,2， 孙大刚1,2， 宋勇2， 刘付喜1， 赵树萍2

(1.西安理工大学 机械与精密仪器学院，西安710028; 2.太原科技大学 机械工程学院，太原030024)

为了准确掌握黏弹性悬架的动态响应，针对传统整数阶减振模型的不足，引入分数阶导数原理，构建了黏弹性材料FKV本构模型，建立了考虑几何参数的黏弹性悬架分数阶减振模型，利用Grumwald-Letnikov定义将模型中分数阶导数离散化，并转化为状态方程形式，依据矩阵函数理论推导出模型的数值解。以某型安装黏弹性悬架的履带车辆参数为例，分别建立了悬架的动态接触有限元模型和分数阶减振模型，获得了在翻越障碍工况下两种模型响应的对比解。结果表明：分数阶减振模型体现了黏弹性悬架响应具有全局相关性和记忆性，且历史作用渐近加强；黏弹性悬架有较好的缓冲减振性能；分数阶减振模型解与有限元方法计算结果有较好的一致性。旨为下一步的实车试验和实际应用提供理论参考。

分数阶导数;黏弹性悬架;减振模型;数值方法

黏弹性悬架(VEDS)为大型履带车辆行走机构的缓冲减振装置，可有效衰减履带车辆在非路面的行走和作业时所产生的大幅动载，增加车辆的附着性能和舒适性能[1]。在复杂随机大载荷作用下，该悬架的黏弹性件内部大分子链反复张弛和互相摩擦而产生热耗，实现对振动能的耗散，达到减振缓冲的目的。

目前对黏弹性悬架的建模分析主要将黏弹性结构简化为无结构特性的流变模型(例如，Maxwell、 Kelvin-Voigt，等)，结合传统动力学方法进行建模计算，或在此基础上增加非线性扰动因子，对阻尼缓冲结构在低频重载大变形条件下的非线性动态响应进行分析[2-4]。上述方法均采用基于局部极限定义的整数阶导数对黏弹阻尼进行描述，对黏弹性材料的历史依赖性和记忆性刻画较差，在较宽频域和较长响应时间内误差尤为明显[5]，所需参数较多，计算过程复杂；另外，描述黏弹性材料力学特性的流变模型是唯象的纯力学简化模型，不包含黏弹性件的几何结构参数，无法讨论其几何参数的影响规律。

分数阶微积分由于其全局相关性能较好地体现系统函数发展的历史依赖过程，在描述复杂物理问题时，与传统整数阶导数模型相比，所需参数较少，且参数物理意义清晰，已被广泛应用于具有长程记忆的演化过程建模(如黏弹性材料本构模型、生物物理、图像处理和随机游走模型等)[6-7]。用分数阶微积分对黏弹性阻尼材料的动力学行为进行描述，即其阻尼力(应力)正比于位移(应变)的分数阶导数(用分数阶算子代替传统整数阶算子)，已被验证对试验数据有很好的拟合性[8-9]。目前，分数阶微积分理论的应用研究主要集中在对黏弹性材料本构模型的建立，从而导出黏弹性材料的分数阶蠕变和松弛形式10-11]；将振动方程中一阶导数阻尼项用分数阶导数代替，获得线性或非线性分数阶振动方程，研究其解析解法和数值算法[12-14]。鲜有将分数阶微积分理论推广到机械工程领域黏弹性缓冲减振结构的动特性分析。

本文构建了分数阶Kelvin-Voigt黏弹性材料本构模型，结合动力学和运动学方程，建立了考虑几何参数的黏弹性悬架减振模型，并将其推演到状态空间，利用Grumwald-Letnikov定义将模型中分数阶导数离散化，依据矩阵函数理论推导出减振模型的数值解，最后以动态接触有限元模型对理论模型数值方法进行了验证。

1　模型建立

1.1黏弹性悬架物理模型

黏弹性悬架安装在履带式车辆的行走机构中(见图1(a))，由钢板和黏弹性件粘结而成，呈上下对称布置(见图1(b))，顶部和台车架相联，底部和对应支重轮的中间筋相联。履带车辆在“非路面”上行驶作业时，悬架会受到冲击型大载荷，并作用在缓冲装置上，使阻尼材料产生形变，由于阻尼材料的迟滞特性，将振动能转化为阻尼材料内部热并逸散，从而降低由悬架传递到车体的冲击振动，提升车辆的稳定性和舒适性以及作业效率。

(a) 实物图　　　　　　　(b) 结构图图1　履带车辆黏弹性悬架Fig.1 VEDS for crawler vehicle

履带式车辆通常需要安装多组黏弹性悬架以获得较好的减振效果和缓减单悬架的受载情况。本文以1/N(N为悬架数)悬架为研究对象。

1.2分数阶减振模型

1.2.1FKV本构模型

选用分数阶Kelvin-Voigt(简称FKV)模型来表征黏弹性材料的力学本构。FKV模型由理想胡克弹簧k和分数阶阻尼元，其中：σe，εe为弹性元应力、应变；σf，εf为分数阶阻尼元应力、应变；σ，ε为FKV模型阻尼应力、应变;k为刚度系数，N/m;c为阻尼系数，N/(m/s);a为分数阶数。分数阶阻尼元描述的阻尼特性介于弹性元件(零阶导数)和理想牛顿流体(一阶导数)，即：

(1)

(2)

式中：f(t)为求导函数，t为自变量，Γ为gamma函数，α为分数阶数，τ为中间变量。

由于并联结构，FKV模型总应变与弹性元和分数阶阻尼元应变相等，即：ε=εe=εf，总应力为弹性元和分数阶阻尼元应力之和，即：σ=σe+σf。故KFV模型本构方程为：

(3)

图2　FKV模型Fig.2 FKV model

1.2.2减振模型

由于黏弹性悬架结构复杂，参数较多，因此在建立减振模型前应对其进行力学简化，为此作如下假设：

①黏弹性部分在悬架行程中上半部分和下半部分接触面积A保持常数； ②履带车辆常在“非路面”行驶或作业时，工作环境温度和路面级别保持稳定，不考虑黏弹性材料的温频效应； ③黏弹性材料变形尚在线性黏弹性范畴，即分数阶数不具有时间依赖性。

基于上述基本假设，将悬架和车体的质量分别等效为m1,m2，单位kg；悬架黏弹性部分用FKV模型代替；悬架、车体质心的绝对位移和地面激励分别为x1,x2和x0，单位m;ke为等效地面刚度，单位N/m。见图3。

图3　黏弹性悬架受力图Fig.3 Force diagram of VEDS

建立黏弹性悬架的减振模型：

1) 动力学方程：

(4)

2) 运动学关系：

(5)

3) 黏弹性材料的广义本构方程：

Pσ=Qε

(6)

式中：Fd为黏弹性元的阻尼力，l为悬架黏弹性件厚度，P,Q是本构微分算子，表达式为：

(7)

(8)

将本构方程和运动学关系代入动力学方程得黏弹性悬架分数阶减振模型：

(9)

化简得：

将分数阶微分算子参数代入式(10)得：

(11)

2　数值求解

将式(11)推演到状态空间：

(12)

(13)

由于

(14)

(15)

对式(15)取截断部分，有：

h-αy(t)+GL(t)

(16)

将式(17)中k个(-1)均摊到分子每一项得：

(18)

因为

Γ(-α)=

(19)

式(18)变化为：

(20)

由于Γ函数性质

Γ(z)=zΓ(z-1)

(21)

式(20)变换为：

(22)

(23)

此时，称bk为历史相关系数，其迭代形式为式(23)，初始条件b0=1。

由式(23)及图4可以看出黏弹性悬架分数阶减振模型具有长程相关性，即历史响应会作用于瞬时响应，且作用渐近加强，类似于整数阶模型的Boltzmann叠加原理，体现了黏弹性材料的历史依赖和记忆特性。

图4　历史相关系数Fig.4 History correlation coefficient

将bk代入GL(t)可得如下迭代公式：

(24)

(25)

依据矩阵理论，式(25)解的形式为：

(26)

将式(26)积分区间替换为[tn,tn+1]，上式离散化为：

(27)

将式(27)等号右端第二项积分采取Simpson离散化，得式(12)的数值解为：

(28)

其中：

Y1(tn)=B1GL(tn+1)+B2p(tn+1)+

因此，结合式(24)、(28)以及初始条件，可利用迭代算法求解黏弹性悬架的动态响应，计算流程如图5。

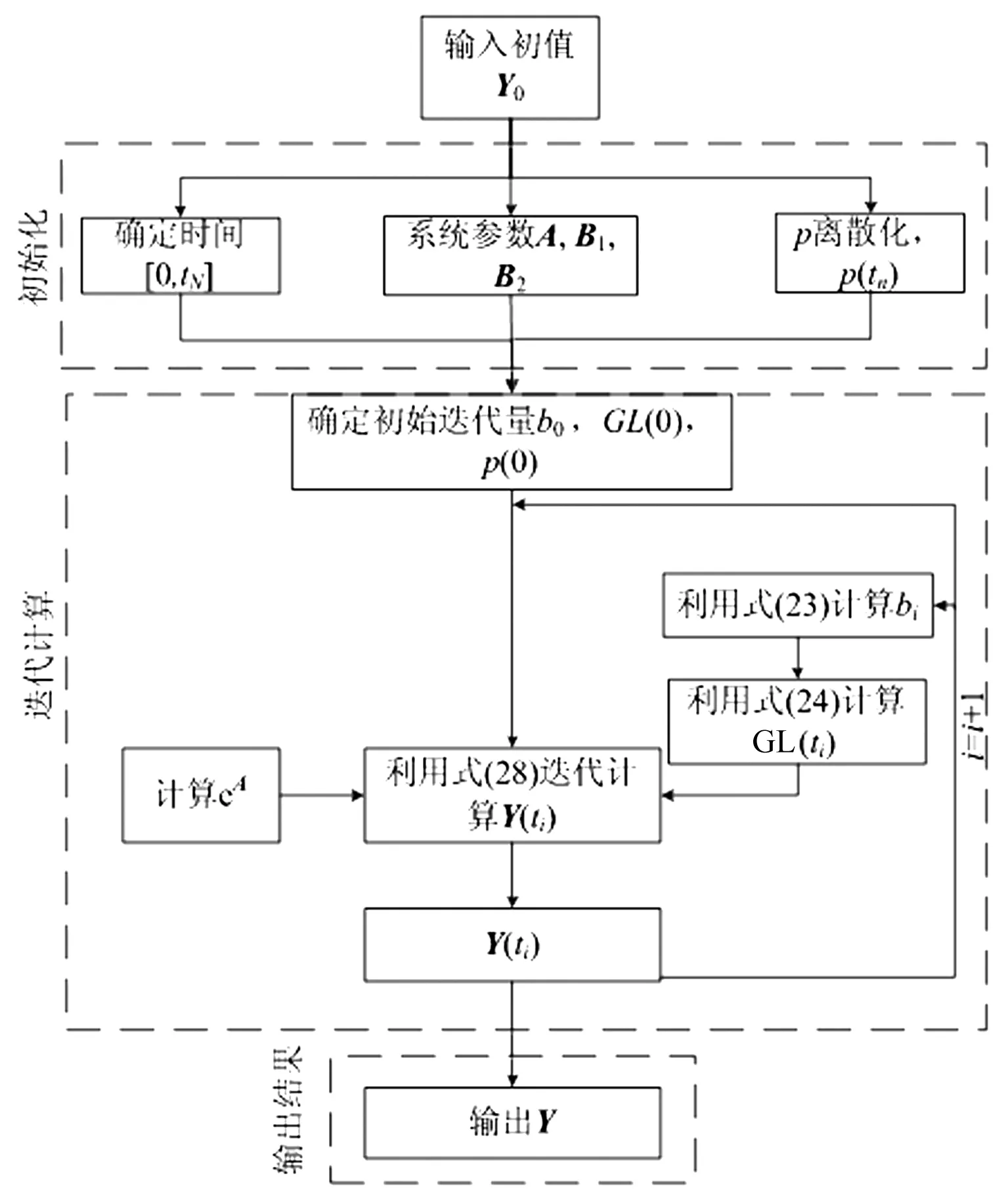
图5　理论模型数值计算流程Fig.5 Flow chart for numerical calculation of VEDS

3　数值方法对比计算

以某履带车辆安装的黏弹性悬架为例，分别建立其动态接触有限元模型和分数阶振动模型，对两种数值方法进行对比计算。

3.1有限元模型

该履带车辆整备质量(带松土器)51 000 kg，整机尺寸为9 630 mm ×4 320 mm ×4 320 mm (长×宽×高)，装配8组该型悬架。悬架黏弹性件为半椭球状(如图6)，其主要结构参数有：底面直径D、顶部圆弧半径R、总高度Ht、顶部圆弧高度Ha、中部高度Hb、底部高度Hc和侧面形状角φ，见表1。

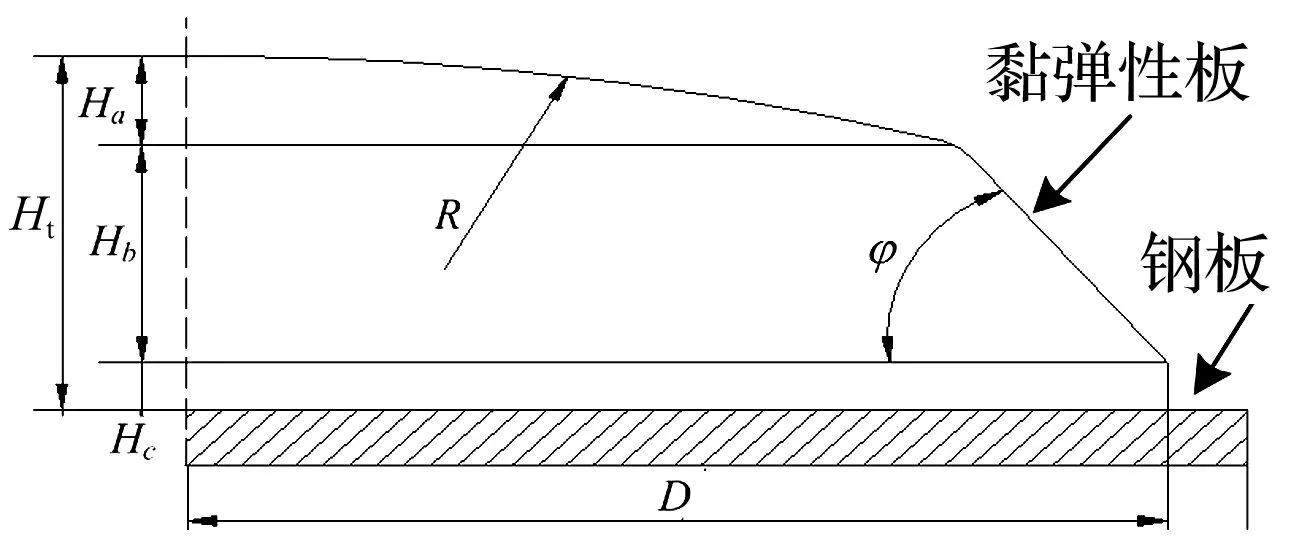
图6　黏弹性件结构Fig.6 Structure of viscoelastic part

参数数值总高度Ht/mm45底面直径D/mm305顶部圆弧半径R/mm950顶部高度Ha/mm10.36中部高度Hb/mm30.6底部高度Hc/mm4.05侧面形状角φ/(°)55

选取悬架的1/4结构，在轴对称截面处施加轴对称约束，最后以实体问题求解。选用Solid 185固体单元和Hyper 58橡胶类单元分别对钢板和黏弹性件网格化；对与黏弹性件固结的上钢板X、Z方向施加约束，对与黏弹性件固结的下钢板采取X、Y方向的耦合，在轴对称截面处施加轴对称约束；对与黏弹性件固结钢板部分，在网格划分时采取共节点；由于地面随机冲击载荷通过支重轮中间筋传递到下钢板上，为了与理论模型简化一致，将此视为均布载荷，施加在下钢板，且利用斜坡分步加载及阶跃平稳加载模拟黏弹性悬架受车辆自重后的动态过程。选用修正的2参数Mooney-Rivlin黏弹性材料应变能密度函数，其特征参数[16]：C01=0.025 MPa，C01=1.246 5 MPa，泊松比ν=0.499，密度1 130 kg/m3；钢板弹性模量E=2.1×105MPa，泊松比μ=0.3，密度7 850 kg/m3。

履带车辆在“非路面”行驶或作业，黏弹性悬架中的黏弹性件受到来自地面和作业对象的低频重载冲击型随机载荷，致使上下黏弹性件的接触分离时而发生，产生动态接触问题。采用罚函数法和拉格朗日乘子混合法来解决黏弹性接触问题，即在黏弹性件接触受压时采用拉格朗日乘子法，分离时采用罚函数法。

3.2分数阶减振模型

计算参数为：m1=550 kg,m2=6 250 kg;ke=6.0×106N/m，k=2.67×107N/m,c=2.13×104N/(m/s),α=0.49，r=152.5 mm，l=45 mm。

据试验数据[17]知，该履带车辆在翻越障碍工况下受到的冲击载荷最大，其平均冲击力为机重0.6倍，为最严酷工况，因此以此工况为例进行计算分析。此时，减振模型的输入为：

(29)

式中:g为重力常数，δ(t)为狄拉克δ函数。

将上述数据代入式(28)，依据数值算法在MATLAB环境下编程计算该履带车辆在翻越障碍工况下的动态响应。

3.3比较分析

分别采用有限元模型和分数阶减振模型对黏弹性悬架在翻越障碍工况下的动态响应进行计算，以车体振动和黏弹性件形变为考察对象，比较二者的计算结果，参见图7～8及表2。

图7　有限元计算云图Fig.7 Cloud maps of FEM

图8　车体振动响应Fig.8 Vibration response of vehicle body

分数阶减振模型计算结果中车体和悬架位移之差(x1-x2)为黏弹性件的压缩量或黏弹性悬架行程，则黏弹性件所受的应力为：

σ=kε+cDαε

(30)

(31)

根据分数阶导数线性性质得：

(32)

式中:[f]表示单位函数f(x)≡1，且

(33)

因此，黏弹性件所受应力可表示为：

(34)

表2　分数阶模型数值解与有限元解对比值

在翻越障碍受到冲击载荷后，车体响应迅速达到峰值，但由于黏弹性悬架的动能耗散作用，使车体响应快速衰减，在8 s时已经衰减了约81.6%，说明该黏弹性悬架具有较好缓冲减振能力。有限元结果显示，黏弹性件的最大压缩变形为25.79 mm，最大形变率为28.67%，节点最大应力为4.17 MPa，满足设计要求(压缩形变设计要求为13～76 mm，形变率设计要求为20%～75%)。

由图9与表2可知，分数阶减振模型数值解与有限元模型解吻合较好。在响应初始，分数阶减振模型计算结果的峰值大于有限元计算结果的峰值，这是因为分数阶减振模型在假设①的基础上建立，即上下黏弹性件接触面积A在悬架行程中保持不变，但在有限元模型中考虑了黏弹性件顶部弧度，在响应初始悬架行程较大，或出现“弹跳”现象，上下黏弹性件的接触由刚开始的点接触逐渐增加到定面A接触或反之，这样导致整个过程的平均接触面积小于数值模型的平均接触面积，进而导致有限元模型的接触压变大，故悬架行程峰值较大；在响应后期，分数阶减振模型和有限元计算结果较接近，这是因为振动已经被黏弹性悬架大幅过滤，悬架行程变小，有限元模型上下黏弹性件接触面积渐趋稳定，并接近静压接触面积A。另外，二者在最大压缩、最大形变率和最大应力计算值上相对误差均控制在10%内，分数阶减振模型数值方法满足实际工程的计算要求。

4　结　论

(1) 提出了基于FKV本构的黏弹性悬架分数阶减振模型及其数值方法，并和有限元计算结果进行了比较，结果证实两者具有较好的一致性，满足实际工程计算要求。

(2) 历史相关系数的变化特征表明分数阶减振模型具有全局相关性，整个历史响应会作用于瞬时响应，从基础层面体现了黏弹性悬架响应的历史依赖性和记忆性。

(3) 黏弹性悬架在车辆受到冲击载荷时，能快速将振动能转化为阻尼热而耗散，具有良好的减振性能，满足履带车辆在极端工况的支撑强度及稳定性要求。

(4) 为掌握低频重载下黏弹性材料的温频效应对悬架响应的影响，下一步将建立包含温频变量及分数阶数时间依赖性的减振模型及其数值方法，并开展DMA试验，绘制黏弹性材料的诺模图，对模型进行验证和修正，研究减振效果的参数敏感性。

[1] SONG Yong, SUN Dagang, ZHANG Xin, et al. An analytical solution to steady-state temperature distribution ofN-layer viscoelastic suspensions used in crawler vehicles[J]. International Journal of Heavy Vehicle Systems, 2012,19(3): 281-298.

[2] LUO Y, LIU Y, YIN H P. Numerical investigation of nonlinear properties of a rubber absorber in rail fastening systems[J]. International Journal of Mechanical Sciences, 2013,69(1): 107-113.

[3] 范让林，刘立，吕振华，等. 发动机隔振橡胶元件的有限元分析[J]. 内燃机学报,2009,27(2):186-191.

FAN Ranglin, LIU Li, LÜ Zhenhua, et al. Finite element analysis of engine vibration isolation rubber mount[J]. Transaction of CSICE,2009,27(2):186-191.

[4] 孙大刚，干奇银，杨兆民，等. 间隔阻尼层式支重轮缓冲性能分析[J]. 农业工程学报,2009,25(8):78-82.

SUN Dagang, GAN Qiyin, YANG Zhaomin，et al．Buffer property analysis of spaced-damping layer bogie wheel[J]．Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE),2009,25(8):78-82．

[5] ZHOU Y. Recent advances in fractional differential equations[J]. Applied Mathematics and Computation, 2015,257(1):1.

[6] SUN Limin, CHEN Lin. Free vibrations of a taut cable with a general viscoelastic damper modeled by fractional derivatives[J]. Journal of Sound and Vibration, 2015, 335(1): 19-33.

[7] CAFAGNA D. Fractional calculus: a mathematical tool from the past for present engineers: past and present[J]. Industrial Electronics Magazine, IEEE, 2007, 1(2): 35-40.

[8] 孙会来，金纯，张文明，等. 基于分数阶微积分的油气悬架建模与试验分析[J]. 振动与冲击, 2014, 33(17): 167-172.

SUN Huilai, JIN Chun, ZHANG Wenming, et al. Modeling and experimental analysis of hydro-pneumatic suspension based on fractional calculus[J]. Journal of Vibration and Shock, 2014, 33(17): 167-172.

[9] SPANOS P D, EVANGELATOS G I. Response of a non-linear system with restoring forces governed by fractional derivatives: time domain simulation and statistical linearization solution[J]. Soil Dynamics and Earthquake Engineering,2010,30(9):811-821.

[10] LUKASHCHUK S Y. An approximate solution method for ordinary fractional differential equations with the Riemann-Liouville fractional derivatives[J]. Communications in Nonlinear Science and Numerical Simulation,2014,19(2):390-400.

[11] BUTERA S, DI PAOLA M. A physically based connection between fractional calculus and fractal geometry[J]. Annals of Physics, 2014,350(10):146-158.

[12] ZOPF C, HOQUE S E, KALISKE M. Comparison of approaches to model viscoelasticity based on fractional time derivatives[J]. Computational Materials Science,2015,98(1):287-296.

[13] 贺少波,孙克辉,王会海. 分数阶混沌系统的Adomian分解法求解及其复杂性分析[J]. 物理学报,2014,63(3):58-65.

HE Shaobo, SUN Kehui, WANG Huihai. Solution of the fractional-order chaotic system based on Adomian decomposition algorithm and its complexity analysis[J]. Acta Physica Sinica,2014,63(3):58-65.

[14] ZHU Shengyang, CAI Chengbiao, SPANOS P D. A nonlinear and fractional derivative viscoelastic model for rail pads in the dynamic analysis of coupled vehicle-slab track systems[J].Journal of Sound and Vibration, 2015, 335(1): 304-320.

[15] UCHAIKIN V V. Fractional derivatives for physicists and engineers[M]. Beijing: Higher Education Press,2013:229-332.

[16] 孙大刚，宋勇，林慕义，等．黏弹性悬架阻尼缓冲件动态接触有限元建模研究[J]．农业工程学报，2008,24(1)：24-28．

SUN Dagang, SONG Yong, LIN Muyi, et al. Modeling of dynamic contact finite element method for damping buffer components mounted on viscoelastic suspensions[J]. Transactions of the Chinese Society of Agricultural Engineering:Transactions of the CSAE,2008,24(1):24-28.

[17] 孙大刚，诸文农，贡凯军.大型履带式推土机行走系阻尼减振的研究[J]. 机械工程学报,1998,34(1): 27-32.

SUN Dagang, ZHU Wennong, GONG Kaijun. Study on vibration damping isolations of undercarriages in heavy duty crawler-type bulldozers[J]. Journal of Mechanical Engineering, 1998,34(1):27-32.

A fractional calculus-based vibration suppression model and its numerical solution for viscoelastic suspension

LI Zhanlong1,2, SUN Dagang1,2, SONG Yong2, LIU Fuxi1, ZHAO Shuping2

(1. School of Mechanical and Precision Instrument Engineering, Xi’an University of Technology，Xi’an 710048, China;2. College of Mechanical Engineering, Taiyuan University of Science and Technology, Taiyuan 030024, China)

To obtain dynamic responses of viscoelastic suspension accurately, an FKV constitutive model of viscoelastic materials was developed by employing fractional derivative. A vibration model of viscoelastic suspension considering geometric factor was built based on FKV. Numerical solution was derived by employing Grumwald-Letnikov definition for fraction calculus and matrix function theory. Dynamic contact FEM was established based on a crawler vehicle that was installed viscoelastic suspension and used to compare with the fractional method. Results show that the fractional vibration control model can embody the nonlocal correlation and memory feature of viscoelastic suspension which exhibits excellent vibration control capability. The numerical result shows good agreement with that from the FEM. The study provides essential theoretical references for future in-situ tests and practice applications.

factional calculus; viscoelastic suspension; vibration control model; numerical method

国家青年科学基金(51305288); 山西省回国留学人员科研资助项目(2012-073); 山西省青年科学基金(2013021020-1)

2015-05-14修改稿收到日期：2015-07-27

李占龙 男，博士生，1985年11月生

孙大刚 男，教授，博士生导师，1955年4月生

U461.4

A

10.13465/j.cnki.jvs.2016.16.020