Generalized Sheffer-stroke Based Analytic Modal Axiomatic System for GL*

Fangfang Tang

Institution of Marxism Research，Chinese Academy of Social Sciences tangff@cass.org.cn



Generalized Sheffer-stroke Based Analytic Modal Axiomatic System for GL*

Fangfang Tang

Institution of Marxism Research，Chinese Academy of Social Sciences tangff@cass.org.cn

Abstract.Based on Generalized Sheffer-stroke，this paper proposes modal tableau and analytic axiomatic system for the modal logic GL.Generalized Sheffer-stroke is a kind of n-ary operator which provides a new notation for formulas of modal logic，and makes it convenient to express the analytic axiomatic systems.The rules of modal tableau based on the new operator are different from the ones based on ordinary connectives and modality.The analytic axiomatic system has simple proof procedure.The correspondence between modal tableau and analytic axiomatic system makes it easy to show the completeness of the analytic axiomatic system for GL in terms of the results of modal tableau GL.The proof of Completeness Theorem of modal system for GL is special，for the method of canonical model can not be used directly，and then we use a method to filter some possible worlds and get a finite model.

1　Introduction and Overview

An axiomatic system is called analytic，if the premises and consequences of its primitive inferential rules share propositional variables.Analytic axiomatic system （AAS）of propositional logic was originally proposed by Anderson and Belnap（［1］）and named AB by Hunter（［3］）.The system AB is special，for its inferential rules based on its primitive connectives，negation and disjunction，and although it has no the Rule of Modus Ponens（sometimes also called the Rule of Detachment：if A and ¬A∨B are theorems，so is B），it has simple proof procedure.Qingyu Zhang proposed an analytic axiomatic system of propositional logic named Z，which modified the system AB with a kind of new n-ary operator（Generalized NAND）as the only primitive connective and showed that the proofs of Completeness Theorem，Independence Theorem and Interpolation Theorem are simple.（［6，7］）We try to extend analytic axiomatic systems from propositional logic to modal logic.We have defined a new n-ary operator named Generalized Sheffer-stroke，which is a hybrid of Generalized NAND and modality，and propose analytic axiomatic systems for some normal modal logics K，T，D，K4，D4，S4（［5］）and S5（［4］），which are a variant of modal tableaus of Fitting and hypersequents of Arnon Avron.（［2］）

This paper will propose modal tableau and the AAS for the modal logic GL basedonGeneralizedSheffer-stroke，andshowthattheAAS forGLhassimpleproof procedure.Since Generalized Sheffer-stroke is a new operator，on which the rules of modal tableau system GL based are different from the ones based on ordinary connectives and modality.（［2］）The proof of Completeness Theorem of system GL isspecial，forthemethodofcanonicalmodelcannotbeuseddirectly.ModallogicGL is a proper extension of modal logic K（or K4），containing the Löb formula□（□p→p）→ □p.The formulas of GL are valid on two classes of frames，the class of transitive and upwards well-found frames，noted GLω，and the class of transitive，irreflexive and finite frames，noted GLf.Because a frame of GLfis finite，and the canonical model is infinite，the canonical model of GL is not a model on a frame of GLf.Then we use a method of filter to pick out some possible worlds，and get a finite model.

2　Basic Syntax and Semantics

The formal language of modal logic defined in this paper，named bracket modal language，has two kinds of primitive symbols：

1.Propositional variables：p0，p1，...

2.Modal bracket：［；］.

Definition 1Modal bracket［；］is a n-ary operator and n is not fixed.

The following is the definition of well-formed formulas of the basic modal language：

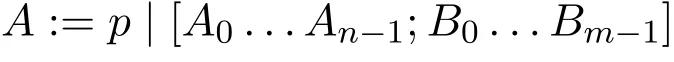
where p ranges over elements of the set of propositional variables P，and n≥0，m≥0.

By this definition，when n，m=0，we get a modal formula［；］.When m=0，modal formulas have the form［A0...An−1；］and let them be simplified as［A0... An−1］.When n=0，modal formulas have the form［；B0...Bm−1］and let them be simplifiedas〈B0...Bm−1〉.LetΓ（or∆）refertoasequenceofformulasA0...An−1，and then formulas［A0...An−1；B0...Bm−1］could be abbreviated as［Γ；∆］.

Definition 2For any formulas，the sum of left brackets occur in it is equal to the sumoftherightbracketsoccur，whichisusedtodecidethedegreeoftheformula.The degree of a formula A，noted Dg（A），is inductively defined by the following rules

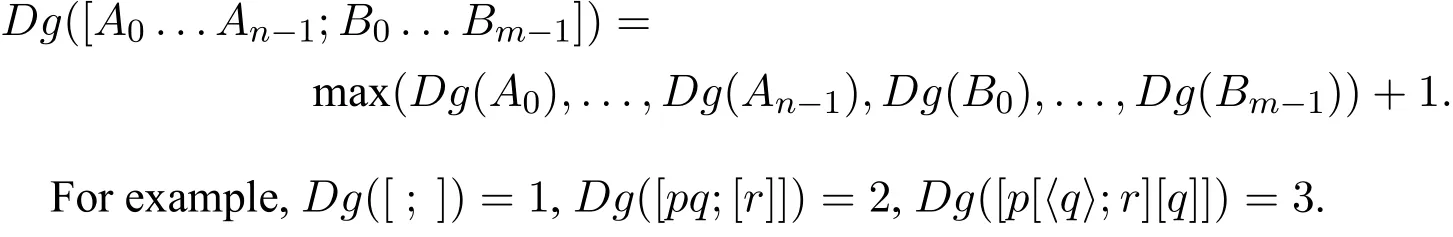
Definition3Awell-formedformulaB whichoccursasaconsecutivepartofawellformed formula A，will be known as a subformula of A，which is noted B∈sub（A）. Thedirectsubformulasofformula［A0...An−1；B0...Bm−1］areA0，...，An−1，B0，...，Bm−1.The set of subformulas of a formula A，noted sub（A），is inductively defined by the following rules：

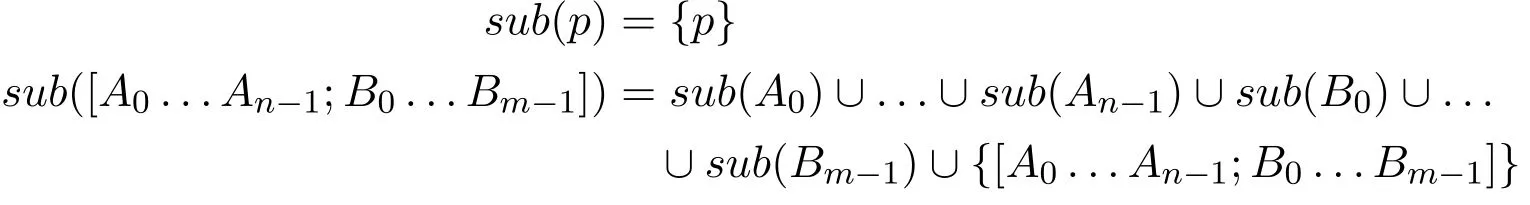
A Kripke frame is a pair（W，R），where W（set of worlds）is a non-empty set and R（accessibility）is a binary relation，i.e.R⊆W×W.If F=（W，R）is a Kripke frame，then M=（W，R，V）is a Kripke model on the frame F，where V（valuation）is a map from the set of propositional variables P to the power set of the set W.

Definition 4（Truth Condition）Suppose M=（W，R，V）is a Kripke model，and w∈W.

1.M，w|=p iff w∈V（p）；

2.M，w|=［A0...An−1；B0...Bm−1］iff there is i＜n，s.t.M，w⊭Ai，or there are j＜m and w∗∈W，s.t.wRw∗and M，w∗⊭Bj.

Bydefinitionabove，GeneralizedSheffer-strokecandefineconnectivesandmodalities：

All ordinary formulas of basic modal language could be translated to formulas of bracket modal language.For example，the Löb formula□（□p→p）→□p could be translated to a formula of bracket modal language step by step：

And by the definition above，［［〈［［〈p〉］［p］］〉］［［〈p〉］］］is semantically equivalent with［［〈［［〈p〉］［p］］〉］〈p〉］，and then semantically equivalent with［〈p〉；［［〈p〉］［p］］］.

3　Modal Tableau System for GL

This section will propose a modal tableau system for modal logic GL.Analytic axiomatic system for GL in the next section is based on modal tableau for GL. Tableaus usually are analytic，i.e.all formulas occurring in a proof share the same propositionalvariablesoccurringintheformulasbeingproved，whichmakesthefinding of proofs a simple thing.Tableaus take the form of trees with the root at the top and branching downward.Formulas added at the end of a branch of a tableau are all be obtained by applying a tableau rule on formulas occurring in the same branch.

BasedonthenewoperatorGeneralizedSheffer-stroke，modaltableausaredifferentfromonesbasedonordinaryconnectivesandmodality.ThemodaltableauforGL includes three tableau rules：［；］-rule（figure 1），［［；］］-rule（figure 2）and〈〉-GL rule （table 1）.The〈〉-GL rule is destructive：any branch S which includes formulas with the form〈A0...An−1〉is replaced with a new branch S#∪｛［〈A0...An−1〉］，［A0... An−1］｝，where the definition of S#for GL follows such that for a Kripke model M=（W，R，V），for any w，w∗∈W，if M，w|=S and wRw∗，then M，w∗|=S#.

Definition 5S#=｛［［A0...An−1］］，［〈A0...An−1〉］|［〈A0...An−1〉］∈S｝.

By the definition above，we have some facts：

1.If S1⊆S2，then S#1⊆S#2.

2.S#⊆S##.

Figure 1：［；］-rule

Figure 2：［［；］］-rule

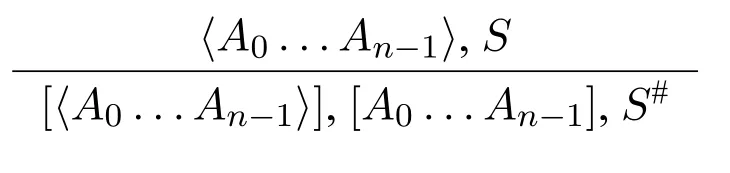
Table 1：〈〉-GL rule

Figure 3：A Proof in tableau system of GL

Theorem 1Suppose M=（W，R，V）is a Kripke model，S is a set of formulas，w∗∈W is a possible world accessible from w.We have：

1.If M，w|=S，then M，w∗|=｛［［A0...An−1］］|［〈A0...An−1〉］∈S｝.

2.If R is transitive，then

3.If M is a Kripke model of GL，then if M，w|=S，then M，w∗|=S#.

Proof1.By truth condition.

2.Given any w1∈W，s.t.w∗Rw1.Because R is transitive，wRw1.

Suppose M，w|=S.Given［〈A0...An−1〉］∈S，we have

M，w|=［〈A0...An−1〉］.Then M，w1|=［［A0...An−1］］by（1）.

Hence，M，w∗|=［〈A0...An−1〉］.

3.By the definition of S#，from（1）and（2）.

A GL-tableau proof of the Löb formula［［〈［［〈p〉］［p］］〉］〈p〉］is shown in figure 3，where formula 2 and formula 3 are added to the branch by［［；］］-rule from formula 1.Since formula 3 has the form〈A0...An−1〉and n=1，the〈〉-GL rule could be applied on it.Then the branch is replaced with a new branch including formulas 4，5，6 and 7.Then 8 is added to the new branch by［［；］］-rule from 7.By applying［；］-rule on 8，two branches grow，at the end of which formulas 9 and 10 are added respectively，and then both of the branches are closed.

Theorem 2Suppose T is a GLω-satisfiable tableau，and T′is a tableau which is obtained by applying a tableau rule once on the tableau T，then T′is also GLωsatisfiable.

ProofSuppose T is a GLω-satisfiable tableau，then there is a branch θ in T is GLωsatisfiable.Let a GL-tableau rule is applied on this branch.It will show that each of GL-tableau rules preserve GLω-satisfiable.

·The［；］-rule case.Suppose the set of all formulas in the branch θ is S∪｛［A0... An−1；B0...Bm−1］｝.Then［；］-rulecouldbeappliedonthisbranch，fromwhichn+ 1newbranchesgrow，notedθi，where0≤i＜n+1.Inthenewbranches，thesetofall formulas in a new branch θi＜nis S∪｛［A0...An−1；B0...Bm−1］，［Ai］｝，and the set ofallformulasinnewbranchθnisS∪｛［A0...An−1；B0...Bm−1］，〈B0...Bm−1〉｝. Because θ is GLω-satisfiable，there is a GL-model M=（W，R，V）and a possible world w∈W，s.t.M，w|=S∪｛［A0...An−1；B0...Bm−1］｝.

Because M，w|=［A0...An−1；B0...Bm−1］，by truth condition，there is 0≤i＜n，s.t.M，w|=［Ai］or M，w|=〈B0...Bm−1〉.

Then，there is i＜n，s.t.M，w|=S∪｛［A0...An−1；B0...Bm−1］，［Ai］｝or M，w|= S∪｛［A0...An−1；B0...Bm−1］，〈B0...Bm−1〉｝.

·The［［；］］-rule case.By truth condition，similarly.

·The〈〉-GL rule case.If a GLω-satisfiable branch θ of tableau T includes a formula 〈A0...An−1〉，and the set of all formulas in the branch θ is noted S，then〈〉-GL rule may be applied on this branch，which is then replaced with a new branch θ′.The set of all formulas in θ′is S#∪｛［〈A0...An−1〉］，［A0...An−1］｝.We need to prove that if there is a GLω-model M=（W，R，V）and a world w∈W，such that M，w|=S and M，w|=〈A0...An−1〉，then there is v∈W，such that M，v|=S#，and

SupposethereisaGLωmodelM=（W，R，V）andaworldw1∈W，s.t.M，w1|=S andM，w1|=〈A0...An−1〉，andanyv∈W，M，v⊭S#∪｛［〈A0...An−1〉］，［A0...An−1］｝

Because M，w1|=〈A0...An−1〉，by the definition of〈〉，we have：

there is w2∈W，w1Rw2and M，w2|=［A0...An−1］.

Because M，w1|=S，w1Rw2and R is transitive，we have M，w2|=S#.Because M，w2⊭S#∪｛［〈A0...An−1〉］，［A0...An−1］｝，we have M，w2⊭［〈A0...An−1〉］. Hence M，w2|=〈A0...An−1〉.Therefore M，w2|=S#∪｛〈A0...An−1〉，［A0... An−1］｝.Because M，w2|=〈A0...An−1〉，by truth condition，we have：

there is w3∈W，w2Rw3and M，w3|=［A0...An−1］.Since M，w2|=S#，w2Rw3and R is transitive，M，w3|=S##.By the definition of S#for GL，S#⊆S##.Hence，M，w3|=S#.Therefore M，w3|=S#∪｛〈A0...An−1〉，［A0...An−1］｝.Similarly，there is w4，s.t.w3Rw4，and M，w4|= S#∪｛〈A0...An−1〉，［A0...An−1］｝.Then，there is an infinite chain

ButGLω-modelsareallupwardswell-found.Contradition.Therefore，ifS∪｛〈A0... An−1〉｝is GLω-satisfiable，then S#∪｛［〈A0...An−1〉］，［A0...An−1］｝is also GLωsatisfiable.

Theorem 3（Soundness）If formula A has a GL-tableau proof，then A is valid on all of the GL-models（frames）.

ProofSupposeAisnotvalidonalloftheGL-models（frames），thenthereisamodel M=（W，R，V）based on a frame of GLωand a world w∈W，such that M，w⊭A. Then｛［A］｝is GLω-satisfiable.For any formula A，the GL-tableau proof of A is a tree growing from the root｛［A］｝.Since｛［A］｝is GLω-satisfiable，by the theorem above，tableaus constructed from｛［A］｝are all GLω-satisfiable.A GLω-satisfiable tableau is not closed.Therefore，formula A has no GL-tableau proof.

Theorem 4（Completeness）If a formula Z is valid on all models based on GL-frames，then Z has a GL-tableau proof.

ProofLet Z is a modal formula which has no GL-tableau proof.Define Sub（Z）= ｛A，［A］|A is a subformula of Z｝.Sub（Z）is a finite set.A set of formulas is called GL-consistent，if there is no close GL-tableau for any finite subset of its subformulas.For any Sub（Z），its GL-consistent subset S could be extended to a maximally GL-consistent set by Lindenbaum construction.

Define Wz=｛w|w is a maximally GL-consistent set which is extended from a GL-consistent subset of Sub（Z）｝.For any w1，w2∈Wz，if w#1⊆w2，then let w1R0w2.For any w1，w2∈Wz，if w1R0w2and not w2R0w1，then let w1RZw2.Finally，if p∈w，then let w∈Vz（p）.Then a model Mz=（Wz，Rz，Vz）is constructed. Clearly，Wzis finite.Rzis irreflexive by its definition.It is easy to prove that Rzis transitive，by the definition of R0and Rzand by the facts about w#.Therefore，Mzis a model based on a frame of GLf（a GLf-model）.

Now we prove the fact：for any w∈Wz，for any formula A∈Sub（Z），

Induction on the degree of formula Z，namely Dg（Z）：

1.Suppose Dg（Z）=0，i.e.Z is p.Sub（Z）=Sub（p）=｛p，［p］｝.

If p∈w，by the definition of Vz，we have w∈Vz（p），then Mz，w|=p.

If［p］∈w，since w is maximally GL-consistent，p/∈w.So w/∈Vz（p）.Then Mz，w⊭p.Then Mz，w|=［p］.

2.Suppose Dg（Z）=n（n≥0），i.e.Z has the form［A0...An−1；B0...Bm−1］，and

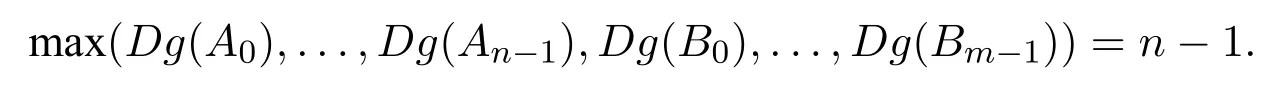
If［A0...An−1；B0...Bm−1］∈w，thenby［；］-ruleandthemaximalGL-consistency of w，there is i＜n，［Ai］∈w or〈B0...Bm−1〉∈w.

If there is i＜n，［Ai］∈w.By inductive hypothesis，we have Mz，w|=［Ai］.

If〈B0...Bm−1〉∈w，thenw#∪｛［〈B0...Bm−1〉］，［B0...Bm−1］｝isGL-consistent，by〈〉-GL rule.Let w∗is a maximally GL-consistent set extended from w#∪｛［〈B0 ...Bm−1〉］，［B0...Bm−1］｝，then w∗∈W，w#⊆ w∗.By the definition of R0，wR0w∗.Since［〈B0...Bm−1〉］∈w∗，bydefinitionofw#，wehave［〈B0...Bm−1〉］∈w∗#.Since〈B0...Bm−1〉∈w，and w is GL-consistent，we have［〈B0...Bm−1〉］/∈w.Hence not w∗#⊆ w，by definition of R0，not w∗R0w.Then wRzw∗.Since ［B0...Bm−1］∈w∗，by［；］-rule，there is j＜m，w∗∪｛［Bj］｝is GL-consistent. Then［Bj］∈w∗.Hence by inductive hypothesis，Mz，w∗|=［Bj］.Therefore，

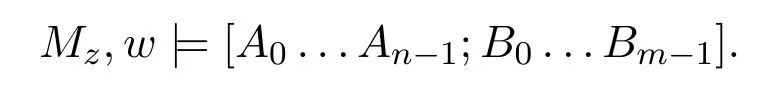
If［［A0...An−1；B0...Bm−1］］∈w，then by［［；］］-rule，we have

w∪｛A0，...，An−1，［〈B0...Bm−1〉］｝is GL-consistent.

By the maximal GL-consistency of w，for any i＜n，

Ai∈w and［〈B0...Bm−1〉］∈w.

Since Ai∈w，by inductive hypothesis，Mz，w|=Ai.

Since［〈B0...Bm−1〉］∈w，［［B0...Bm−1］］∈w#by definition of w#.Let w∗∈W，s.t.wRzw∗.By definition of Rz，we have w#⊆w∗.Then［［B0...Bm−1］］∈w∗.

By［［；］］-rule，for any j＜m，we have Bj∈w∗by the maximal GL-consistency of w∗.By inductive hypothesis，Mz，w∗|=Bj.Therefore，for any i＜n，Mz，w|=Ai，and for any w∗∈W，if wRzw∗，then for any j＜m，Mz，w∗|=Bj.Hence，

Since Z has no GL-tableau proof，then there is no closed GL-tableau of｛［Z］｝，i.e.｛［Z］｝is GL-consistent.Because［Z］∈Sub（Z），｛［Z］｝is a GL-consistent subset of Sub（Z），which could be extended to a maximally GL-consistent set w∈Wz，［Z］∈w.Then Mz，w|=［Z］，and then we have Mz，w⊭Z.Therefore，Z is not

valid on all GLf-models.

Therefore，Z is not valid on all models based on GL-frames.

4　Analytic Axiomatic System for Modal Logic GL

Based on the new notation，analytic axiomatic system AAS for modal logic GL couldbeconstructed.TheaxiomsoftheAAS forGLhavetwokindsofforms，where Γ or∆，a sequence of modal formulas，could be an empty sequence：

1.Axiom 1：［ΓA［A］∆］

2.Axiom 2：［Γ［；］∆］

The inferential rules of AAS for GL include the classical inferential rules，［；］-rule and［［；］］-rule（in table 2），and modal inferential rule，G-rule（in table 3）.For the modal inferential rule G-rule（in table 3），Γ♯is defined indirectly：

Firstly，|Γ|is the set｛Ai|Aiis a formula occurring in the sequence Γ｝.

Secondly，|Γ|♯=｛［［A0...An−1］］，［〈A0...An−1〉］|［〈A0...An−1〉］∈|Γ|｝.

Finally，Γ♯is a sequence of all formulas in|Γ|♯.

Table 2：Classical Inferential Rules

Table 3：Modal Inferential Rule：G-rule

From the primitive inferential rules above（in table 2 and table 3），some useful derived rules follow（in table 4）.The rule I and rule II are the special forms of the［；］-rule and the［［；］］-rule（in table 2）respectively.

For any analytic axiomatic system L，the L-proof of is a sequence of formulas A0，...，An−1，where Aiis either an axiom of L or derived by a inferential rule of Lfrom a formula Aj（j＜i）.And formula A is L-provable，if there is an L-proof in which the final formula is［［A］］（semantic equivalent to A）.

Table 4：Derived Rules

An example of a GL-proof of the Löb formula［〈p〉；［［〈p〉］［p］］］follows（table 5）.

Table 5：a GL-Proof Example

The process of finding the proof is from bottom to top.Firstly，for the Löb formula A=［〈p〉；［［〈p〉］［p］］］，there are direct subformulas at the right side of the semicolon，then we could get［［A］］by the inferential［［；］］-rule.Hence，we could obtain formula 6 from formula 5.Secondly，because formula 5，［［〈［［〈p〉］［p］］〉］〈p〉］，has a direct subformula〈p〉，only G-rule could be applied.So we must get formula 4 before wegetformula5.Thirdly，wefoundthat［［［［〈p〉］［p］］］］isadirectsubformulaofformula 4，which could be obtained by applying Derived Rule II，then we must get formula 3 before we get formula 4.Then，for formula［［〈p〉］［p］］is a direct subformula of 3，the Derived Rule I could be applied，so the provability of formula 3 could be reduced to the provability of formula 1 and formula 2，which are both axioms.

Now we prove the completeness theorem of system GL.

Theorem 5（Completeness）Let A is a modal formula.

1.If A is GL-provable，then A is valid on all models based on GL-frames.

2.If A is valid on all models based on GL-frames，then A is GL-provable.

Proof

1.Axioms of GL are tautologies and so are valid on every model based on a frame of GLω.

It's easy to prove that the classical inferential rules of analytic axiomatic system GL preserve GLω-validity.Only consider G-rule here.

Suppose［Γ♯［A0...An−1］［〈A0...An−1〉］∆♯］is valid on any model based on a frame of GLω（GLω-model），and there is a GLω-model M=（W，R，V），and w1∈W，s.t.

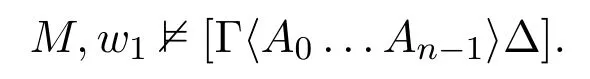
By truth condition，M，w1|=|Γ|∪|∆|∪｛〈A0...An−1〉｝.Then，there is an infinite chain：

But GLω-models are all upwards well-found.Contradiction.Hence the G-rule preserve GLω-validity.

2.Suppose formula A is valid on every model based on a frame of GLf.By the completeness theorem of the tableau system of GL，A has a GL-tableau proof，i.e. there is a closed GL-tableau of｛［A］｝.We define a mapping from a finite set of modal formulas to a modal formula

Claim：Let S is a finite set of formulas.For S，if there is a closed GL-tableau of S，then Ssis GL-provable.

Suppose there is a closed GL-tableau of S，using the tableau rules of GL for at least d times.Induction on d.

If d=0，then some modal formula A and its negation［A］are both in the set S，or［；］∈S.Then Ssis a axiom of analytic axiomatic system of GL.Therefore，Ssis GL-provable.

If d=k＞0.Here only consider the tableau〈〉-rule case.

Suppose〈A0...An−1〉∈S，and the closed tableau use the〈〉-rule of GL firstly，and using the tableau rules of GL for d times.Then there is a closed tableau of S♯∪｛［〈A0...An−1〉］，［A0...An−1］｝，using the tableau rules less than d times.By inductive hypothesis，［Γ♯［A0...，An−1］［〈A0...An−1〉］∆♯］is GL-provable，where |Γ♯|∪|∆♯|=S♯.By the G-rule，［Γ〈A0...An−1〉∆］is GL-provable，and|Γ|∪|∆|= S.Therefore，Ssis GL-provable.

5　Conclusion

Generalized Sheffer-stroke is a kind of n-ary operator which provides a new notation for formulas of modal logic.The formulas which have the form［A0...An−1；］are formulas of propositional logic.The formula［A0...An−1；B0...Bm−1］is semantically equivalent to¬A0∨...∨¬An−1∨◇（¬B0∨...∨¬Bm−1）.The new notation is convenient to express the analytic axiomatic systems（AAS），and the nary operator saves primitive connectives and parentheses，that is，the modal bracket［；］could define all propositional connectives such as negative and disjunctive，and the new notation needs no parentheses.

Based on the Generalized Sheffer-stroke，I propose destructive modal tableau system and analytic axiomatic system for the modal logic GL in this paper.Since the Generalized Sheffer-stroke is a new operator，on which the rules of modal tableau GL based are different from the ones based on ordinary connectives and modality. The correspondence between modal tableau and analytic axiomatic system makes it easy to show the completeness of the analytic axiomatic system GL in terms of the results of modal tableau GL.The proof of Completeness Theorem of AAS for GL is special.Since the formulas of GL are valid in the class of frames GLf，on which the models are finite，and the canonical model is infinite，the method of canonical model can not be used directly in the proof.But we could use a method to filter some possible worlds，and get a finite model.

In this paper，it is showed that AAS for modal logic GL based on Generalized Sheffer-stroke is concise.In such a system，a proof of a formula of modal logic GL is easy to be found，and based on the results of modal tableau，the proof the Completeness Theorem is simple.And the AAS could be extended from the system AB and Z for propositional logic to some modal logics，including the modal logic GL.

References

［1］ A.R.AndersonandN.D.Belnap，1959，“Asimpletreatmentoftruthfunctions”，Journal of Symbolic Logic，24（4）：301-302.

［2］ P.Blackburn，2007，Handbook of Modal Logic，Amsterdam：Elsevier.

［3］ G.Hunter，1971，Metalogic：An Introduction to the Metatheory of Standard First Order Logic，Berkeley：University of California Press.

［4］ F.Tang，2009，“Generalized Sheffer-stroke based analytical modal axiomatic systems”，Studies in Logic，2（3）：37-49.

［5］ F.Tang，2009，“Modalaxiomaticsystemsbasedondestructivemodaltableaus”，Journal of Hunan University of Science and Technology（Social Science Edition），12（1）：41-48.

［6］ Q.Zhang，1997，“An axiomatic system of classical propositional logic”，Philosophical Researches，8：51-58.

［7］ Q.Zhang，1999，“The normal form and interpolation theorem of system Z”，Philosophical Researches，12：74-78.

2015-11-12

*I would like to thank Professor QingYu Zhang for his efforts helping me to work on analytic axiomatic systems.