具有Neumann边界条件的非局部多孔体介质方程解的爆破时间下界估计*

方钟波, 柴　艳

(中国海洋大学数学科学学院，山东 青岛 266100)



具有Neumann边界条件的非局部多孔体介质方程解的爆破时间下界估计*

方钟波, 柴艳

(中国海洋大学数学科学学院，山东 青岛 266100)

本文中研究一类具有非齐次Neumann边界条件的非局部多孔体介质方程解的爆破现象。对边界流为线性源及线性吸收情形，利用微分不等式技巧得到解发生爆破时爆破时间下界估计值。

多孔体介质方程；非局部源；Neumann边界条件；爆破时间下界

引用格式：方钟波, 柴艳. 具有Neumann边界条件的非局部多孔体介质方程解的爆破时间下界估计[J]. 中国海洋大学学报(自然科学版), 2016, 46(9): 129-132.

FANGZhong-Bo，CHAIYan.Lowerboundsestimatesoftheblow-uptimeforanonlinearnonlocalporousmediumequationwithNeumannboundarycondition[J].PeriodicalofOceanUniversityofChina, 2016, 46(9): 129-132.

考虑一类具有非局部源与非齐次Neumann边界条件的多孔体介质方程初边值问题

ut=Δum+up∫Ωuqdx,(x,t)∈Ω×(0,T),

(1)

(2)

u(x,0)=u0(x),x∈Ω,

(3)

其中:Ω⊂R3是具有光滑边界∂Ω的有界区域;p≥0;q>0;p+q>m>1;k是常数;ν是∂Ω上的单位外法线向量;T是可能发生爆破的时间。

方程(1)描述流体力学、人口动力学及生物群体力学等诸多领域中扩散现象[1-2]。从流体力学角度来说，描述牛顿流在多孔体介质中的流动，其中up∫Ωuqdx叫“非局部热源”项，非线性边界流(2)中系数k为正或负时分别称为“线性源”或“线性吸收”边界流。

对抛物型方程(组)解的爆破现象的研究已有许多文献和专著，见文献[3-4]及相关文献。但是，这些文献讨论的问题是关于解的整体存在性与非存在性及渐近性质相关的问题。最近，此类问题中爆破解的爆破时间上下界估计值的计算方面也引起了许多学者和专家的广泛关注。其实，爆破时间上界估计方面已有较好的成果，比如Levine[5]介绍的凸性方法，Gao等[6]介绍的辅助函数法、极值原理和上下解方法相结合的方法等。相对而言，爆破时间下界估计更难。Song[7]研究了研究了具有非局部源项和吸收项的半线性扩散方程

ut=Δu+∫Ωupdx-kuq, (x,t)∈Ω×(0,T),

其中p>q>1。他们利用微分不等式的技巧，在齐次Dirichlet边界条件或齐次Neumann边界条件下得到了爆破时间的下界。之后，Liu等[8]和Fang等[9]采用类似的方法，考虑了具有非局部源项和吸收项的拟线性抛物型方程，并得到了爆破时间下界估计值。

由上所知，具有非齐次Neumann边界条件的非局部多孔体介质方程初边值问题(1)～(3)中爆破解的爆破时间下界估计的研究还未得到展开。此类问题的难度在于文献[7-9]中采用的微分不等式技巧不再适用于问题(1)～(3)等。本文，对边界流为线性源及线性吸收情形，利用改进的微分不等式技巧得到爆破时间下界估计值。实际上，当p+q>m>1且初始值充分大时，类似于文献[10]方法易得问题(1)～(3)解在有限时刻T爆破。

注意到，由Sobolev型不等式的最优化常数，导致所得的结果仅局限在三维空间，见文献[13]。同时，此类问题的研究对于发展方程解的生命跨度的确定有着非常重要的意义。

1　当k>0时爆破时间T的下界

定义辅助函数

η(t)=∫Ωuα(p+q-1)dx,

(4)

η′(t)=α(p+q-1)∫Ωuα(p+q-1)-1utdx=

α(p+q-1)∫Ωuα(p+q-1)-1[Δum+up∫Ωuqdx]dx=

kα(p+q-1)∫∂Ωuα(p+q-1)dS-

mα(p+q-1)[α(p+q-1)-1]∫Ωuα(p+q-1)+m-3

(5)

由积分等式

div(uα(p+q-1)x)=3uα(p+q-1)+α(p+q-1)uα(p+q-1)-1(x·▽u)

可得

(6)

再由Schwarz不等式得

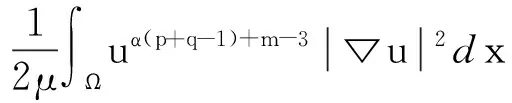
(7)

把(6)，(7)带入(5)得

{mα(p+q-1)[α(p+q-1)-1]-

α(p+q-1)∫Ωuα(p+q-1)+p-1dx∫Ωuqdx。

(8)

利用Hölder不等式可知

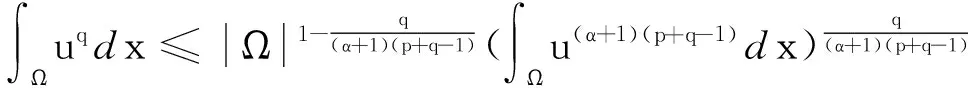
(9)

∫Ωuα(p+q-1)+p-1dx ≤

(10)

(11)

又

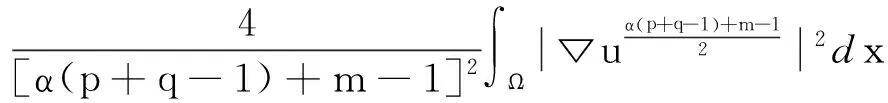
(12)

把(9)-(12)带入(8)有

(13)

其中

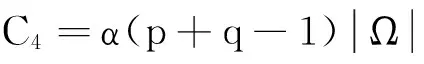
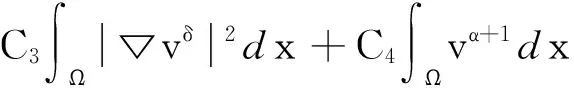
(14)

(15)

类似于[12]中(2.28)式的推导得

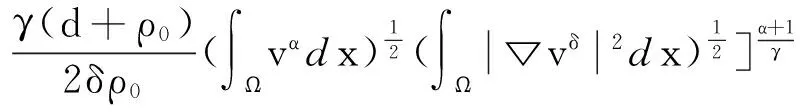
(16)

用Hölder不等式得

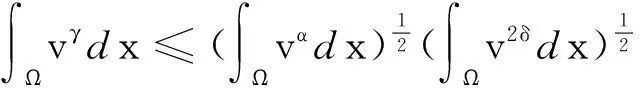
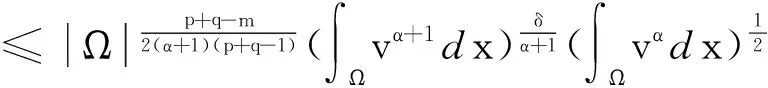
(17)

把(17)带入(16)且应用下列不等式

得

(18)

由(15)及(18)可知

∫Ωvα+1dx≤

(19)

∫Ωvα+1dx≤

(20)

其中κ1，κ2>0待定。由(20)可以得出

(21)

其中

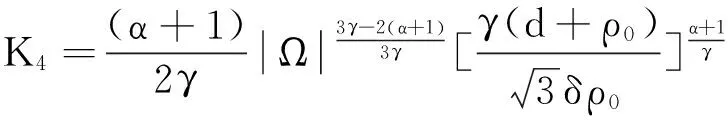
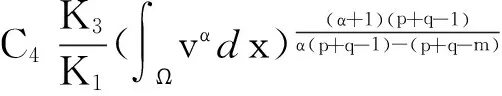
(22)

记

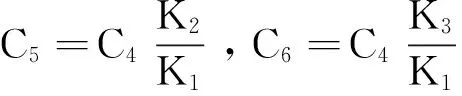
则(22)式可简写成

(23)

在(0,t)积分(23)得

其中

2　当k≤0时爆破时间T的下界

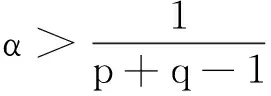
对η(t)求导，并由(2)及k≤0，可得

η′(t)=α(p+q-1)∫Ωuα(p+q-1)-1utdx=

α(p+q-1)∫Ωuα(p+q-1)-1[Δum+up∫Ωuqdx]dx=

kα(p+q-1)∫∂Ωuα(p+q-1)dS-

mα(p+q-1)[α(p+q-1)-

α(p+q-1)∫Ωuα(p+q-1)+p-1dx∫Ωuqdx≤

-mα(p+q-1)[α(p+q-1)-

(24)

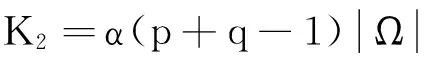
类似于定理1的证明过程，可得

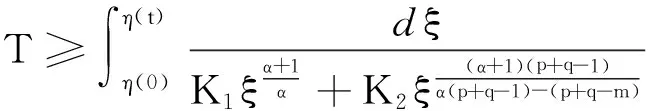
因此，可以建立下面的定理。

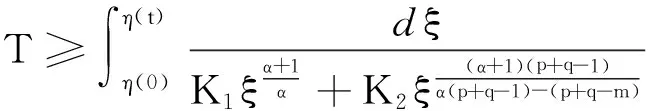
[1]Bebernes J ，Eberly D. Mathematical Problems from Combustion Theory [M]. New York：Springer-Verlag, 1989.

[2]Wu Z, Zhao J, Yin J，et al. Nonlinear Diffusion Equations [M].Singapore: World Scientific, 2001.

[3]Levine H A. The role of critical exponents in blow-up theorems [J]. SIAM Rev, 1990, 32: 262-288.

[4]Samarskii A A, Kurdyumov S P, Galaktionov V A , et al. Blow-up in Problems for Quasilinear Parabolic Equations [M]. Moscow: Nauka, 1987, Berlin: Walter de Gruyter, 1995.

[5]Levine H A. Nonexistence of global weak solutions to some properly and improperly posed problems of mathematical physics: The method of unbounded fourier coefficients [J]. Math Ann, 1975, 214: 205-220.

[6]Gao X, Ding J, Guo B Z. Blow up and global solutions for quasilinear parabolic equations with Neumann boundary conditions [J]. Applicable Analysis, 2009, 88: 183-191.

[7]Song J C. Lower bounds for the blow-up time in a non-local reaction-diffusion problem [J]. Applied Mathematics Letter, 2011,24: 793-796.

[8]Liu D, Mu C, Xin Q. Lower bounds estimate for the blow-up time of a nonlinear porous medium equation [J]. Acta Mathematica Scientia, 2012, 32B(3): 1206-1212.

[9]Fang Z B, Yang R, Chai Y. Lower bounds estimate for the blow-up time of a slow diffusion equation with nonlocal source and inner absorption [J]. Mathematical Problems in Engineering, 2014 ,42: ID764248: 6.

[10]Li F, Xie C. Global existence and blow-up for a nonlinear porous medium equation [J]. Appl Math Lett, 2003, 16: 185-192.

[11]Talenti G. Best constant in Sobolev inequality [J]. Ann Mat Pura Appl, 1976, 110(1): 353-372.

[12]Li Y, Liu Y , Lin C. Blow-up phenomena for some nonlinear parabolic problems under mixed boundary conditions [J]. Nonliner Anal Real World Appl, 2010, 11: 3815-3823.

AMSSubjectClassifications：35R45; 35K65

责任编辑陈呈超

Lower Bounds Estimates of the Blow-up Time for a Nonlinear NonlocalPorousMediumEquationwithNeumannBoundaryCondition

FANGZhong-Bo，CHAIYan

(SchoolofMathematicalSciences,OceanUniversityofChina,Qingdao266100,China)

Inthispaper,theblow-upphenomenaofanonlinearnonlocalporousmediumequationwithnonhomogeneousNeumannboundaryconditionareinvestigated.Byusingadifferentialinequalitytechnique,lowerboundsestimatesoftheblow-uptimeareobtainedwhenboundaryfluxislinearsourceorlinearabsorption.

porousmediumequation;nonlocalsource;Neumannboundarycondition;thelowerboundofblow-uptime

山东省自然科学基金项目(ZR2012AM018)；中央高校基本科研基金项目(201362032)资助

2014-03-20；

2014-10-12

方钟波(1968-)，男，教授。E-mail:fangzb7777@hotmail.com

O175

A

1672-5174(2016)09-129-04

10.16441/j.cnki.hdxb.20140082

SupportedbytheNaturalScienceFoundationofShandongProvinceofChina(ZR2012AM018)andtheFundamentalResearchFundsfortheCentralUniversity(201362032)