鞅差误差下部分函数线性模型的经验似然推断
江志强,范国良
(安徽工程大学 数理学院,安徽 芜湖 241000)

鞅差误差下部分函数线性模型的经验似然推断
江志强,范国良*
(安徽工程大学 数理学院,安徽 芜湖 241000)
研究了误差是鞅差序列下的部分函数线性回归模型的经验似然估计问题.首先构造了回归系数的经验似对数似然比统计量,进一步证明了所提出的估计量渐近服从卡方分布.利用这一结果可以用来构造相应参数的置信域.
鞅差序列;部分函数线性模型;经验似然;置信域
由McGill大学的Ramsay和Bristol大学的Silverman[1]共同提出的函数型数据分析,现已被广泛应用于生物学、经济学、心理学、气象学及其他领域.考虑部分函数线性模型
(1)
式中,Y是定义在概率空间(Ω,B,P)上的相应变量;Z是取值于Rp上的可观测随机向量,并且期望值为0,二阶矩有限;X(t)是定义在(Ω,B,P)上的随机过程,E(x(t))=0,EX2(t)<∞对∀t∈T,其所有的样本函数都是T上的平方可积的函数,X(t)∈L2(T);γ(t)是T上的平方可积函数;ε是鞅差误差.为了方便起见,不妨设T=[0,1].
Ramsay和Silverman[1]在一个密集的网格均匀间隔时间点上函数预测值与反应变量的关系建模中引入函数线性模型;Cardot[2]等、Cardot[3]等、Cai和Hall[4]、Hall和Horowitz[5]、Li和Hsing[6]以及Crambes[7]等使用函数的主成分分析研究函数线性模型;Shin[8]使用主成分基函数展开以及最小二乘研究部分函数线性模型;胡玉萍[9]等使用经验似然的方法研究部分函数线性模型.
以上研究都是在考虑误差是独立的条件下进行的.然而,经济、工程、自然科学中的数据经常不是独立的,因此,鞅差作为相依情形的一种被很多学者所研究.Chen and Cui[10]使用经验似然的方法研究误差是鞅差序列的部分线性模型;Fan[11]等使用经验似然的方法研究误差是鞅差序列的Errors-in-variables部分线性模型.
考虑误差是鞅差序列的情形下函数线性模型的经验似然.构造模型(1)中参数β的经验似然比统计量,在一定条件下证明该统计量具有渐近χ2分布,并利用所得结果构造参数的置信域.
1 方法与主要结果

(2)
随机误差{εi}是关于一个增序列σ-域{Fi}的一个鞅差序列;即εi是Fi-可测的且E(εi|Fi-1)=0.符号·,·和‖·‖分别表示L2[0,1]空间的内积和范数,用KX表示随机过程X(t)的协方差函数,若KX在T×T上连续,使用Mercer's定理可以证明
式中,(λi,φi)是协方差算子KX的成对的特征值和特征函数,λ1≥λ2≥…,函数φ1,φ2,…为平方可积空间L2[0,1]的一组正交基.

式中,Y=(Y1,…,Yn)T,Z=(Z1,…,Zn)T,Um={}1≤i≤n,1≤j≤m,,γ=(γ1,…,γm)T,ε=(ε1,…,εn)T.首先假定β是已知的,由最小二乘可得γ的“伪估计”
此时可得

为了构造β的经验似然比函数,引入辅助随机变量
(3)

(4)
利用Lagrange乘子法,可得
(5)
式中,λ为Lagrange乘子,满足
(6)
为了得到R(β)的渐近分布,需要以下条件:
C1平方可积的随机函数X满足E‖X‖4<∞.
C3对特征值λj都有C-1j-a≤λj≤Cj-a,λj-λj+1≥Cj-a-1,j≥1,a≥1.


C6对于调整参数m,假定m~n1/(a+2b).

定理1 假设条件C1~C9成立,如果β是参数真值,则

根据定理1,构造β的(1-α)-水平的置信域:

2 定理的证明
引理 1 假设条件C1~C9成立,若β是参数的真值,则有
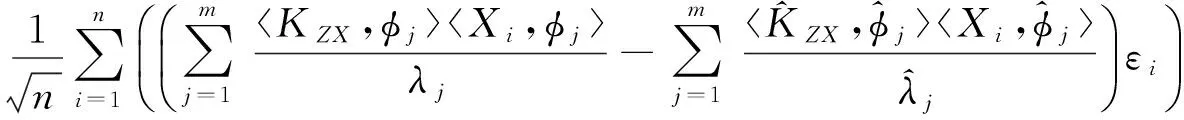
对于A2和A3,注意到E(εj)=E(E(εj|Fj-1))=0,由文献[8]中定理3.1的证明可知:
其中后面一个条件暗含了:A3=op(1).
因此,为了得到结果,只需证明


(7)
对所有的δ>0,
(8)
使用条件C4②,有
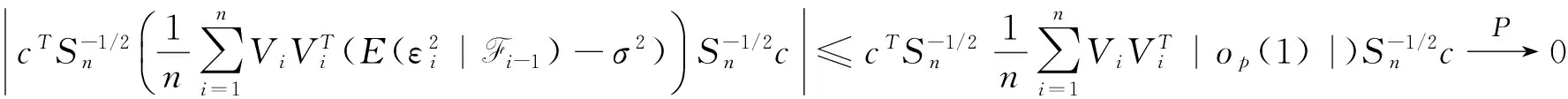
结合上式、条件C4①以及Markov不等式,对任意的δ>0,有
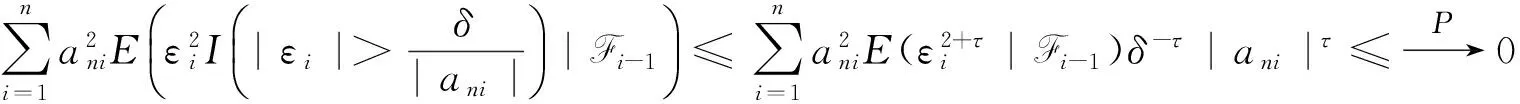
所以,可以得到式(8).引理得证.
引理2 假设条件C1~C9成立,若β是参数的真值,则有
证明:由引理1可知,


因此,
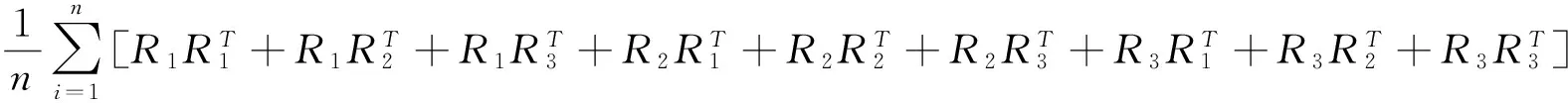
D1+D2+D3+D4+D5+D6+D7+D8+D9.
注意到B的定义以及条件C4②,对于D1,有
(9)
进一步,对于任意p-维实向量c,将证明:
(10)
这表明式(10)成立.由式(9)和式(10)有




这表明D9=Op(1).类似可证D2、D3、D4、D5、D6、D7、D8均为Op(1).综上所述,引理得证.
引理3 在定理1的条件下,若β是真实参数,则
(11)
(12)
证明:由引理2可知,
因此,有
由Shin[8]可知:
以及
结合条件C4①可得‖R1‖=op(n-1/2),‖R3‖=op(n-1/2).因此,有
利用引理2并类似于Owen的方法,可以证明式(12).
定理1的证明 对式(5)使用Taylor展开式,并且结合引理1~3,可得:
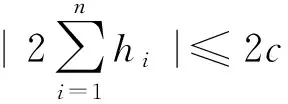
(13)
通过式(6),有:
(14)
由引理2和引理3,对于式(14)中最后一项,有
结合式(14),有
因此,使用式(13)可以得到
最后使用引理1和2完成证明.
[1] J O Ramsay,B W Silverman.Functional Data Analysis[M].New York:Springer,1997.
[2] H Cardot,F Ferraty,P Sarda.Functional Linear Model[J].Statist.Probab.Lett.,1999(45):11-22.
[3] H Cardot,F Ferraty,P Sarda.Spline Estimators for the Functional Linear Model[J].Statist.Sinica,2003(13):571-591.
[4] T T Cai,P Hall.Prediction in Functional Linear Regression[J].Ann.Statist.,2006(34):2 159-2 179.
[5] P Hall,J L Horowitz.Methodology and Convergence Rates for Functional Linear Regression[J].Ann.Statist.,2007,(35):70-91.
[6] Y Li,T Hsing.On Rates of Convergence in Functional Linear Regression[J].J.Multivariate Anal.,2007(98):1 782-1 804.
[7] C Crambes,A Kneip,P Sarda.Smoothing Splines Estimators for Functional Linear Regression[J].Ann.Statist.,2009,37:35-72.
[8] H Shin.Partial Functional Linear Regression[J].Journal of Statistical Planning and Inference,2009(139):3 405-3 418.
[9] 胡玉萍,冯三营,薛留根. 部分函数线性模型的经验似然推断[J].应用概率统计. 2015,31(2):146-157.
[10] X Chen,H J Cui.Empirical Likelihood Inference for Partial Linear Models under Martingale Difference Sequence[J].Statistics and Probability Letters,2008(78):2 895-2 901.
[11] G L Fan,H X Xu,H Y Liang.Empirical Likelihood Inference for Partially Time-varying Coefficient Errors-in-variables Models[J].Electronic Journal of Statistics,2012(6): 1 040-1 058.
Empirical Likelihood Inference for Partial Functional Linear Models under Martingale Difference Sequence
JIANG Zhi-qiang, FAN Guo-liang*
(College of Mathematics and Physics,Anhui Polytechnic University, Wuhu 241000, China)
This paper,studies the empirical likelihood estimation for partial functional linear models under martingale difference sequence.First of all,the regression coefficient of experience logarithmic likelihood ratio statistics was constructed and it was proven that the proposed estimator asymptotically obeys the chi-square distribution.The results can be used to construct the corresponding parameter confidence regions.
martingale difference sequence;partial functional linear models;empirical likelihood;confidence regions
1672-2477(2016)05-0075-06
国家统计局基金资助项目 (2015LY55)
江志强(1992-),男,安徽宿州人,硕士研究生.
范国良(1981-),男,安徽黄山人,副教授,博士.
O212.8
A

