分开是另一种美
——浅析高考压轴题中的分离变量法

广东省东莞市东莞实验中学(523120) 薛新建

分开是另一种美
——浅析高考压轴题中的分离变量法

广东省东莞市东莞实验中学(523120) 薛新建

一、问题的提出

题目(2013年新课标全国 (I)第 21题)已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.

(I)求a,b,c,d的值;

(II)若x≥-2时,f(x)≤kg(x),求k的取值范围.

本题考察函数知识,尤其是利用导数研究函数性质的一道典型题目,其中考察到了曲线与方程的关系,导数的几何意义,利用导数研究函数的单调性极值等知识.从题目结构来看,一个二次函数,一个超越函数,大多数学生拿到题目会感到既熟悉又新鲜,有一种朦胧美.解题过程集中体现了数形结合思想,分类讨论思想,函数与方程思想,转化与化归思想等数学思想.题目入手难度不大,第一问在不考虑时间以及计算失误等其他考场因素的情况下,学生基本上能够摸清思路,找到突破口,较为完整的求出4个系数,但第二问难度较大,对学生各项能力有较高的要求,需要学生在把握和坚持基本思路的基础上,按照参数对导数的符号的影响进行分类讨论,除去能力要求,还需要学生平时对此类题目有较为系统的训练和总结,才能在考场上有限时间内进行很好的处理.该题是一道区分度较为明显的经典函数题目,作为2013年理科数学全国卷的压轴题也是当之无愧.

二、解题方法探究

利用函数与导数知识可以把第(I)小题做出来,得到f(x)=x2+4x+2,g(x)=ex(2x+2).以下解答(II).

解法一设函数

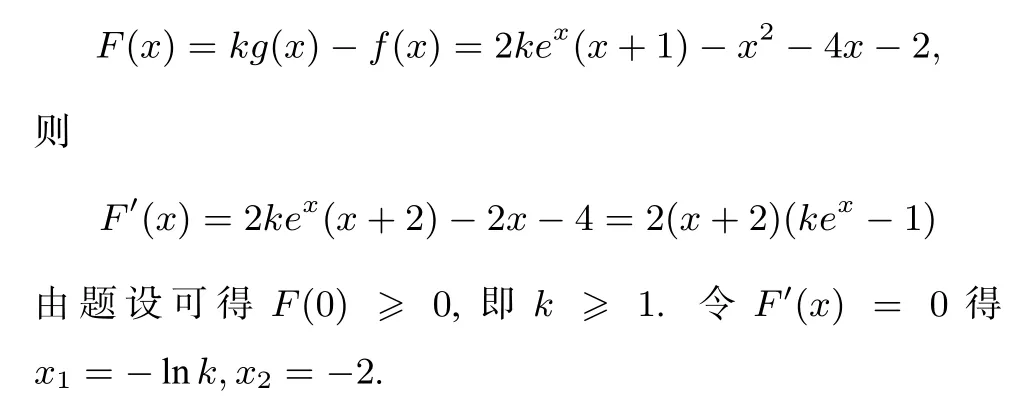
(i)若1≤k＜e2,则-2＜x1≤0.从而当x∈(-2,x1)时,F′(x)＜0;当x∈(x1,+∞)时,F′(x)＞0.即F(x)在(-2,x1)单调递减,在(x1,+∞)单调递增.故F(x)在[-2,+∞)的最小值为F(x1).而F(x1)=2x1+2-x21-4x1-2=-x1(x1+2)≥0.故当x≥-2时,F(x)≥0,即f(x)≤kg(x)恒成立.

(ii)若k=e2,则

从而当x＞-2时,F′(x)＞0,即F(x)在(-2,+∞)单调递增.而F(-2)=0,故当x≥-2时,F(x)≥0,即f(x)≤kg(x)恒成立.

(iii)若k＞e2,则

从而当x≥-2时,f(x)≤kg(x)不可能恒成立.

综上,k的取值范围是[1,e2].

解法二由题意,x≥-2时,

恒成立,(i)当x=-1时,(∗)式可化为-1≤0,恒成立.

(ii)当-2≤x＜-1时,(∗)式可化为

则y=φ(x)在[-2,-1)上单调递增,所以φmin=φ(-2)=e2,故k≤φmin=e2.

(iii)当x＞-1时,(∗)式可化为

易见y=φ(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,从而y=φ(x)在x=0处有极大值,也是最大值.所以φmax=φ(0)=1,故k≥1.

综上,k的取值范围是[1,e2].

上述方法一,采用的是构造单一函数解决恒成立问题的基本思路,这种思路容易被一般学生接受和使用,其难点在于后面的运算和对导数符号的讨论.原因是参数k的存在,造成了导数符号的不确定性.大部分学生对于带参数的求导结果的讨论会知难而退,只有少部分优秀学生能够耐下心来对后面的导函数进行分类讨论并得到正确答案.因此这种方法对学生本身素质要求过高.而且在一开始由F(0)≥0得到k≥1这一步是利用特殊点得到的k的取值范围,结论的取得有比较大的随机性,需要学生具备丰富的解题经验和在考场上的应变能力,或者说更多的是一种运气成分.

而方法二,采用的是用分离变量法解决恒成立问题的基本思路,这种思路在平时的练习题里应该经常碰到,所以对大部分学生来讲并不陌生.纵观方法二的整个过程,讨论标准就是在分离变量的过程中,(x+1)这个因式符号的正负对不等号开口方向的影响,这一点对学生素质并无太高要求,只要平时有过相关练习就可以轻易完成整个过程,而构造出来的函数y=φ(x)的单调性和最值可以通过求导进行很好的考察.通过对变量k和x的分离,避开了对含参因式的分辨,以及主次变量的讨论,将问题转化成了给定函数求最值的问题,从而降低了题目难度层次,解决起来更加容易.

将两种方法进行比较的话,方法一经典大气,但不免高冷,让人难以接近.方法二通过将变量分开,将含参导函数符号的讨论这种疑难问题轻易转化成了给定函数求最值的问题,给人一种拨云见日,曲径通幽的感觉,当然,这种分离转化本身就是数学的另一种美!

三、高考同类题目规律探寻

本题考查的函数知识点都是近年全国I卷重点考查的内容,通过对近几年函数压轴题的对比分析可以发现很多共性的地方,具体如下：①不等式恒成立求参数范围的问题,在2010-2013年连续4年考查,2014年则是证明不等式恒成立,2015年稍有变化考查函数零点分布的问题.②2011年在函数题目的设置上,第一问考查曲线与方程关系以及曲线的切线方程的问题,第二问再考查不等式恒成立问题.这样设置题目的好处就是,第一问入手门槛降低,不会在第一问就将大多数学生拒之门外,避免了出现废题的情况,第二问再考查学生能力,题目区分度较高.于是在之后的2013-2015年函数题目的布局都采用了这一方式,第一问考查切线问题似乎已成惯例.③通过对2013-2015年高考题解法的研究,不难发现分离变量法作为数学中的一种通性通法,在解决函数问题中的巨大作用,通过对字母的分离,避开主次变量间的干扰,降低问题难度的层次,体现了数学上转化与化归的思想以及正难则转的智慧.下面我们会把分离变量法在2014和2015年高考题目中的巨大作用进行展示

四、近年高考函数题的多题一解

例1 (2014年新课标全国I卷)设函数f(x)=aexlnx+曲线y=f(x)在点(1,f(1))处的切线为y=e(x-1)+2.(I)求a,b;(II)证明：f(x)＞1.

解：(I)利用导数知识可以得到a=1,b=2.

(II)由(I)知,

(I)当a为何值时,x轴为曲线y=f(x)的切线;

(II)用min{m,n}表示m,n中的最小值,设函数h(x)= min{f(x),g(x)}(x＞0),讨论h(x)零点的个数.

解：(I)略;(II)当x∈(1,+∞)时,g(x)=-lnx＜0,从而h(x)=min{f(x),g(x)}≤g(x)＜0,故h(x)在(1,+∞)无零点.

当x=1时,若min{f(1),g(1)}=g(1)=0,故x=1是h(x)的零点;若则f(1)＜0,h(1)=min{f(1),g(1)}=f(1)＜0,故x=1不是h(x)的零点.

当x∈(0,1)时,g(x)=-lnx＞0,所以只需要考虑f(x)在(0,1)的零点个数.令得,则

图1

思路分析本题关键就是求y=f(x)在(0,1)上的零点个数,而y=f(x)由于有字母a的干扰,导函数需要进行讨论,这种讨论对学生能力有较高要求.通过对a和x两个变量的分离,得到然后构造两个函数y=a和将问题转化成这两个简单函数的交点个数的问题,通过对y=φ(x)求导分析单调性,很容易就得到正确结论.

通过上述对2013-2015年的高考函数压轴题的分析,我们不难发现,分离变量法作为解决函数问题的一个基本思想方法,在高考实战中有着巨大的战略意义,那就是可以将含参问题的讨论转化成简单函数求最值的问题,对题目难度进行大幅拉低,使得更多学生具备了拿下函数压轴题的可能性,所以在以后的教学中应该特别注意强化落实这一方法.

五、变式探究

对2013年高考函数题的变式训练主要可以做如下思考：

第一类是恒成立问题变成存在性问题,因为这两类问题其实是共生的,可以做如下变式训练：

变式一已知函数f(x)=x2+ax+b,g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.

(I)求a,b,c,d的值;

(II)若∃x0∈(-1,+∞)使得f(x0)≥-kg(x0),求k的取值范围.

第二类是恒成立问题变成方程的根的分布问题,可以做如下变式训练：

变式二已知函数

若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.

(I)求a,b,c,d的值;

(II)若x∈(-1,+∞),讨论方程f(x)=kg(x)的根的个数.

当然还可以对不同类型的函数进行搭配,进行相应的变式训练.

六、高考备考策略分析

从前述分析来看,以后函数大题的高考备考需要注意以下两个方面：

1.从知识点来讲,首先要特别注意切线问题的备考,确保以后切线问题在压轴题出现的时候,学生能够得到相应分数(主要是第一问),这一部分是通过扎实备考完全可以拿下的,其次是恒成立问题求参数范围的题型的备考,要注重基本思路基本方法的普及,为优秀学生拿下压轴题打好基础,即便不能完全拿下,也可以尽量分步得分.

2.从思想方法来讲,函数部分的备考要特别注意分离变量法这一方法,前面已经展示了这一方法在近三年高考压轴题中转化函数问题时的巨大作用,而这一方法不止针对恒成立问题,在很多问题中都能找到它的影子,例如,不等式恒成立问题和存在性问题,零点存在性及分布问题,方程有解及根的分布问题,分式函数求最值(基本不等式)问题等等.分离变量的形式也是比较灵活,可以完全分离也可以不完全分离.而且分离变量法在高等数学里也有较大用处,比如解微分方程等.