基于优化观测矩阵的共轭梯度改进算法
兰明然,王友国,郑丹青
(南京邮电大学 理学院,江苏 南京 210046)
基于优化观测矩阵的共轭梯度改进算法
兰明然,王友国,郑丹青
(南京邮电大学 理学院,江苏 南京 210046)
测量矩阵的设计和信号的重构是压缩感知理论研究的核心问题。基于梯度下降法的QR分解观测矩阵优化使得信号在观测过程中的主要信息得以保存,而共轭梯度法则在信号的重构性能方面较理想。为此,将观测矩阵优化引入到共轭梯度重构算法中,针对共轭梯度重构算法,基于梯度下降法的QR分解优化观测矩阵,得到一个新的重构算法,即基于优化观测矩阵的共轭梯度算法。改进的算法中矩阵具有较大的列独立性以及与稀疏矩阵间相关性较低的特性,同时具有较好的性能。利用Matlab仿真实验来验证共轭梯度法与观测矩阵优化结合的重构算法的可行性及有效性。仿真结果表明,基于优化观测矩阵的共轭梯度算法在运行时间上缩短了2~3倍,优于其他一些重构算法。
压缩感知;观测矩阵;共轭梯度法;梯度下降法;QR分解
0 引 言
传统的奈奎斯特采样定理要求信号采样频率不低于信号带宽的两倍,这样才能不失真地实现重构。近年来,Donoho等在信号分解以及泛函分析的基础上,提出了一个全新的信号采样理论—压缩感知(Compressive Sensing,CS)[1-2]。该理论的核心思想:将采样和压缩合二为一,直接获取有用信息,再以解决优化问题的方式高概率重构原信号。其理论的信息处理方式将大幅降低信息采集量、缩短信息采集时间和节约信息存储空间。由于诸多优点,该理论从诞生开始就迅速引起各科研和实用机构的重视,并不断发展。CS理论的重点是信号的准确采样及其精确重构。因此观测矩阵的合理构造和信号重构就成为研究重点。
研究表明,性能优越的观测矩阵具有相关性较小的性质,它能够影响到信号的重构精度。文献[3-4]提出并验证了基于梯度下降法的QR分解观测矩阵优化的可行性和共轭梯度重构算法的优越性。对于文献[4]中提出的共轭梯度法,若将观测矩阵的优化引入其中,是否能够对结果有一个更优的改善。基于此问题,做如下理论分析:
观测矩阵的优化是基于梯度下降法和QR分解相结合,将其应用在经典重构算法OMP中,优化后的矩阵具有较大的列独立性以及与稀疏矩阵间相关性较低的特性,有较好的效果;而基于光滑L0范数(SL0)的共轭梯度重构算法是一种比较严谨的算法,在此重构算法中,选取的观测矩阵是跟其他重构算法相同的,其重构性能较好。
为此,将观测矩阵优化引入到共轭梯度重构算法中。通过大量仿真实验发现,在重构图像效果,综合考虑运行时间上的重构算法,基于优化观测矩阵的共轭梯度算法,并不劣于共轭梯度方法,且运行时间大大缩短两到三倍,进而验证了提出算法是可行及有效的。
1 压缩感知信号重构模型
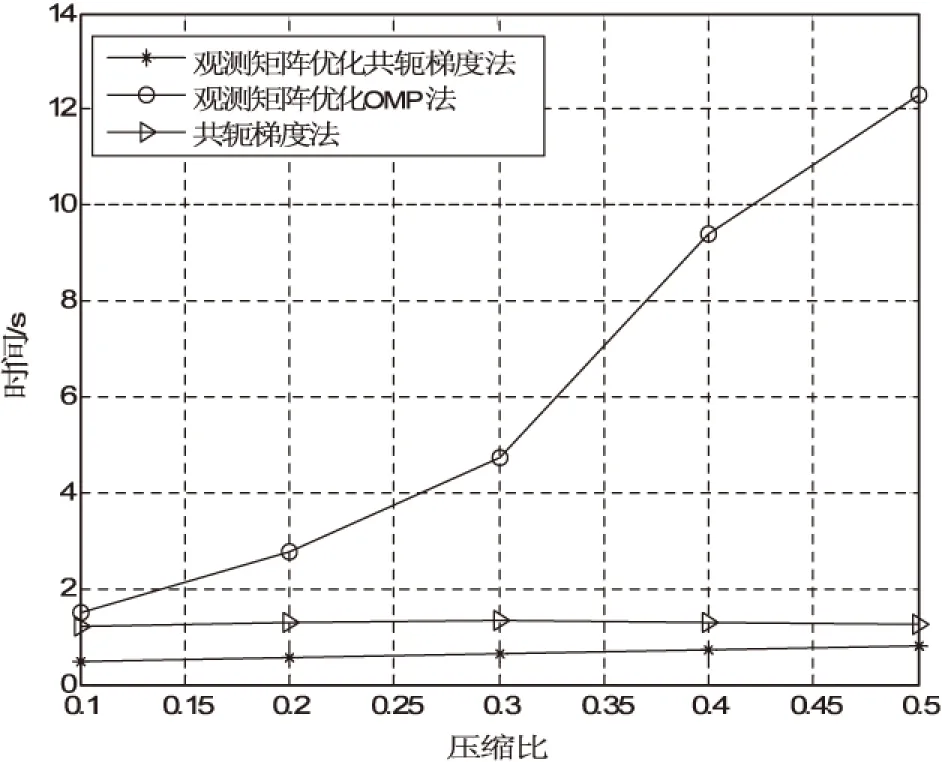
压缩感知,是给定一个可压缩或稀疏的原始信号,通过某个特定的矩阵将其投影到一个低维空间上,再利用一定的重构算法重构出原始信号[1]。CS理论的基本原理:设x为N维原始信号,稀疏度为K(即x中最多含有K个非零元素),若原始信号非稀疏,则通过稀疏矩阵对其进行稀疏化,得到信号在稀疏基下的系数Θ。观测矩阵Φ为M×N(M 从观测向量y重构出稀疏信号x的过程是解方程组的过程:y=Φx。但矩阵Φ的维数关系是M min‖x‖0 s.t.y=Φx (1) 其中,‖x‖0是向量x的l0范数,表示x中非零元素的个数。 min‖x‖1 s.t.y=Φx (2) 通常采用基追踪算法[7]或贪婪算法[8-9]。 2.1 基于梯度下降法的QR分解观测矩阵优化 该优化方法主要是以高斯矩阵为原始观测矩阵,将已有的梯度下降法与QR分解的思想相结合,得到一种新的优化方法。通过它构造Gram矩阵,利用梯度下降法对Gram矩阵逐步逼近于单位矩阵,通过迭代优化后的矩阵反向求出观测矩阵,并对其进行QR分解,得到最终优化后的观测矩阵[10-12];将最后的结果用来计算Gram矩阵,在这两矩阵反复作用的过程中,若迭代次数达到一定值时,停止迭代,输出此时的观测矩阵。具体步骤如下: 输入:稀疏矩阵Ψ,迭代步长η,最大迭代次数K 初始化:Φ为一个任意的随机矩阵,Θ=ΦΨ 对Θ做列单位化:Θ←Θ-ηΘ(ΘTΘ-I),得到:Φ1←ΘΨ-1 对Φ1进行近似QR分解优化:即先对Φ1进行QR分解,得到Φ1=QR。其中,Q为正交阵,R为上三角矩阵。然后将R中的非对角线元素设置为零,得到R1。最后根据Φ2=QR1求得进一步更新的矩阵Φ2,再根据Θ=Φ2Ψ,依次循环。 2.2 基于共轭梯度法的算法改进 s.t.y=Φx (3) 文献[13]采用最速下降法求解式(3),其搜索方向会产生“锯齿效应”,收敛速度慢。文献[14]利用修正牛顿法求解式(3),其使用的双曲正切函数fσ(xi)逼近l0范数的收敛性高于高斯函数的收敛性,但是双曲正切函数的Hesse矩阵是非正定的,文献中使用牛顿法需加入修正项,这引入了一定的“干扰”。针对这一问题,采用文献[4]提出的共轭梯度法求解式(3)。其重构算法不需要计算Hesse矩阵,进而不会引入一定的“干扰”,该方法当前搜索方向是利用梯度值与前一搜索方向构造得到的,存储量较小。使用Fletcher-Reeves公式来构造搜索方向,采用双曲正切函数逼近l0范数,对于式(3)优化问题求解的具体步骤如下: 首先确定全自动钢印打印所需运动方式,即证件必须正确堆放在固定区域,由抓手抓住证件,而后将证件准确送到钢印机打印位置,完成后打印后退回原位,抓手将证件通过另一方向移动将证件移至证件摆放区,松开抓手,抓手原位返回继续抓住第2个证件,重复上述动作,最终 (1)初始点x(1),k=1,置迭代步数Iter。 (2)k≤Iter时,求可行下降方向:d(k)= 投影梯度法求解可行方向:d(k)=PΦd(k)。其中,PΦ=I-Φ†Φ为投影矩阵,Φ†=ΦΤ(ΦΦΤ)-1为广义逆。 x(k+1)=x(k)+μd(k) k=k+1 (3)输出最优解x*=x(k+1)。 2.3 基于优化观测矩阵的共轭梯度算法 该改进方法把基于梯度下降法的QR分解优化后的观测矩阵应用于共轭梯度重构算法中,优化后的矩阵具有较大独立性,同时与稀疏基间相关性较低,将其应用在经典重构算法OMP中具有较好的重构性能;而基于光滑L0范数(SL0)的共轭梯度重构算法比较严谨。把优化后的观测矩阵应用于共轭梯度重构算法中,得到一个新的重构算法,即基于优化观测矩阵的共轭梯度算法。具体过程:通过2.1的方法对矩阵进行优化,经过M×N的观测矩阵作用后得到M维的观测向量;再通过2.2提出的共轭梯度法改进的L0范数算法,进行信号重构。具体步骤如下: (3)输出最优解x*=x0。 为证实所提出的优化观测矩阵的共轭梯度算法相关理论的可行性和优越性,采用Matlab标准图像库中256*256的Lena图像进行仿真实验。将提出方法与优化的观测矩阵OMP算法[3]和共轭梯度算法[4]进行对比,在M/N<0.5范围内进行研究。分别选取不同的压缩比,比较采用不同重构算法得到的重构效果(用峰值信噪比表示)。因为初始矩阵的随机性,采用30次平均统计结果为最终结果。图1给出了不同压缩比下三种重构算法对Lena图像的重构时间。 图1 不同压缩比下三种重构算法的重构时间 由图1易知,提出的观测矩阵优化共轭梯度法的重构时间得到大大提升,特别当压缩比较小时,与共轭梯度法相比缩短了几倍,与观测矩阵优化OMP法相比,重构时间有明显的改善;时间的改善表明所提出的共轭梯度法与观测矩阵优化结合的算法是可行、有效的。 图2给出了在不同压缩比下三种重构算法对Lena图像的重构信噪比。 图2 不同压缩比下三种重构算法的重构信噪比 由图2可知,当压缩比小于0.4时,提出算法的峰值信噪比均大于其他两种算法的峰值信噪比,随着压缩比的增大,因原始信号的非稀疏性,得到的重构效果不是很理想。 图3给出了压缩比为0.4时三种重构算法对图像的重构效果。 由图3可以看出,改进算法的重构效果与另外两种算法相比还是有优势的,重构算法的信噪比基本持平,但运行时间却有很大的提升。 由图1和图2可知,提出算法的PSNR没有优于观测矩阵优化OMP算法和共轭梯度算法,但相比PSN并没有差很多。此方法最大的优势是在可以忽略的PSNR的差别下,重构时间有明显改善。以上分析表明,在不同的压缩比下,基于观测矩阵优化后的共轭梯度法的重构性能几乎都是三种算法中最佳的,在一定程度上体现了该方法的优越性。 图3 原始图像与三种重构算法生成图像的对比 将观测矩阵优化和共轭梯度算法改进的思想相结合,提出了基于观测矩阵优化的共轭梯度重构算法。通过实验仿真验证了该重构算法具有一定的优势,另外,算法保留了观测矩阵优化OMP算法的稳定性,使用较好性能的共轭梯度算法,而且与其他两种算法相比,在时间上大大缩短。当然,还可以将不同的重构算法运用到观测矩阵的优化中,可能会得到更佳的效果,这有待进一步的研究。 [1]DonohoD.Compressedsensing[J].IEEETransactionsonInformationTheory,2006,52(4):1289-1306. [2]CandesE.Compressivesampling[C]//Proceedingoftheinternationalcongressofmathematicians.Madrid,Spin:[s.n.],2006:1433-1452. [3] 傅迎华.可压缩传感重构算法与近似QR分解[J].计算机应用,2008,28(9):2300-2302. [4]ZhengDanqing,WangYouguo,WangLu,etal.ReconstructionalgorithmforcompressedsensingbasedonsmoothedL0normandGaussianconjugategradientmethod[J].JournalofComputationalInformationSystems,2015,16:6101-6109. [5]DonohoDL.Formostlargeunderdeterminedsystemsoflinearequations,theminimall1normsolutionisalsothesparsestsolution[J].CommunicationsonPureandAppliedMathematics,2006,59(6):797-829. [6]DonohoD,TsaigY.Extensionsofcompressedsensing[J].SignalProcessing,2006,86(3):533-548. [7]ChenSS,DonohoDL,SaundersMA.Atomicdecompositionbybasispursuit[J].SIAMJournalonScientificComputing,2001,43(1):129-159. [8]TroppJA,GilbertAC.Signalrecoveryfromrandommeasurementsviaorthogonalmatchingpursuit[J].IEEETransactionsonInformationTheory,2007,53(12):4655-4666. [9]NeedellD,VershyninR.Uniformuncertaintyprincipleandsignalrecoveryviaregularizedorthogonalmatchingpursuit[J].FoundationsofComputationalMathematics,2007,9(3):317-334. [10]CandesE,TaoT.Nearoptimalsignalrecoveryformrandomprojections:universalencodingstrategies[J].IEEETransactionsonInformationTheory,2007,52(12):5406-5425. [11]BaraniukR.Alectureoncompressivesensing[J].IEEESignalProcessingMagazine,2007,24(4):118-121. [12]DonohoDL,StarkPB.Uncertaintyprinciplesandsignalrecovery[J].SIAMJournalonAppliedMathematics,1989,49(3):906-931. [13]MohimaniH,Babaie-ZadehM,JuttenC.Afastapproachforovercompletesparsedecompositionbasedonsmoothedl0norm[J].IEEETransactionsonSignalProcessing,2009,57(1):289-301. [14] 赵瑞珍,林婉娟,李 浩,等.基于光滑l0范数和修正牛顿法的压缩感知重建算法[J].计算机辅助设计与图形学学报,2012,24(4):478-484. Improved Conjugate Gradient Algorithm Based on Optimization ofMeasurement Matrix LAN Ming-ran,WANG You-guo,ZHENG Dan-qing (College of Science,Nanjing University of Posts and Telecommunications,Nanjing 210046,China) The design of measurement matrix and the reconstruction of signal is the key in the study of compressed sensing theory.QR decomposition measurement matrix optimization based on gradient descent method makes it possible to preserve the main information during the process of observation,and the conjugate gradient algorithm is ideal for the reconstruction of the signal.The measurement matrix has been introduced to optimize the conjugate gradient reconstruction algorithm.In view of the conjugate gradient reconstruction algorithm,QR decomposition based on gradient descent method is used to optimize the measurement matrix and a new reconstruction algorithm,a conjugate gradient algorithm based on optimization of the measurement matrix,is obtained.In the improved algorithm,the matrix has larger column independence and lower correlation with sparse matrix,and has better performance with conjugate gradient method.Simulation experiments with Matlab have verified the new algorithm is feasible and effective.The results show that the conjugate gradient optimization algorithm with measurement matrix has been reduced 2~3 times in running time,which is greatly superior to other reconstruction algorithm. compressive sensing;measurement matrix;conjugate gradient method;gradient descent method;QR decomposition 2016-06-07 2016-09-21 网络出版时间:2017-03-13 国家自然科学基金资助项目(61179027) 兰明然(1992-),女,硕士研究生,研究方向为信号处理理论与应用;王友国,教授,博士生导师,研究方向为信息理论及应用、编码理论与应用、随机共振理论与研究。 http://kns.cnki.net/kcms/detail/61.1450.TP.20170313.1547.088.html TP301.6 A 1673-629X(2017)05-0073-04 10.3969/j.issn.1673-629X.2017.05.016
2 基于观测矩阵优化的重构算法的改进




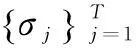
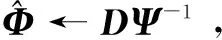

3 实验仿真与分析


4 结束语

