一类具有记忆项的双曲型方程解的能量衰减估计
熊 胤, 蒲志林
(1. 四川师范大学 法学院, 四川 成都 610066; 2. 四川师范大学 数学与软件科学学院, 四川 成都 610066)
一类具有记忆项的双曲型方程解的能量衰减估计
熊 胤1, 蒲志林2
(1. 四川师范大学 法学院, 四川 成都 610066; 2. 四川师范大学 数学与软件科学学院, 四川 成都 610066)
讨论了一类带记忆项的双曲型的阻尼波动方程解的能量衰减估计问题.此类方程的损耗十分微弱,且包含在记忆项中.利用乘子思想,构造等价于能量函数E(t)的Lyapunov函数L并利用微分不等式来得到相应的解的能量衰减估计.
波方程; 衰减估计; 记忆项; 能量等式
带有记忆项的双曲型方程由于在现代控制理论、空间技术以及材料分析等领域有许多应用[1-2],近年来受到广泛的关注.这类方程的耗散性主要是由非线性记忆项所确定,因此,耗散估计对于建立解的动力学和分析学性质有着重要的作用[3-4],其中,具有双曲型的一类偏微分方程描述了带有衰退记忆的简单粘弹性材质[5-11].
设Ω⊂R3是一个有界区域.考虑出现在等温的粘弹性理论中的如下方程
其中,g是一个非线性项,f是一个给定的与时间无关的外力,u=u(x,t)是实值函数,代表位移矢量.这种形式的方程也出现在伴随着有衰减记忆和耗散的粘弹性固体的描述中.如果k′≡0,则方程(1)转化为一个阻尼波方程[12-13].
对于这类带记忆项的双曲线型的阻尼波方程,文献[14]引入了新的变量
ηt(x,s)=u(x,t)-u(x,t-s),
对上式中的t求导得
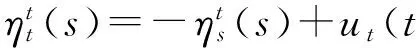
同时,令μ(s)=-k′(s)且k(∞)=1,定义v=ut,则方程(1)可以转化为如下形式
其初值边界条件为
其中
由文献[10]中的结果,将具有初值Z0=(u0,v0,η0)的系统(2)和(3)中具有唯一的解,记为S(t)Z0.对记忆项μ做如下的假设[11]:
(H1)μ∈C1(R+)∩L1(R+),∀s∈R+;
(H2)μ(s)≥0且μ′(s)≤0,∀s∈R+;
(H3)μ′(s)+δμ(s)≤0,∀s∈R+且δgt;0.
同时,设g∈C1(R),定义

对非线性项进一步做如下假设[11]:存在某些C0,Ngt;0满足:
(G3) |g′(u)|≤N(1+|y|r),0≤rlt;2.
显然,有假设条件(G1)和(G2)可知[1,15]
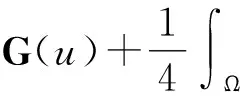
(4)
和

(5)
对某些C1,C2gt;0,其中
1 记号与引理
令Ω⊂R3是一个有光滑边界的有界区域,并且在Ω中引进空间

记V的对偶空间
V*=H-1(Ω).

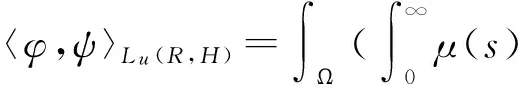
和范数

最后介绍如下的乘积Hilbert空间

引理1.1[2,18]设Φ是定义在R+上的一个非负的绝对连续函数,且若对某些εgt;0满足微分不等式
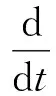
其中Λ≥0,f∈F,则以下不等式成立
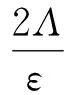
2 主要结果
方程(2)中的记忆项μ在满足条件(H1)~(H3)下,进一步对其做如下假设:

(H5) 存在s0≥0,当s≥s0,Mgt;0时满足
μ′∈L2(0,s0),μ′(s)+Mμ(s)≥0.
同时,对非线性项的假设条件也做了修改,在满足(G1)、(G2)的情况下,(G3)变为如下形式:
为了描述这个系统解的渐近行为,需要介绍定义在R+上的L2实值函数空间F,即

设

令f∈F,定义
容易得到

(6)
在t时刻与(2)式相关的能量可以表示为如下方程:


(7)

E(t)≤Ce-εtε(0)+K,
(8)
其中t≥0,f∈F.若g≡0,则K=0.
3 主要结果的证明
先引入2个泛函:

(9)

(10)

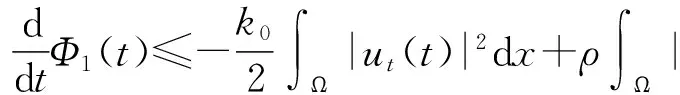
(11)
证明对Φ1(t)在t时刻求导有
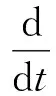
(12)
由(H2)和(H5)知
0≥μ′(s)≥-Mμ(s),
|μ′(s)|=-μ′(s)≤Mμ(s),
且对∀s∈(0,s0),由μ(s)≥0,μ′(s)≤0可知
此外,对X1=(x1(t),y1(t),u1(t),v1(t))T,Y1=(p1(t),q1(t),w1(t),z1(t))T有
所以有

(13)
又可知

(14)
由上面得到的结果,再对等式(12)右边的第一项进行估计得
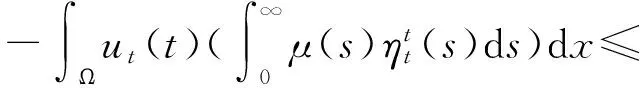
(15)
这里的C3包含k0、μ(s0)、M.
接下来,将(2)式代入等式(12)右边第二项得

(16)
再对(16)式等号右边的4项分别进行估计

(17)

(18)
|g(u)|≤|g(0)|+T|u|,

(19)

(20)

(21)
其中,C4、C5、C6都是非负常数,且如果g≡0,则C6=0.

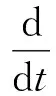
(22)
证明对Φ2(t)在t时刻求导并将(2)式代入得
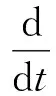
(23)
再对(23)式右边各项进行必要的估计:
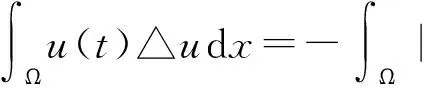
(24)

(25)
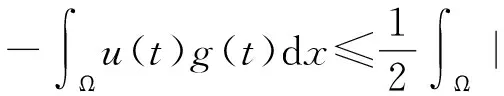
(26)
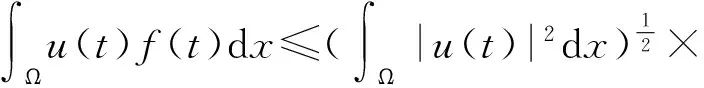
(27)
综合上面的估计,可以从(23)式得到
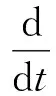
(28)
对于方程

用ut作乘子,在Ω上积分,得到如下等式
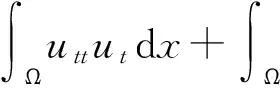
对(7)在t时刻求导,可得

又因为
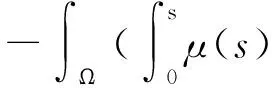
所以有

即
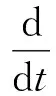
(29)
对(29)式等号右边两项分别进行估计,得到

(30)
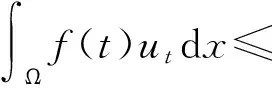
所以,可以得到如下估计:
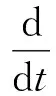
(32)
为了得到想要的结果,对于N,vgt;0,构造如下形式的Lyapunov泛函:
L(t)=NE(t)+NG(u(t))+NC1+Φ1+vΦ2,
对L(t)在t时刻求导,并根据(21)、(28)和(32)式得到的结果有
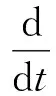

(33)

(34)
首先,由(4)和(5)式可得
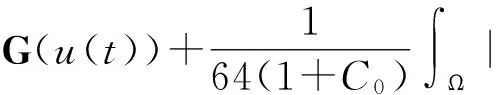
(35)
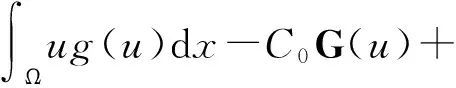
(36)
其中,某些C1,C2gt;0,则

(37)
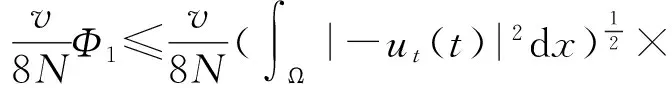
(38)

(39)
由上面三项估计得到的结果可知
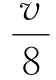
(40)

综合以上估计的结果,可得

(41)
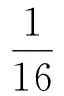

再取足够小的v和足够大的N,满足




(42)
易知存在C7gt;0,使得
(43)
从而得到想要的结果
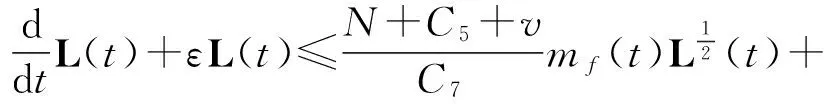
(44)
再利用引理1.1可得

(45)
再次根据(44)式得到关于E(t)的不等式

即
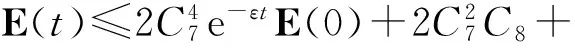
令
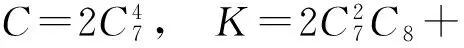
最终可得
E(t)≤Ce-εtE(0)+K.
(46)
当Φ=0(F=0),g≡0时,Φ2=0,则定理2.1得证.
[1] GHIDAGLIA J M, TEMAM R. Attractors for damped nonlinear hyperbolic equations[J]. J Math Pures Appl,1987,66(3):273-319.
[2] HARAUX A. Systèmes Dynamiques Dissipatifs et Applications[M]. Paris:Masson,1991.
[3] PATA V, PROUSE G, VISHIK M I. Traveling wave of dissipative non-autonomous hyperbolic equations in a strip[J]. Adv Diff Eqns,1998,3(2):249-270.
[4] CONTI M, PATA V. Weakly dissipative semilinear equations of viscoelasticity[J]. Commun Pure Appl Anal,2005,4(4):705-720.
[5] GATTI S, PATA V, ZELIK S. A Gronwall-type lemma with parameter and disspative estimates for PDEs[J]. Nonlinear Anal,2009,70:2337-2343.
[6] FABRIZIO M, MORRO A. Mathematical problems in linear viscoelasticity[C]//SIAM Studies in Applied Mathematics. Philadelphia:SIAM,1992.
[7] RENARDY M, HRUSA W J, NOHEL J A. Mathematical problems in viscoelasticity[C]//Pitman Monographs and Surveys in Pure and Applied Mathematics, 35. New York:Wiley,1987.
[8] COLEMAN B D, NOLL W. Foundations of linear viscoelasticity[J]. Rev Mod Phys,1961,33(2):239-249.
[9] DAFERMOS C M. Asymptotic stability in viscoelasticity[J]. Arch Rational Mech Anal,1970,37(4):297-308.
[10] PATA V, ZUCCHI A. Attractors for a damped hyperbolic equation with linear memory[J]. Adv Math Sci Appl,2001,2:505-529.
[11] PATA V. Exponential stability in linear viscoelasticity[J]. Quart Appl Math,2006,64:499-513.
[12] HARAUX A. Two remarks on dissipative hyperbolic problems[C]//Lions J L. Seminaire du College de France. Boston:Pitman,1985.
[13] HALE J K. Asymptotic Behaviour of Dissipative Systems[M]. Providence RI:Am Math Soc,1988.
[14] PATA V. Uniform estimates of Gronwall type[J]. J Math Anal Appl,2011,373(1):264-270.
[15] GIORGI C, MARZOCCHI A, PATA V. Asymptotic behavior of a semilinear problem in heat conduction with memory[J]. Nonlinear Differential Equations Appl,1998,5(3):333-354.
[16] TEMAM R. Infinite-dimensional Dynamical Systems in Mechanics and Physics[M]. New York:Springer-Verlag,1988.
[17] GIORGI C, MUNOZ RIVERA J E, PATA V. Global attractors for a semilinear hyperbolic equation in viscoelasticity[J]. J Math Anal Appl,2001,260(1):83-99.
[18] BREZIS H. Operateurs Maximaux Monotones[M]. Amsterdam:North-Holland,1973.
[19] DAFERMOS C M. Contraction semigroups and trend to equilibrium in continuum mechanics[C]//Applications of Methods of Functional Analysis to Problems in Mechanics. Lecture Notes in Mathematics,503. Berlin, New York:Springer-Verlag,1976:295-306.
[20] LIU Z, PENG C. Exponential stability of a viscoelastic Timoshenko beam[J]. Adv Math Sci Appl,1998,8(1):343-351.
[21] LIU Z, ZHENG S. Exponential stability of the Kirchhoff plate with thermal or viscoelastic damping[J]. Quart Appl Math,1997,55:551-564.
[22] LIU Z, ZHENG S. On the exponential stability of linear viscoelasticity and thermoviscoelasticity[J]. Quart Appl Math,1996,54:21-31.
[23] FABRIZIO M, LAZZARI B. On the existence and asymototic stability of solutions for linear viscoelastic solids[J]. Arch Rational Mech Anal,1991,116:139-152.
[24] CHEPYZHOV V V, PATA V. Some remarks on stability of semigroups arising from linear viscoelasticity[J]. Asymptot Anal,2006,46:251-273.
[25] BABIN A V, VISHIK M I. Attractors of Evolution Equations[M]. Amsterdam:North-Holland,1992.
[26] CHEPYZHOV V V, VISHIK M I. Attractors of non-autonomous dynamical systems and their dimension[J]. J Math Pure Appl,1994,73:165-190.
[27] GIORGI C, NASO M G, PATA V. Exponential stability in linear heat conduction with memory:a semigroup approach[J]. Commun Appl Anal,2001,5(1):121-134.
[28] DAFERMOS C M. On abstract Volterra equations with applications to linear viscoelasticity[J]. J Diff Eqns,1970,7(3):554-569.
2010MSC:35B40
(编辑 周 俊)
Decay Estimate of Energy for the Solution of Hyperbolic Equation with Memory
XIONG Yin1, PU Zhilin2
(1.CollegeofLaw,SichuanNormalUniversity,Chengdu610066,Sichuan;2.CollegeofMathematicsandSoftwareScience,SichuanNormalUniversity,Chengdu610066,Sichuan)
In this paper, we discuss the energy attenuation estimation problem for a class of hyperbolic damped wave equations with memory terms.The loss of such equations is very weak and is included in the memory terms. We use the idea of multipliers to construct a function that is equivalent to the energy of systemE(t) of a Lyapunov functionL(t) and obtain the energy attenuation estimation of the corresponding solution by using the differential inequality.
wave equation; decay estimate; memory kernel; energy equation
O175
A
1001-8395(2017)06-0760-08
10.3969/j.issn.1001-8395.2017.06.009
2017-02-27
四川省科技计划项目(2015JY0125)
熊 胤(1989—),男,助教,主要从事偏微分方程理论的研究,E-mail:xy697xy@sina.com

