一类具有免疫反应和抗逆转录病毒治疗的HIV病毒传染病模型的动力学性态分析*

李桂花， 张彩霞

(中北大学 理学院， 山西 太原 030051)

一类具有免疫反应和抗逆转录病毒治疗的HIV病毒传染病模型的动力学性态分析*

李桂花， 张彩霞

(中北大学 理学院， 山西 太原 030051)

研究了一类具有免疫反应和抗逆转录病毒治疗的HIV病毒传染病模型的动力学性态. 通过理论分析, 给出疾病发生的基本再生数R0： 当R0<1时, 系统只存在无病平衡点, 且是局部渐近稳定的； 当R0>1时, 系统存在惟一的正平衡点, 且是局部渐近稳定的. 通过数值模拟发现， 当R0<1时, 无病平衡点是全局渐近稳定的， 即疾病消失； 当R0>1时, 正平衡点是全局渐近稳定的， 即疾病流行. 通过分析发现CTL细胞免疫反应的有效率越高, CD4+T细胞被再次感染的概率越低, 即HIV患者的免疫力提高, 有效地控制了疾病的传播.

传染病模型; CTL细胞; 免疫反应; 抗逆转录病毒治疗; HIV病毒

获得性免疫缺陷综合症是艾滋病病毒(HIV)的全称， 它是由人类免疫缺陷病毒的逆转录病毒感染后， 使患者的免疫系统遭到破坏， 进而成为许多伺机性疾病的攻击目标， 形成多种临床症状， 统称为综合症， 并不是单纯的一种疾病. 在医学研究方面， 对于HIV病毒的治疗， 通常采用逆转录酶抑制剂(NNRTIs)和蛋白酶抑制剂(PIs)， 这两种治疗方式都能有效控制HIV病毒的传播. 1994年由何大一提出了“鸡尾酒疗法”， 即抗逆转录病毒治疗(ART)， 它是把逆转录酶抑制剂和蛋白酶抑制剂高效结合， 这种治疗方式既抑制了单一药物的耐药性， 又能有效地控制疾病的传播[1]. 虽然“鸡尾酒疗法”不能完全治愈艾滋病， 但目前它是阻断艾滋病进攻的最有效方法. 为此， 许多学者对HIV病毒建立不同的数学模型进行动力学研究[2-13].

(1)

然而， 由于以上治疗药物价格昂贵， 毒副作用大等， 影响了抗病毒治疗的疗效， 因此， 安全有效的治疗方式成为控制HIV病毒传播的首选. 生物学上， 特异性的细胞毒性T淋巴细胞(CTL)在控制病毒复制中发挥着重要的作用. CTL可以通过分泌各种细胞因子杀死感染的靶细胞， 还可以通过某些化学反应趋化因子来抑制HIV病毒的繁殖.

综合以上分析， 结合“鸡尾酒疗法”和CTL免疫反应， 将T细胞分为健康的T细胞(T)和被感染的T细胞(T*)， 将病毒分为具有传染性的病毒粒子 (VI) 和不具有传染性 的病毒粒子 (VNI);L表示CTL反应. 本文假设CTL细胞是以常数输入率增加的， 健康的T细胞和被感染的T细胞分别以不同的速率进行有丝分裂增殖， 于是建立如下动力学模型

(2)

式中：s为由胸腺产生的T细胞的常数输入率;α，β和ε分别为健康细胞、 被感染细胞和病毒粒子的死亡率;r1和r2分别为健康细胞和被感染细胞的自身有丝分裂的增殖率; 从生物学角度来说， 健康细胞的自身增殖率比被感染细胞的自身增值率要大， 而死亡率比被感染细胞的死亡率要小， 即r1>r2，α<β; 1-σ1和1-σ2分别为RTIs和PIs药物治疗的有效率;c为CTL细胞的输入率;b为CTL细胞的死亡率;k为一个病毒粒子感染一个健康细胞的传染率;N为一个被感染细胞死亡后裂解为病毒粒子的裂解量;p为CTL细胞免疫反应的有效率;Tm为人体内细胞的最大浓度.

由于模型(2)中的第5个方程与其他4个方程是独立的， 所以模型(2)可化为以下系统

(3)

本文将对系统平衡点的存在性、 平衡点的局部稳定性进行分析， 并对其进行数值模拟.

1 平衡点的存在性

当人体内没有HIV病毒时， 体内的CD4+T细胞动力学性态可由如下关系式表达

令以上方程的右端为零， 可得

从系统(3)得知,

由α≤β，r1≥r2， 有lim supt→∞T(t)+T*(t)≤T0， 即对任意t≥0， 有T(t)+T*(t)≤T0. 由于T*是有界的， 且由系统(3)的第3个方程可知，VI(t)是有界的， 则存在常数M>0， 使VI(t)≤M.

由此可知， 系统(3)的可行域为

令系统(3)的等式右端都为零， 即

将式(6)代入方程组(5)的第2个式子得

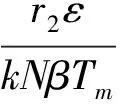
将式(6)和式(8)代入方程组(5)的第1个式子得

s=(A+BVI)(C+DVI),

其中:

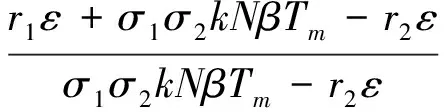
利用 van den Driessche 和 Watmough的方法[14]， 计算系统(3)的基本再生数

则

FV-1=

根据文献[14]可得系统(3)的基本再生数为

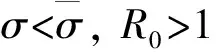
下面对正平衡点的存在性分3种情况进行讨论:

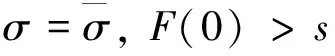
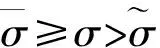
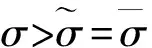
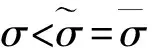
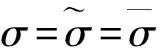
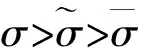
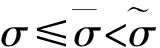
通过以上分析， 得到如下定理:

定理1 对于系统(3)， 无病平衡点P0始终存在. 当R0≤1时， 不存在正平衡点; 当R0>1时， 存在惟一的正平衡点P*.

2 平衡点的稳定性

系统(3)在无病平衡点P0的Jacobian矩阵为

显然， 矩阵J(P0)有两个负特征根， 分别为

则剩余两个特征根满足如下多项式

λ2-tr(J)λ+det(J)=0,

其中

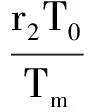
显然， 要想使J(P0)的特征根都为负， 则必须满足det(J)>0， 则R0<1. 通过以上分析， 可得如下定理:

定理2 当R0<1时， 系统(3)的无病平衡点P0是局部渐近稳定的; 当R0≥1时，P0是不稳定的.

下面对正平衡点P*的局部稳定性进行分析.

系统(3)在正平衡点P*处的Jacobian矩阵为

显然， 矩阵J(P*)有一个负的特征根λ1=-b. 则剩余3个特征根满足

λ3+a1λ2+a2λ+a3=0，

其中:

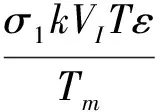
假设a1a2-a3>0, 根据 Routh-Hurwitz 判据， 可知J(P*)的所有特征根均为负. 于是有以下定理:

定理3 假设a1a2>a3， 当R0>1时， 系统(3) 的正平衡点P*是局部渐近稳定的.

3 数值模拟与讨论

本节将对系统(3)平衡点的稳定性进行数值模拟.

图 1 为系统(3)状态变量浓度随时间的变化情况， 其中固定参数r1=0.035，r2=0.025，α=0.038，β=0.04，Tm=1 500，ε=0.03，N=10，k=0.000 2，s=30，σ1=0.5，σ2=0.6，c=0.15，b=0.000 5. 图1(a)中选取p=0.006， 得R0=0.47<1； 在图1(b)中取p=0.002， 得R0=1.54>1. 由图可知， 随着时间的逐渐增加， 最终轨线都趋于稳定. 通过数值模拟发现， 当R0<1 时， 无病平衡点P0是全局渐近稳定的; 当R0>1时， 正平衡点P*是全局渐近稳定的.

图 1 系统(3)状态变量浓度随时间的变化图Fig.1 The variation of variable concentration with time in system (3)

4 结 论

[1] 利维， 邵一鸣. 艾滋病病毒与艾滋病的发病机制[M]. 北京： 科学出版社， 2000.

[2] Li J， Men K， Yang Y， et al. Dynamical analysis on a chronic hepatitis C virus infection model with immune response[J]. Journal of Theoretical Biology， 2015， 365: 337-346.

[3] Luo J， Wang W， Chen H， et al. Bifurcations of a mathematical model for HIV dynamics[J]. Journal of Mathematical Analysis and Applications， 2016， 434(1): 837-857.

[4] Zhou X， Shi X， Zhang Z， et al. Dynamical behavior of a virus dynamics model with CTL immune response[J]. Applied Mathematics and Computation， 2009， 213(2): 329-347.

[5] Wodarz D， Jansen V A A. A dynamical perspective of CTL cross-priming and regulation: implications for cancer immunology[J]. Immunology Letters， 2003， 86(3): 213-227.

[6] Wang J， Teng Z， Miao H. Global dynamics for discrete-time analog of viral infection model with nonlinear incidence and CTL immune response[J]. Advances in Difference Equations， 2016(1): 1-19.

[7] Bonhoeffer S， May R M， Shaw G M， et al. Virus dynamics and drug therapy[J]. Proceedings of the National Academy of Sciences， 1997， 94(13): 6971-6976.

[8] Perelson A S， Nelson P W. Mathematical analysis of HIV-1 dynamics in vivo[J]. SIAM Review， 1999， 41(1): 3-44.

[9] Perelson A S， Neumann A U， Markowitz M， et al. HIV-1 dynamics in vivo: virion clearance rate， infected cell life-span， and viral generation time[J]. Science， 1996， 271(5255): 1582.

[10] Wang L， Li M Y. Mathematical analysis of the global dynamics of a model for HIV infection of CD4+T cells[J]. Mathematical Biosciences， 2006， 200(1): 44-57.

[11] Wang L， Ellermeyer S F. HIV infection and CD4+T cell dynamics[J]. Discrete and Continuous Dynamical Systems-Series, 2006(6): 1417-1430.

[12] Nowak M， May R M. Virus dynamics: mathematical principles of immunology and virology: mathematical principles of immunology and virology[M]. Oxford: Oxford University Press， 2000.

[13] Li M Y， Wang L. Backward bifurcation in a mathematical model for HIV infection in vivo with anti-retroviral treatment[J]. Nonlinear Analysis Real World Applications， 2014， 17(1): 147-160.

[14] Van d D P， Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission[J]. Mathematical Biosciences， 2002， 180(1): 29-48.

AnEpidemicModelAnalysisofHIVViruswithImmuneResponseandAnti-RetroviralTreatment

LI Gui-hua, ZHANG Cai-xia

(School of Science， North University of China， Taiyuan 030051， China)

The dynamical behavior of an epidemic model for HIV with immune response and anti-retroviral treatment was studied. By theoretical analysis, the basic regeneration numberR0of disease was given. There only exists infected-free equilibrium for the model and it is locally asymptotically stable whenR0<1. And a unique positive equilibrium also locally asymptotically stable whenR0>1. By numerical simulation, it is found that the infected-free equilibrium is global asymptotically stable whenR0<1, which means that the disease will disappear. The positive equilibrium is global asymptotically stable whenR0>1, i.e., the disease will persist. By analysis, it is found that the effective rate of CTL immune response is higher, the probability of re-infection for CD4+T cells is lower. And the immunity of HIV patients is improved, the spread of virus is controlled effectively.

epidemic model; CTL cell; immune response; anti-retroviral treatment; HIV virus

1673-3193(2017)03-0255-05

O175.1

A

10.3969/j.issn.1673-3193.2017.03.001

2016-09-03

国家自然科学基金资助项目(11201434)； 山西省回国留学人员科研资助项目(2013-087)； 山西省留学回国人员科技活动择优资助项目

李桂花(1973-)， 女， 副教授， 硕士生导师， 主要从事应用数学的研究.