随机多比特翻转算法求解布尔多项式方程组可满足性问题

吕逸杰， 刘芳， 周婷， 艾江俊， 巫光福

（江西理工大学信息工程学院，江西 赣州341000）

0 引 言

低密度奇偶校验码[1]（Low Density Parity Check，LDPC）是Gallager在1962年提出的一类可以用稀疏奇偶校验矩阵或二分图定义的线性分组码，在迭代置信传播译码下具有逼近香农限[2]的良好译码性能，而且译码复杂度较低、结构灵活.由于具有良好的性能和硬件可实现性，近年来得到了广泛的关注，是4G移动通信、光纤通信、卫星数字视频广播等领域首选的编码方案[3-4].目前对LDPC码的译码算法，主要有两大类：一类是置信传播（Belief Propagation）迭代译码算法，简称BP算法[5]，该算法是基于概率的软判决译码方法，实现复杂度较高.另一类是BF（Bit Flipping）译码算法[6]，该算法是基于校验和迭代的硬判决译码方法，每次可迭代翻转多个比特，每一轮迭代是校验节点的值重新被估计，所得的值记为该校验节点的估计值.如果估计值与变量节点相连接的校验节点中，估计值不为0的个数大于估计值为0的个数，则该变量节点就会被翻转，即0变为1，1变为0.BF算法只涉及逻辑运算，简单快速且易于硬件实现，可以在译码性能和实现复杂度之间进行有效折中.目前提出了多种有效的改进方案，如加权的BF算法（WBF）及其改进形式[7-10]、引入“环检测”和比特翻转约束机制[11-12]、利用信道输出序列幅度改进结构化LDPC码[13-15]等，使其译码性能逐步接近性能较优的BP算法，但同时也加大了算法的复杂度.

布尔多项式[16-18]（Boole Polynomials)是十九世纪英国数学家乔治布尔最先提出的一种多项式，布尔多项式方程组求解问题[19-20]是数学与计算机科学中的难解之一.数学与计算机科学领域最基本的问题是一般布尔多项式方程组求解问题 （PoSSo问题），即给定一组布尔多项式，寻找变量赋值使得这些多项式取值均为0.极大布尔多项式方程组可满足性问题（Max-PoSSo问题[16]）是一般布尔多项式方程组求解问题的扩展问题，它是一类NP难问题[21]，该问题在密码学的概率代数攻击与侧信道代数攻击中广泛出现.在密码分析中的代数攻击者首先将秘密信息（如密钥）设为变量[22]，之后通过已知信息与秘密信息的关系建立相应的多项式方程组，最终通过求解多项式方程组来恢复秘密信息.然而，在多项式方程组的建立过程中，一些概率假设以及通过物理手段获取信息中出现的噪声，会造成需要求解的多项式方程组的某些项（一般为常数项）出现一定的错误，造成多项式方程组的取值无法同时为0.此时，为了恢复秘密信息，攻击者需要寻找使得方程成立个数最多的解，而该组变量有很大概率就是未出现错误的方程组的解.

目前已知的对极大布尔多项式方程组可满足性问题求解的思路不多，主要的思路有两类：一类是遍历变量取值，此类方法的思想是通过遍历变量取值并结合一些减少搜索分支策略来寻找最优的变量赋值，主要利用一些代数变换，将Max-PoSSo问题转化为一些有成熟求解算法的问题，此时，需要研究的是如何有效地将Max-PoSSo转化为其他问题，使得求解效率更高.另一类是遍历多项式取值，固定每个多项式的取值，求解对应的一般布尔多项式方程组，若能找到使得对应一般多项式方程组有解，且0的个数最多的多项式取值，则一般多项式方程组的解是Max-PoSSo问题的解.此时，需要研究的问题是如何将代数求解算法与搜索策略有效结合，减少搜索分支并提高单分支的求解效率.两种算法均存在不足之处，实现复杂度较大.在文献[16]中，作者提出一种基于回溯搜索多项式取值与递增求解代数系统思想的算法.较有效的算法还有Groebner基方法[23]、SAT方法、特征列方法[24].

文献[6]中提出比特翻转译码算法对LDPC码进行译码.通过对BF算法的研究可以寻找解决极大布尔多项式方程组可满足性问题.BF算法主要应用于低密度奇偶校验码问题，此类低密度奇偶校验码的译码问题与解决极大布尔多项式方程组可满足性问题极其相似，比特翻转算法可以用来求解这个极大布尔多项式方程组可满足性问题.因此，文中提出利用随机Muti-BF算法来解决极大布尔多项式方程组可满足性问题，加快搜索速度.由于并行比特翻转算法[25-34]是最简单的BF算法，与其它算法相比，该算法可以减少迭代次数，且具有很好的环检测能力，因此，文中利用LDPC码的BF算法并结合随机算法[35]提出新的算法，即随机Muti-BF算法.计算结果表明：整个方案简洁有效，实现复杂度较低，效果好、速度快，说明算法思想是高效可靠的.

1 基本描述和数学符号定义

1.1 基本描述

给定如下m个含有n个变量的布尔多项式[35]：

在 GF（2）（二元域）中寻找一组 x0，x1，…，xn-1的赋值，即每个 xi的取值均在 GF（2）中，使得 f1， f2，…，fm在这组变量赋值下取值为0的个数最多.

选取了256个含有128个变量布尔多项式，即 m=256，n=128.f1， f2，…，f256为给定的 256 个布尔多项式，但不是每个布尔多项式中都包含128个变量.

1.2 数学符号定义

假设变量 x0，x1，…，xn-1统一用 xi表示，i＝0，1，…，n-1，布尔多项式 f1， f2，…，fm统一用 fj表示，j=1,2,…,m，m=256，n=128，即：

记Sx表示包含xi的函数集合，即：

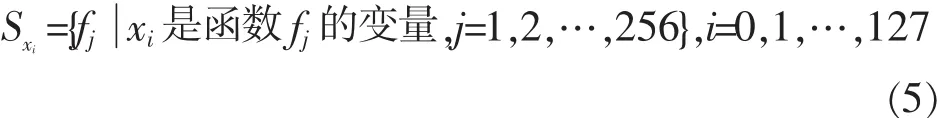
Ax表示含xi的函数值等于1的集合，即：

N为自然数，表示已知设定最大迭代次数．ri表示随机产生的0到1的一个随机数,即0＜ri＜1．

2 算法思想

2.1 BF算法简介

BF算法的核心思想是：如果某比特所参与校验式的结果数据大多数有错，则认为该比特的错误概率较大，因而将该比特进行翻转，BF算法中由于不包含非线性运算，因此复杂度低，能得到较低的误码率．

设LDPC码的校验矩阵为Hm*n，信道接收到的码序列为x→=（x0，x1，…，xn-1），接收到序列的二进制硬判决结果为J，校验结果序列为h，则：

算法流程如下:

步骤3定义集合Ω,集合Ω中比特所对应的Si是最大的．

步骤4翻转集合Ω中的比特．

重复步骤 1～4，直至所有校验方程都满足或迭代次数都达到设定的上限．

2.2 求局部最优的贪婪算法

贪婪算法（又称贪心算法）是指，在求解时总是做出在当前看来是最好的选择．也就是说，不从整体最优上加以考虑，他所做出的仅是在某种意义上的局部最优解．贪心算法不是对所有问题都能得到整体最优解，但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解．

首先计算每个函数所包含的变量数，（f1，…，f256）得到如下结果：

假定变量总数v小于一定的整数下都是能够比较快遍历所有的可能的解空间，例如小于25，即要求解空间的大小要小于225．

贪婪算法步骤如下：

1）首先选一个变量比较少的函数，例如函数f1只包含14个变量，遍历所有变量的空间，就可以得到了213个满足f1为0的解向量集合V1．

2）尽量选择不产生新变量的函数加入，或产生新变量的个数尽量少．如果没有产生新的变量则直接把得到的解集合V1验证是否使加入的函数为0，如果是则加入到新的解集合中V2．如果产生了新的变量，设新的变量个数为n1,则要把之前的解集扩展为2n1×213个，验证是否使加入的函数为0，是则加入到新的解集合V2中．

3）重复步骤2），每次只加入一个函数，使每步扩展的解集空间的个数少于最大值225，直到所有的函数都加入．如果存在使函数都为0的解，则利用该算法一定可以求出．如果没有，则中途可能就会产生没有解．提前结束循环．

2.3 随机Muti-BF算法

随机Muti-BF算法思想：变量所对应的函数值为1的函数个数大于一定值时，将该变量以函数值为1的个数与包含函数的总数之比的概率值翻转，重复此过程，直至变量值达到稳定状态．

随机Muti-BF算法流程如下：

1）给定一组变量初始解 X*=（x0，x1，…，xn-1），设定最大迭代次数为N．

2）计算集合Sx和数值

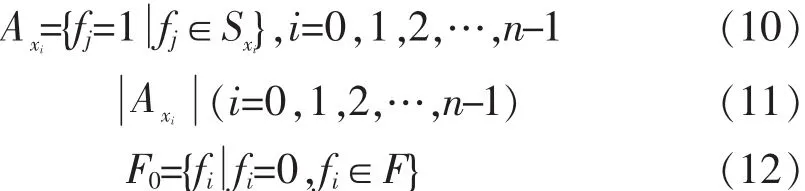
4）对 i=0，1，2，…，n-1，随机产生 0 到 1 的一个随机数 ri，若随机数，则将比特xi翻转，否则不变，最后得到的新值记为 X=（i=0，1，2，…，n-1）．

X代入步骤3），并重复步骤3～4，达到设定的迭代次数后，输出使 F0最大的一组解X及最大值F0．

3 随机Muti-BF算法的应用

将随机Muti-BF算法应用到具体例子中，变量x0，x1，…，xn-1用 xi表示，函数 f1，f2，…，fm用 fj表示，其中 m=256，n=128，即：

依次统计出布尔多项式方程组中包含变量x0，x1，…，xn-1的函数个数，即 Sxi．经过计算256个函数中，包含变量xi的函数个数 Sxi按次序分别如下：

在随机Muti-BF算法具体应用中，取N=108，每次生成128个（0,1）之间的随机数，对于xi，若函数值等于1的函数个数（即 Axi）与计算出的 Sxi之比大于等于该随机数，则将该变量的值翻转．经过几分钟的计算，得到方程组的一组最优解X=（x0，x1，…，xn-1），结果如下：

经典贪婪算法复杂度的最小估计值O（219*214）．而新的随机Muti-BF算法复杂度最大可控值是O（108），收敛的速度和随机数有关．通过与经典的贪婪算法对比可以得出，提出的新的随机Muti-BF算法在复杂度方面和搜索效果两个方面都明显更好.在随机Muti-BF算法当N到一定大的时候，就会收敛到一个最优解，因为函数变量不是线性关系，所得的解有可能不是最好的解，在什么情况下可以得到最好的解，可能与函数组变量之间的结构关系有关，值得进一步去深入研究.

4 结束语

文中利用编码理论中的译码方法，提出了一种新的求解算法思路，即结合BF算法和随机数的随机Muti-BF算法对极大布尔多项式方程组可满足性问题求解，得到了一种有效的求解算法.实验结果表明，该解决方案不仅能在二元域中高效找到一组使极大布尔多项式方程组取值为0个数最多的解，而且运算简洁快速.由于对极大布尔多项式方程组可满足性问题，现有的求解方法不是很成熟，采用编码理论中的译码方法，对译码来说，有很多个解，即变量的个数多于函数的个数，所以容易得到满足条件的解，而对于极大布尔多项式方程来说，方程的个数多于变量的个数，因此，很可能没有满足全部条件的解，如文中就没有满足全部条件的解，只能求极大可能满足的解，因此，是否存在更高效的方法来解决极大布尔多项式方程组可满足性问题值得进一步深究.

在此，文中提出一种分治法求解的思路：经过行变换与列变换将0向量移到左下角与右下角区域内，将变量 x0,x1,x2,…，x128分为 M，N两部分，如图1所示.A区域内的函数只与M部分变量有关，C区域内的函数只与N部分变量有关，B区域内的函数才与M，N两部分变量都有关，分别求3个区域的最优解，最后比较3个最优解得到整个函数的最优解.这就大大提高了求解效率.

图1 一种分治法求解的思路

[1]Marco Baldi.Low-Density parity-check codes[M].Germany:Springer International Publishing,2014:5-21.

[2]刘海盛.PS码在CMMB系统中的应用[J].中国有线电视，2009(6)：615-618.

[3]张谨，苏广川.LDPC比特翻转译码算法的分析与改进[J].计算机应用，2006，26(7)：1730-1731.

[4]张水平，林平平，王柯柯，等.二进制移位对偶码的构造[J].江西理工大学学报，2016，37(1):74-79.

[5]Mackay D J C.Good error-correcting codes based on very sparse matrices[J].IEEE Transactions on Information Theory,1999,45(2):399-432.

[6]Gallager R G.Low-Density parity-check codes[J].Ire Transactions on Information Theory,1963,8(1):21-28.

[7]Mi adinovic N,MPC Fossorier.Improved Bit-Flipping decoding of Low-Density parity-check codes[J].IEEE Transactions on Information Theory,2005,51(4):1594-1606.

[8]Roberts M K,Jayabalan R.An improved low complex hybrid weighted Bit-Flippingalgorithm forLDPC codes[J].Wireless PersonalCommunications,2015,82(1):327-339.

[9]ZhangJ,MPCFossorier.AmodifiedweightedBit-Flippingdecodingof Low-Density parity check code[J].IEEE Communnications Letters,2004,8(3):165-167.

[10]Liu Y H,Zhang M L.Modified Bit-Flipping decoding of Low-Density parity-check Codes[J].Advanced Materials Research,2013,710(7):723-726.

[11]Nouh A,Banihashemi A.Bootstrap decoding of low-density parity check codes[J].IEEE Communnications Letters,2002,6(9):391-393.

[12]Liu Z,Pados D.A decoding algorithm for finite-geometry LDPC codes[J].IEEE Transactions on Communications,2005,53(3):415-420.

[13]刘原华，张美玲.结构化LDPC码的改进比特翻转译码[J].北京邮电大学学报，2012，35(4):116-117.

[14]刘原华，张美玲.LDPC码的改进迭代比特翻转译码算法[J].电讯技术，2012，52(4):488-491.

[15]张高远，周亮，苏伟伟.基于平均幅度的LDPC码加权比特翻转译码算法[J].电子与信息学报，2013，35(11):2572-2578.

[16]Huang Z Y,Lin D D.A new method for solving polynomial systems with noise over F2 and its applications in cold boot key recovery[C]//Canada:LNCS,2013:16-33.

[17]Gao X S,Huang Z Y.Characteristic set algorithms for equation solving in finite fields[J].Journal of Symbolic Computation,2012,47(6):655-679.

[18]KimDS,KimT,SeoJ J.A note on q-analogue of boole polynomials[J].Applied Mathematics& Information Sciences,2014,9(6):3153-3158.

[19]王成龙.有限域上多项式方程组求解的三角列算法[J].中国科学院大学学报，2014，31(6):751-730.

[20]李晞.一种布尔多项式的高效计算机表示[J].计算机研究与进展，2012，49(12):2564-2574.

[21]Bard G V,Courtois N T,Jefferson C.Efficient methods for conversion and solution ofsparse systemsoflow-degree multivariate polynomia[OL].https://eprint.iacr.org/2007/024,2007-01-25.

[22]Albrecht M,Cid C.Cold boot key recovery by solving polynomial systems with noise[OL].https://martinralbrecht.files.wordpress.com/2011/06/20110607_coldboot_nerja.pdf,2011-06-07.

[23]李晞,张寅.基于ZBDD的布尔多项式Grobner基算法的实现[J].计算机应用与软件,2011,28(2):274-276.

[24]Gao X S,Huang Z.Characteristic set algorithms for equation solving in finite fields[J].Journal of Symbolic Computation,2012,47(6):655-679.

[25]Chan AM,Kschischang FR.A simple taboo based soft decision decoding alogorithm for expander codes[J].IEEE Communication Letters,1998,2(7):183-185.

[26]Lan L,Zeng L Q,Tai Y Y,et al.Construction of quasi-cyclic LDPC Codes for AWGN and binary crasure channel:a finite field approach[J].IEEE Transactions on Information Theory,2007,53(7):2429-2458.

[27]Kou Y,Lin S,Fossorier MPC.Low-density parity-check codes based on finite geometries:a radiscovery and new results[J].IEEE Transactions On Information Theory,2001,47(7):2711-2736.

[28]Jiang M,Zhao C M,Shi Z H,et al.An improvement on the modified weighted bit flipping decoding algorithm for LDPC codes[J].IEEE Communications Letters,2005,9(9):814-816.

[29]Cardarilli G C,Kaddour F,Leandri A,R,et al.Bit flip injection in processor-based architectures:a case study[J].Eighth IEEE International On-line Testing Workshop,2002:117-127.

[30]Wadayama T,Nakamura K,Yagita M,et al.Gradient descent Bit Flipping algorithms for decoding LDPC codes[J].IEEE Transactions on Communications,2010,58(6):1610-1614.

[31]Sundararajan G,Winstead C,Boutillon E.Noisy gradient descent Bit-Flip decoding for LDPC codes[J].IEEE Transactions on Communications,2014,62(10):3385-3400.

[32]Guo F,Hanzo L.Reliability ratio based weighted bit-flipping decoding for low-density parity-check codes[J].Electronics Letters,2004,40(21):1356-1358.

[33]Wu X F,Zhao C M,You X H.Parallel weighted bit-flipping decoding[J].IEEE Communications Letters,2007,11(8):671-673.

[34]Huang H,Wang Y,Wei G.Mixed modified weighted bit-flipping decodingoflow-densityparity-checkcodes[J].InternationalConference on Wireless Communications&Signal Processing,2012,9(2):1-5.

[35]Wu G F,Li Y,Zhang S P,et al.A random local matroid search algorithm to construct good rate 1/p systematic binary Quasi-Cyclic code[J].IEEE Communications Letters,2015,19(5):699-702.