On the Reliability of Double Generalized Petersen Graph∗
MA Shengdong,MENG Jixiang
(School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
0 Introduction
Throughout this paper,we consider only f i nite undirected graphs without loops or multiple edges.For notation and terminology not def i ned here,we refer the reader to[1].LetGbe a graph with vertex setV=V(G)and edge setE=E(G).For anyx∈V(G),the set{y∈V(G){x}|xy∈E(G)}is the neighborhood ofxinG,which is denoted byNG(x).The minimum degree ofGis the parameter δ(G)=min{dG(x)|x∈V(G)},wheredG(x)=|NG(x)|is the degree ofxinG.Analogously,the maximum degree Δ(G)ofGcan be def i ned.A graphGisr-regular if Δ(G)= δ(G)=r.Fore=xy∈E(G),the degree of the edgeeis def i ned as ξG(e)=d(x)+d(y)−2.The minimum edge degree of a graphGis ξ(G)=min{ξG(e)|e∈E(G)}.The path onnvertices and(n−1)edges is denoted byPn.
The connectivity κ(orλ)of a graphGis the minimum cardinality|S|of a setSof vertices(edges)whose deletion fromGresults in either a disconnected graph or a trivial graph.In this case,the setSis a vertex-cut(edge-cut)ofG.If κ= δ,then the graph is maximally connected.If λ = δ,then the graph is maximally edge connected.Harary[2]def i ned the conditional connectivity κ(G,P)as the minimum cardinality of a set of vertices,if it exists,whose deletion disconnectsGand where every remaining component has property P.This led to the study of a number of variations to the classical nation of connectivity,such as super-connectivity and super-edge-connectivity.The super-connectivity(super-edge-connectivity)of a connected graphGis the minimum number of vertices(edges)that need to be deleted fromGin order to disconnectGwithout creating isolated vertices.In the same paper,Harary also asked about the conditional connectivity of some interesting families of graphs,such as the complete multipartite graphs,the cubes,and the generalized Petersen graphs.In this work,we address his question by establishing the super-connectivity and super-edge-connectivity of the family of double generalized Petersen graphs.
Anh-connected graphGhas connectivity κ(G)≥h,for someh∈ N.A graphGis super-connected(or simply super-κ),ifGis connected and the deletion of every minimum vertex-cut yields an isolated vertex.Thus,a necessary condition for a graphGto be super-κ is thatGis maximally connected.However,the converse is not necessarily true.In general,super-vertex-cut or super-edge-cut do not always exist.The super connectivity κ1(G)(respectively,superedge-connectivity λ1(G))is the minimum cardinality over all super vertex-cuts(respectively,super-edge-cuts)inGif any,and,by convention,is+∞ otherwise.For a non-trivial graphG,if λ1(G)=ξ(G),thenGis optimal.
The generalized Petersen graphsGP[n,k](see Fig 1),f i rst introduced by Coxeter[3]in 1950,although the name was only coined in 1969 by Watkins[4],are a natural generalization of the well-known Petersen graph.

Fig 1 The double generalized Petersen graph GP[11,3]and GP[17,5]
Def i nition 1Given an integern≥3 andk∈Zn{0},2≤2k<n,the generalized Petersen graphGP(n,k)is def i ned to have vertex set{ui,vi|i∈Zn}and edge set the union Ω∪Σ∪I,where

A natural generalization of the generalized Petersen graphs are the double generalized Petersen graphsDP[n,t],which were f i rst introduced by Zhou and Feng(2012)by modifying the generalized Petersen graphs in[5].In[6],Zhou and Feng(2014)determined all non-Cayley vertex-transitive graphs and all vertex-transitive graphs among double generalized Petersen graphs.They are def i ned as follows(two examples are given in Fig 2).

Fig 2 The double generalized Petersen graph DP[5,2]and DP[8,3]
Def i nition 2Given an integern≥3 andk∈Zn{0},2≤2k<n,the double generalized Petersen graphDP[n,k]is def i ned to have vertex set{xi,yi,ui,vi|i∈Zn}and edge set the union Ω∪Σ∪I,where


In this work,it is implicitly assumed that all the subscripts of the vertices ofDP[n,k]are taken modulon.
The double generalized Petersen graphDP[n,k]is made up of an outer cycle on the outer vertices;linner cycle each of lengthon the inner vertices,since the subgraph ofGinduced by inner vertices is a bipartite graph,thustis even andt≥4;and spokes connecting an outer vertexxi,yiwith an inner vertexui,vi,wherei∈Zn(refer to Fig 2).The edges of the outer cycle are referred to as the outer edges,where as those of the inner cycle are the inner edges.In this study,the α-cycle is the inner cycle containing the vertexuα.We remark that if a vertexuiis on the α-cycle,thenvi+kandvi−kare also on the α-cycle.Ifn=3k,thenDP[n,k]haskinner cycles each of lengtht=6.
The connectivity and the super-connectivity of various families of graphs have been studied in literature,including circulant graphs[7],hypercubes(see[8]),and products of various graphs(see[9,10]).In[11],Ferrero and Hanusch establishedlowerandupper-boundsforther-componentedge-connectivityofthegeneralizedPetersengraphsGP[n,k],wheregcd(n,k)=1.In[12],BoruzanliandGaucideterminedwhenGP[n,k]aresuper-connected,superedge-connected and show that their super-connectivity and their super-edge-connectivity are both equal to four whenn∉{2k,3k}.In[13],Kutar and Petecki characterized the automorphism groups and investigated the hamiltonicity,vertex-coloring and edge-coloring properties of double generalized Petersen graph.Our result that the double generalized Petersen graphs are super-connected and super edge-connected emphasizes further their suitability for interconnection networks,even though their super-connectivity and super-edge-connectivity are not particularly high.
1 Super-connectivity of DP[n,k]
In this section,we prove that forn>kandk≥1,the graphDP[n,k]is super-connected and κ1(DP[n,k])=4,whenn∉{2k,3}.We do this by f i rst showing that providedn∉{2k,3},any vertex-cut of cardinality three isolates a vertex,then we exhibit a super vertex-cut of cardinality four which disconnectsDP[n,k]without isolating any vertex.
Lemma 1LetG=DP[n,k]forn>3 andn>k≥1.IfSis a vertex-cut ofG,thenScontains at least one outer vertex ofG.
ProofSuppose that all the vertices ofSare inner vertices ofG.InG−S,all the remaining inner vertices are adjacent to an outer vertex and each outer vertex lies on the outer cycles.Thus,G−Sis connected,a contradiction.Hence,Scontains at least one outer vertex ofG.
Inthefollowingtheoremweshowthatforn>kandk≥1,thegraphDP[n,k]issuper-connectedandκ1(DP[n,k])=4,whenn∉{2k,3};The idea behind the proof is to show that if a vertex-cutSofG=DP[n,k]has only three vertices,thenG−Sis either connected or has an isolated vertex.
Theorem 1LetG=DP[n,k]fork≥1 andn>k.The super-connectivity κ1ofGis given by
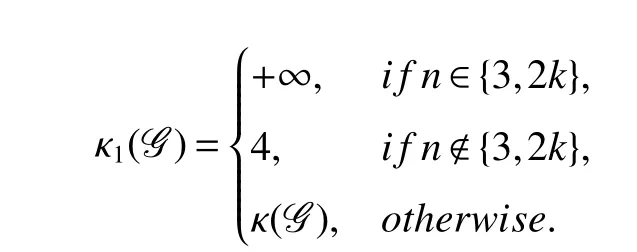
ProofItis easyto seethatDP[3,1]andDP[3,2]are notsuper-κ,since notevery vertex-cutwith cardinalitythree isolates a vertex.A possible vertex-cut with three vertices which create an isolated vertex isS={uα,xα+1,xα+2},where α∈{0,1,2}.Another kind of vertex-cut with three vertices that does not create an isolated vertex isS={u0,u1,u2}.Hence κ1(DP[3,1])= κ1(DP[3,2])=3.
In the double generalized Petersen graphDP[2k,k],the inner vertices generate a union of 2kvertex-disjoint inner edges.Since the deletion of the two outer vertices which are neighbours of the vertices joined by the same inner edge disconnectsDP[2k,k].It is easy to see that its connectivity κ(DP[2k,k])=2 and thatDP[2k,k]is not super-κ.
Letn>2kandn≠3.We suppose thatSbe a super vertex-cut such that|S|=κ1=3.Thus,G−Sis disconnected and has no isolated vertices.By Lemma 1,Scontains at least one outer vertex and we only need to consider the following three cases.
Case 1SupposeSconsists of one outer vertex and two inner vertices.In this case,all the remaining outer vertices lie on a pathPn−1or a cycleCn.
Case 1.1We suppose f i rst that these two inner vertices ofSare incident to the outer verticesxioryj,wherei,j∈ Zn.Without loss of generality,we letS={xα,uβ,uγ},then β ≠ γ.where α,β,γ ∈ {0,1,···,n−1}.
(i)we suppose f i rst that either α = β or α = γ,without loss of generality,we let α = β,then all the remaining inner vertices are joined by spokes to the outer pathPn−1and outer cycleCn,respectively.
(ii)If α ≠ β and α ≠ γ.The remaining inner vertices are all joined by spokes to the outer path and outer cycle,except foruα.IfNG−S(uα)={vα+k,vα−k},then the verticesvα+kandvα−kare joined by spokes to the outer cycleCn.Thus,there be must exist a inner vertexvτand it’s neighborsuτ+kanduτ−k,which are joined by a spoke to the outer path.Hence,in either case,G−Sis connected,contradiction.
Thus,we can assume thatS={xα,vβ,vγ},then β ≠ γ.The remaining inner vertices are all joined by spokes to the outer path and outer cycle,except foruα.IfNG(uα)={xα,vβ,vγ},thenuαis an isolated vertex inG−S,a contradiction.If not,then there is an inner vertexuτis adjacent tovα,where τ≠β or τ≠γ.In this case,the vertexuτis adjacent to an outer cycle and henceG−Sis connected,a contradiction.
Case 1.2We suppose that the two inner vertices ofSare incident to the outer vertexxβandyγ,respectively,sayS={xα,uβ,vγ},where α,β,γ ∈ {0,1,···,n−1}.Ifuα≠uβ,then all the remaining inner vertices are joined by spokes to the outer cycleCnand outer pathPn−1,a contradiction.If not,thenuα=uβ,and the remaining inner vertices are all joined by spoke to the outer cycle and outer path,excepted foruα.However,uαis adjacent to at least one of the verticesvα+kandvα−k,which is joined by a spoke to the outer cycleCn.Hence,G−Sis connected,a contradiction.
Case 2Suppose thatSconsists of two outer vertices and one inner vertexuiorvj,wherei,j∈{0,1,···,n−1}.
Case 2.1If these two outer vertices in same outer cycle,without loss of generality,we letS={xα,xβ,uγ},then α≠β,where α,β,γ ∈{0,1,···,n−1}.
If we suppose thatxαis adjacent toxβ,then all the remaining outer vertices lie on a pathPn−2and a outer cycleCn,respectively.
(i)If either γ = α or γ = β,without loss generality,we let γ = β,thenuαis adjacent to inner verticesvγ−kandvγ+kinG−Sand all the remaining inner vertices except foruγare joined by spokes to the outer pathPn−2and a outer cycle
Cn.
(ii)If γ ≠ β and α ≠ γ,then,all the inner vertices except foruβanduγare joined by spokes to the outer pathPn−2and a outer cycleCn,respectively.Since,the two inner verticesuβanduγare adjacent to the inner verticesvβ+k,vβ−k,vγ+kandvγ−kinG−S,respectively.
Hence,in either case,G−Sis connected,contradiction.
Thus,we can assume thatxαandxβare not adjacent,that is,the outer cycle is divided into two disjoint paths.Letxτbelong to the outer path,and ifNG(xτ)={xα,xβ,uγ},thenxτis an isolated vertex inG−S,a contradiction.If not,there is no common neighbor betweenxαandxβ.If the two paths are in the same component,then a similar argument to that made above implies that all the remaining inner vertices are also in the same component.ThusG−Sis connected,a contradiction.Hence,the two paths must be in two diあerent components.
Case 2.1.1We suppose that either γ = β or α = γ,without loss of generality,say α = γ.The outer vertices{xβ+1,xβ+2,···,xα−1}lie on a path and are adjacent to the inner vertices{uβ+1,uβ+2,···,uα−1}.We let these vertices be in one component,sayC1.Similarly,the vertices{xα+1,xα+2,···,xα−1,uα+1,uα+2,···,uβ−1}belong to the same component.Suppose that this is diあerent fromC1,sayC2.Also,the vertices{v0,v1,···,vn−1,y0,y1,···,yn−1}belong to the same component.Suppose that this is diあerent fromC2,sayC3.
Since every inner verticesuiinC1andC2all have two neighbor verticesvi+kandvi−kbelong toC3,wherei∈ Znandi∉ {α,β}.Thus,componentsC1,C2andC3are connected.We consider the vertexuβ,sinceNG−S(uβ)={vβ+k,vβ−k}and the verticesvβ+kandvβ−kbelong toC3.Then,all the remaining vertices ofG−Sare in the same componentC3.HenceG−Sis connected,a contradiction.
Case 2.1.2Thus γ ≠ β and α ≠ γ,without loss generality,we assume that α < γ < β.The outer vertices{xα+1,xα+2,···,xγ,···,xβ−1}lie on a path in one component,sayC1.The inner vertices{uα+1,uα+2,···,uγ−1,uγ+1,···,uβ−1}are joined by spokes toC1.Similarly,the vertices{xβ+1,···,xα−1,uβ+1,···,uα−1}belong to the same component,suppose that this is diあerent fromC1,sayC2.Also,the vertices{v0,v1,···,vn−1,y0,y1,···,yn−1}belong to the same component.Suppose that this is diあerent from bothC1andC2,sayC3.
Since all neighbors of each vertex inC1andC2,contain inC3,then,the componentC1,C2andC3are connected.In the following,we consider the inner verticesuαanduβ,sinceNG−S(uα)={vα+k,vα−k},NG−S(uβ)={vβ+k,vβ−k},and the verticesvα+k,vα−k,vβ+k,vβ−kbelong toC3,we have all the remaining vertices ofG−Sare in the same componentC3.Hence,G−Sis connected,a contradiction.
Case 2.1.3ForS={xα,xβ,vγ},where α,β,γ ∈ {0,1,···,n− 1}.If we suppose thatxαis adjacent toxβ.The remaining inner vertices,except foruαanduβare all joined by spokes to the outer pathPn−2and outer cycleCn,respectively.Assume that these vertices contain in one component,sayC.Since,NG−S(uα)={vα+k,vα−k},NG−S(uβ)={vβ+k,vα−k},then at least three vertices are belong toC.Hence,all the remaining vertices ofG−Scontain in the same component,a contradiction.Thus,we can assume thatxαandxβare not adjacent.Then,a similar argument to that made above implies that all the remaining vertices are also in the same component.Hence,G−Sis connected,a contradiction.
Case 2.2If this two outer vertices in diあerent outer cycles.Without loss of generality,we letS={xα,yβ,uγ},where α,β,γ ∈ {0,1,···,n−1}.Then,all the remaining outer vertices lie on two pathsrespectively.
(i)If α = γ,the remaining inner vertices are all joined by spokes to the outer paths,except forvβ.We consider the vertexvβ.SinceNG(vβ)={yβ,uβ−k,uβ+k},there exist at least one of the verticesuβ−koruβ+k.Which is joined by spoke to the outer pathIn the following,we consider the vertexuτ,where γ ≠ τ.SinceNG−S(uτ)={xτ,vτ+k,vτ−k},then,the two outer paths are connected.
(ii)If α ≠ γ,then a similar argument to that made above implies that all the other remaining inner vertices are joined by spokes to the outer paths,except foruβandvα.SinceNG(uα)={xα,vα−k,vα+k},NG(vβ)={yβ,uβ−k,uβ+k},andSdoes not contain any vertices of the setNG(uα),then,uαis joined byvα−kandvα+kto the outer path.Forvβ,its neighborsuβ−kanduβ+khave at least one not inS,thus,vβis connected with all remaining vertices ofG−S.
Hence,in either case,G−Sis connected,a contradiction.
Case 3Suppose thatSconsists of three outer vertices,then the inner cycles are intact inG−S.
Case 3.1We suppose f i rst that these three outer vertices lie on a same outer cycle.If,without loss of generality,we letS={xα,xβ,xγ},where α,β,γ ∈ {0,1,···,n−1},neither two of which are equal.Without loss of generality,we assume that α<β<γ.
The outer verticesxα+1,···,xβ−1all lie on a path inG−Sand are adjacent to the corresponding inner verticesuα+1,···,uβ−1.Thus,they all belong to the same component,sayC1.Similarly,the verticesxβ+1,···,xγ−1,uβ+1,···,uγ−1belongtothesamecomponent.SupposethatthisisdiあerentfromC1,sayC2.Also,theverticesxγ+1,···,xα−1,uγ+1,···,uα−1belongtothesamecomponent.SupposethatthisisdiあerentfrombothC1andC2,sayC3.Letthevertices{v0,v1,···,vn−1,y0,y1,···,yn−1}belong to the same component.Suppose that this is diあerent fromC1,C2andC3,sayC4.
SinceSconsists of only outer vertices,which is lie on same outer cycle,then another outer cycle and inner cycles are intact.However,the verticesuiof componentC1,C2andC3all have neighbors in componentC4,wherei∈ {0,1,···,α−1,α+1,···,β−1,β+1,···,γ−1,γ+1,···,n−1}.Thus,the componentC1,C2,C3andC4(even if any two of these component,or all the three component are empty)are connected.In the following,we consider the verticesuα,uβ,uγ.SinceNG−S(uα)={vα−k,vα+k},NG−S(uβ)={vβ−k,vβ+k}andNG−S(uγ)={vγ−k,vγ+k},then,uα,uβanduγare also belongs toC4.Hence,G−Sis connected,a contradiction.
Case 3.2LetS={xα,xβ,yγ},where α,β,γ ∈ {0,1,···,n−1}and α ≠ β.Then,the inner cycles are intact inG−S.
(i)If we suppose thatxαis adjacent toxβthen the outer verticesxβ+1,xβ+2,···,xα−1all lie on a path inG−Sand are adjacent to the corresponding inner verticesuβ+1,uβ+2,···,uα−1.Thus,they all belong to the same component sayC1.Similarly,the verticesyγ+1,yγ+2,···,yγ−1,vγ+1,vγ+2,···,vγ−1belong to the same component.Suppose that this component diあerent fromC1,sayC2.But every inner verticesuihave at least one neighborvjinC2,wherei,j∈ {0,1,···,n−1}andj≠γ,then,uαanduβbelongs toC2.Thus,C1andC2are connected.In the following,we consider the vertexvγ.IfNG(vγ)={yγ,uα,uβ},then sinceuαanduβalso belong toC2,thenvγbelong toC2.If not,vγhave at least one neighbor inC1.Hence,G−Sis connected,contradiction.
(ii)If we suppose thatxαis not adjacent toxβ,then a similar argument to that made from above that the verticesxα+1,···,xβ−1,uα+1,···,uβ−1belong to the same component,sayC1.Similarly,the verticesxβ+1,···,xα−1,uβ+1,···,uα−1belong to the same component.Suppose that this is diあerent fromC1,sayC2.Also,the verticesvγ+1,···,vγ−1,yγ+1,···,yγ−1belong to the same component.Suppose that this is diあerent from bothC1andC2,sayC3.Since every inner verticesuiall have at least one neighborvjinC3,wherei,j∈ {0,1,···,n−1}andj≠ γ.Thus,the componentC1,C2andC3are connected.Then,the verticesuα,uβanduγbelong toC3.Hence,G−Sis connected,a contradiction.
In either case,G−Sis connected,a contradiction.Thus,Case 3 is also not possible.
Hence,|S|≠ 3 and the super-connectivity κ1is at least four.A possible vertex-cut with four vertices that does not create an isolated vertex isS={xα,xα+3,uα+1,uα+3}and thus κ1≤ 4.
The case whenn<2kfollows sinceDP[n,k]is isomorphic toDP[n,n−k].
2 Super-edge-connectivity of DP[n,k]
In this section,we prove that for all values ofn>k,k≥1 andn∉{2k,3},the graphDP[n,k]is super edgeconnected and optimal.We do this by f i rst showing that,providedn∉{2k,3},any edge-cut with cardinality three isolates a vertex.We then exhibit a super edge-cut of cardinality four which disconnectsDP[n,k]without isolating any vertex.
Lemma 2LetG=DP[n,k]forn≥3,k≥1.IfSis an edge-cut ofG,thenScannot be a subset of inner edges.
ProofSuppose thatSconsists of only inner edge andG−Sis disconnected.The outer cycle is intact and each inner vertex is connected to the outer cycle by a spoke,a contradiction.
Since the degree of any vertex inGP[n,k]is three,deleting the three edges incident to a vertex necessary isolates that vertex.Hence,we have the following result.
Lemma 3LetG=DP[n,k]fork≥1,n>kandn≠2k.IfSis a super edge-cut ofG,thenScannot be contain a set of three edges which are incident to the same vertex.
The second theorem in this paper are given in the following.
Theorem 2LetG=DP[n,k]fork≥1 andn>k.The super-edge-connectivity λ1ofGis given by

Furthermore,ifn∉{3,2k},thenGis optimal.
ProofIt is easy to see that ifn=3,then deleting the three spokes incident to the verticesxi(oryi)disconnectsDP[3,k]without isolating a vertex,wherei∈ {0,1,2}andk∈ {1,2}.ThusDP[3,k]is not super-λ.In the double generalized Petersen graphDP[2k,k],the inner vertices generate a union of 2kvertex-disjoint inner edges.Since the deletion of the two spokes adjacent to any inner edge also disconnectsDP[2k,k].Thus,λ(DP[2k,k])=2 andDP[2k,k]is not super-λ.
In the following,we letn>2kandn≠3.Suppose that the super-edge-connectivity λ1is three and letSbe a super edge-cut such that|S|=λ1=3.Thus,G−Sis connected and has no isolated vertices.
In the sequel,forj∈ {0,1,···,n−1},we use the notioneij,eojandesjto denote an inner edge,an outer edge and a spoke,respectively,which is incident to the vertexxj(oryj).Lettis the length of inner cycle ofDP[n,k]andt≥4.
Claim 1Scontains at least one outer edge.
Proof of Claim 1Suppose that the outer cycle is intact.By Lemma 2,Sis one of the following three sets of edges.
Case 1LetS={esα,esβ,esγ}for some α,β,γ ∈ {0,1,···,n− 1},every inner cycle is intact and there aret≥ 4 vertices in each inner cycle.
Case 1.1We suppose f i rst thatSconsists of three spokes,which are incident to the outer verticesxi(yi),wherei,j∈ {0,1,···,n−1}.Since the length of inner cyclet≥ 4,then each inner cycle contains at least two verticesuiandvjwhich are joined by spokes to the outer cycles or outer cycle.We note that this argument holds even if any two of these spokes,or all the three spokes are adjacent to the same inner cycle.Hence,G−Sis connected,a contradiction.
Case 1.2Thus we suppose thatSconsists of two outer spokes and one inner spoke,which are incident to the outer verticesxα,xβand another spoke incident to the outer vertexyγ.Since the length of inner cyclet≥ 4,then each inner cycle contains at least one vertex,which is connected to outer cycles.This argument holds even if any two of these spokes,or all the three spokes are adjacent to the same inner cycle.Since the inner verticesuαanduβhave at least one neighbor ofviandvj,wherei,j≠γ,respectively.Hence,G−Sis connected,a contradiction.
Case 2LetS={eiα,esβ,esγ}for some α,β,γ ∈ {0,1,···,n− 1}.All the inner cycles other than the α-cycle,are intact and the vertices of the α-cycle lie on a pathPt,sayP(1)and the outer cycles are intact.we only need to consider the following two cases.
If we letesγandesβare incident to the outer verticesxγandxβ,respectively.Each of the inner cycles and the pathP(1)havet≥4 vertices.SinceScontains only two spokes(even if any two of these spokes are adjacent to the same inner cycle),each inner cycle and the pathP(1)contain at least two vertices which are connected to the outer cycles,a contradiction.
If we letesβandesγare incident to the outer verticesxβandyγ,respectively.Each of the inner cycles and the pathP(1)havet≥4 vertices.SinceScontains only two spokes(even if any two of these spokes are adjacent to the same inner cycle or these three edges ofSare adjacent),each inner cycles and the pathP(1)contain at least two vertices which are connected to the outer cycles,a contradiction.
Case 3LetS={eiα,eiβ,esγ}for some α,β,γ ∈ {0,1,···,n−1},then the outer cycles are intact.There are two cases to consider as follows.
Ifeiαandeiβare on diあerent inner cycles,then the α-cycle and the β-cycle are distinct.SinceScontains only one spoke,each inner cycle and path contain at least two vertices which are connected to the outer cycle,a contradiction.
Thuseiαandeiβare on the same inner cycle,say the α-cycle.We suppose f i rst that they are not adjacent.In this case,the subgraph induced by the remaining edge of the α-cycle has two components and the number of vertices in each component is greater than or equal to two.SinceShas only one spoke,each component of the α-cycle and each inner cycle is connected to the outer cycles,a contradiction.Suppose thateiαandeiβare adjacent.There is an inner vertex,sayvγ,which is incident to botheiαandeiβ.Since by Lemma 3,esγcannot be incident tovγ,thenvγis connected to the outer cycle.The other vertices of the α-cycle lie on a pathPt−1,sayP(2).SinceSconsists of only one spoke andt≥4,each inner cycle and pathP(2)contain at least one vertex which is connected to the outer cycle,a contradiction.
Claim 2Scontains at least one spoke.
Proof of Claim 2Suppose thatSdose not contain a spoke.By Claim 1,Sis one of the following
Case 1IfS={eoα,eoβ,eoγ}for some α,β,γ ∈ {0,1,···,n− 1},then the inner cycles are intact.SinceDP[n,k]have two outer cycles.First,we suppose thateoα,eoβ,eoγare all incident to the outer verticesxα,xβandxγ,respectively.Then,another outer cycle is intact.Upon deleting three outer edge from the graphG,the subgraph ofG−Sinduced by outer edges has three components and at least one of them hasconsecutive outer vertices.We let this path be in a componentCand note thatthere exist at least one outer vertexxzcontained inC,thenuz∈C,anduz-cycle is intact,thus,the verticesviandyiare all contained inC,wherei∈ {0,1,···,n−1}.This implies that all the outer verticesxiare joined by spoke to the inner cycles.Thus,all the vertices ofG−Sare also in the same componentC,a contradiction.
If the outer edgeseoα,eoβandeoγare lie on diあerent outer cycles,without loss of generality,we leteoαandeoβlie on outer cyclex0x1,···,xα,···,xβ,···,xn−1x0andeoγlie on outer cycley0y1···yγ···yn−1y0.Since every inner cycle is intact,then,all inner vertices are joined by spoke to the outer vertices.Hence,all the vertices ofG−Sare in the same component,a contradiction.
Case 2IfS={eiα,eoβ,eoγ},for some α,β,γ ∈ {0,1,···,n−1}.We suppose fi rst that these two outer edgeseoβandeoγbelongtothesameoutercycle,SinceDP[n,k]havetwooutercycles.Iftheouteredgeseoβandeoγarelieontheouter cyclex0x1,···,xα,···,xβ,···,xn−1x0,then the subgraph ofG−Sinduced by this outer edges has two components and at least one of them haswe let this path be in a componentC.Similarly,the verticesv0,v1,···,vn−1,y0,y1,···,yn−1belong to the same component,suppose that this is diあerent fromC,sayC′.We consider the vertexxz∈C.SinceNG(uz)={xz,vz+k,vz−k},the inner verticesvz+kandvz−kare connected with componentC′.Since all verticesviofC′are joined by inner edge or spokes to the remaining vertices,wherei∈ {0,1,···,n−1},all inner cycles are contained inC,a contradiction.
If the outer edgeseoβandeoγbelong to diあerent outer cycle,then all the remaining outer edges lie on two pathsandrespectively.All the inner cycles,other than the α-cycle,are joined by spokes to the outer vertices.Sincet≥ 4,then,the vertices of α-cycle also joined by spokes to the outer vertices.Hence,G−Sare connected,a contradiction.
Case 3IfS={eiα,eiβ,eoγ}for some α,β,γ ∈ {0,1,···,n−1},then all the inner vertices are connected by spokes to the outer vertices,and the other vertices generate a pathPnand a cycleCninG−S,a contradiction.
We conclude our proof by considering the last three remaining cases.
IfS={esα,eiβ,eoγ}for some α,β,γ ∈ {0,1,···,n−1}.We suppose that the outer edgeeoγincident to the outer vertexxγ.Then the outer verticesxiandyjinG−Slie on a pathPn(sayP(3))andCn,respectively.All the inner cycles other than the β-cycle are intact,and the vertices of the β-cycle generate a pathPt,sayP(4).SinceScontains only one spoke andt≥4,each inner cycle and the pathP(4)contain at least two vertices which are connected to the outer pathP(3)and outer cycleCn,respectively.Hence,G−Sis connected,a contradiction.
IfS={esα,esβ,eoγ},for some α,β,γ ∈ {0,1,···,n−1}.We suppose that the outer edgeeoγincident to the outer vertexxγ,then the outer verticesxiinG−Slie on a pathPn,sayP(5).All the inner cycles are intact and havet≥ 4 vertices.SinceScontains only two spoke,each inner cycle is connected to the outer pathP(5)and outer cycleCn,respectively,a contradiction.
IfS={esα,eoβ,eoγ},for some α,β,γ ∈ {0,1,···,n−1},then the inner cycles remain intact.We suppose f i rst that the two outer edgeseoβ,eoγare incident to a common vertexxz.By Lemma 3,the spokeesαcannot incident toxz,thenxzis connected to an inner cycle.InG−S,all the outer verticesxiexpected forxzlie on a pathPn−1.SinceScontains only one spoke and the outer pathPn−1is connected with at least one vertex of each inner cycle,but the another outer cycleCnofG−Sis intact,then the verticesyiofCnare joined by spoke to inner cycles,a contradiction.Thus the two outer edgeseoβ,eoγare not incident to a common neighbour and the subgraph ofG−Sinduced by the outer edges consists of two paths such that at least one of them hasvertices.We let this path be in a componentC.Then,there must exist a vertexxzin componentC,which joined by spoke to inner cycle.However another outer cycleCnis intact and these verticesyiofCnare adjacent to every inner cycles.Hence,all vertices ofG−Sbelong to the same componentC,a contradiction.
Thus,we can assume that the outer edgeseoβandeoγare lie on diあerent outer cycle,then,the verticesxiandyiofG−Slie on two pathsrespectively.SinceShas only one spoke and all the inner cycles are intact.Then all the inner vertices of inner cycles are joined by spokes to the outer pathPnand outer cycle,respectively.Hence,G−Sis connected,a contradiction.
Thus,|S|≠ 3 and the super-connectivity λ1≥ 4.A possible edge-cut with four edges which does not isolate a vertex is{xα−1xα,xα+1xα+2,xαuα,xα+1uα+2},for α ∈ {0,1,···,n−1}.Thus,λ1=4.
The case whenn<2kfollows sinceDP[n,k]is isomorphic toDP[n,n−k].
References:
[1]Sengupta S,Korobkin C P.Graphs and Digraphs[M].New York:Springer,1994.
[2]Harary F.Conditional connectivity[J].Networks,1983,13(3):347–357.
[3]Coxeter H S M.Self-dual conf i gurations and regular graphs[J].Bulletin of the American Mathematical Society,1950,56(1950):413-455.
[4]Mark E.Watkins.A theorem on tait colorings with an application to the generalized Petersen graphs[J].Journal of Combinatorial Theory,1969,6(2):152-164.
[6]Zhou J X,Feng Y Q.Cubic Vertex-Transitive Non-Cayley Graphs of Order 8p[J].Electronic Journal of Combinatorics,2012,19(1):453-472.
[6]Zhou J X,Feng Y Q.Cubic bi-Cayley graphs over abelian groups[J].European Journal of Combinatorics,2014,36(2):679-693.
[7]Boesch F,Tindell R.Circulants and their connectivities[J].Journal of Graph Theory,2010,8(4):487-499.
[8]Yang W H,Meng J X.Extraconnectivity of hypercubes(II)[J].Australas Journal of Combinatorics,2010,47:189-195.
[9]Ekinci G B,Kırlangic¸A.Super connectivity of Kronecker product of complete bipartite graphs and complete graphs[J].Discrete Mathematics,2016,339(7):1950-1953.
[10]Min L,Chao W,Chen G,et al.On super connectivity of Cartesian product graphs[J].Networks,2010,52(2):78-87.
[11]Ferrero D,Hanusch S.Component connectivity of generalized Petersen graphs[J].International Journal of Computer Mathematics,2014,91(9):1940-1963.
[12]BoruzanlıEkinciG,GauciJB.OnthereliabilityofgeneralizedPetersengraphs[J].DiscreteAppliedMathematics,[2017-02-24],https://doi.org/10.1016/j.dam.2017.02.002.
[13]Kutnar K,Petecki P.On automorphisms and structural properties of double generalized Petersen graphs[J].Discrete Mathematics,2016,339(12):2861-2870.

